题目描述

汤姆斯生活在一个等级为 $0$ 的星球上。那里的环境极其恶劣，每天 $12$ 小时的工作和成堆的垃圾让人忍无可忍。他向往着等级为 $N$ 的星球上天堂般的生活。

有一些航班将人从低等级的星球送上高一级的星球，有时需要向驾驶员支付一定金额的费用，有时却又可以得到一定的金钱。

汤姆斯预先知道了从 $0$ 等级星球去 $N$ 等级星球所有的航线和需要支付（或者可以得到）的金钱，他想寻找一条价格最低（甚至获得金钱最多）的航线。

输入格式

第一行一个正整数 $N$（$N\le 100$），接下来的数据可分为 $N$ 个段落，每段的第一行一个整数 $K_i$（$K_i\le 100$），表示等级为 $i$ 的星球有 $K_i$ 个。

接下来的 $K_i$ 行中第 $j$ 行依次表示与等级为 $i$，编号为 $j$ 的星球相连的等级为 $i-1$ 的星球的编号和此航线需要的费用（正数表示支出，负数表示收益，费用的绝对值不超过 $1000$）。

每行以 $0$ 结束，每行的航线数 $\le 100$。

输出格式

输出所需（或所得）费用。正数表示支出，负数表示收益。

样例 #1

样例输入 #1

3
2
1 15 0
1 5 0
3
1 -5 2 10 0
1 3 0
2 40 0
2
1 1 2 5 3 -5 0
2 -19 3 -20 0

样例输出 #1

-1

提示

对于 $100\%$ 的数据，$1\le N\le 100$，$1\le K_i\le 100$。

样例解释：

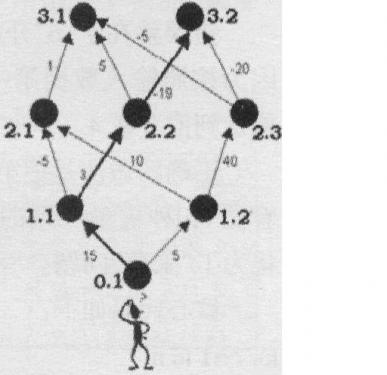
解题思路：

先介绍一下Dijkstra思想（已经了解可以跳过）

其实质是贪心

Dijkstra将所有点划分为两个点集

其中最短路径集里所有点的最短路径均是已知的

最初，所有的点均属于非最短路径集

首先将起点加入到最短路径集

然后尝试从起点能够到达的所有点

将其中路径最短的点加入到最短路径集，然后尝试从新的点能够到达的所有点

再次把已尝试过所有路径中路径最短的点加入最短路径集，然后循环上述步骤

注意，是尝试过的所有路径中，而不是第二次尝试的路径中

单源最短路径，可以想到使用Dijkstra，但鉴于输入数据的特殊性，还需要做一些处理

首先，注意到本题每个节点是由等级和编号唯一确定的

但是我们仍可将其抽象为唯一的编号，如样例中的点可以标号为$1$~$8$

然后，注意到本题中的边权可能为负数，要知道Dijkstra中的边权不能为负

把所有边权整体加上一个偏移量即可

那么存图的问题解决了，接下来就是套用Dijkstra算法了

AC代码如下

#include <iostream>
#include <vector>
#include <queue>
#include <memory.h>
using namespace std;
const int max_n = 100;
const int max_k = 100;
const int max_m = 100;
const int NaN = 0x3F3F3F3F;

class greater_queue {
public:
	bool operator()(pair<int, int>p_1, pair<int, int>p_2) {
		return p_1.first > p_2.first;
	}
};

priority_queue<pair<int, int>, vector<pair<int, int>>, greater_queue>p_q;
struct edge { int v, p, next; }edges[max_n * max_k * max_m];//链式前向星
int head[max_n * max_k + 2] = { -1 };
int tot = -1;
int min_dist[max_n * max_k + 2] = { NaN };
bool book[max_n * max_k + 2] = { false };//最短路径集

void add_edge(int u, int v, int p) {//存图
	edges[++tot] = { v,p,head[u] }; head[u] = tot;
}

void dijkstra() {
	min_dist[1] = 0;
	p_q.push(pair<int, int>(0, 1));//初始化

	while (!p_q.empty()) {
		int node = p_q.top().second;
		int dist = p_q.top().first;
		p_q.pop();

		if (book[node]) continue;//已加入最短路径集
		book[node] = true;//未加入最短路径集

		for (int i = head[node]; i != -1; i = edges[i].next) {//尝试更新最短路径
			int v = edges[i].v;
			if (min_dist[v] > edges[i].p + dist) {
				min_dist[v] = edges[i].p + dist;
				p_q.push(pair<int, int>(min_dist[v], v));
			}
		}
	}
}

int main() {
	memset(head + 1, -1, sizeof(int) * (max_n * max_k + 1));
	memset(min_dist + 1, 0x3F, sizeof(int) * (max_n * max_k + 1));//初始化
	int n, k, u, p, cur_tot = 1, temp_tot = 0;
	cin >> n;
	for (int i = 1; i <= n; i++) {//存图
		cin >> k;
		for (int j = 1; j <= k; j++) {
			++cur_tot;//节点分配
			while (true) {
				cin >> u;
				if (u == 0) break;//行尾
				cin >> p;
				add_edge(temp_tot + u, cur_tot, p + 1000);//边权偏移
			}
		}
		temp_tot = cur_tot - k;//寻访i-1级星球
	}

	dijkstra();

	int ans = NaN;
	for (int i = temp_tot + 1; i <= cur_tot; i++) {//寻找最小值
		ans = min(ans, min_dist[i]);
	}
	cout << ans - 1000 * n << endl;//平衡偏移、输出
	return 0;
}