一、实验目的
1. 熟悉启动和退出 MATLAB 的方法。
2. 熟悉 MATLAB 命令窗口的组成。
3. 掌握 MATLAB 基本绘图函数和图像处理函数的使用。
4. 掌握图像内插和灰度图像的集合运算。
二、实验例题
1. 求下列表达式的值
(1)
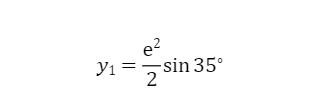
(2)
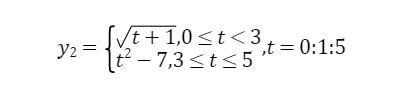
答:
(1)
y1=exp(2)/2*sin(35*pi/180)y1 =
2.1191
(2)
方法 1:用逻辑表达式
t=0:1:5;
y2=(0<=t&t<3).*sqrt(t+1)+(3<=t&t<=5).*(t.^2-7)
%或者 y2=(t>=0&t<3).* sqrt(t+1)+(t>=3&t<=5).*(t.^2-7)y2 =
1.0000 1.4142 1.7321 2.0000 9.0000 18.0000
方法 2:用循环结构和选择结构
y2=[]; i=0;
for t=0:1:5;
if 0<=t&t<3
y= sqrt(t+1);
else 3<=t&t<=5
y=t^2-7;
end
i=i+1;
y2(i)=y;
end
y2y2 =
1.0000 1.4142 1.7321 2.0000 9.0000 18.0000
2. find 函数和空矩阵的使用
找出字符串 abscdsesfs 中的‘s’所在的位置并计数,然后求将所有‘s’删除后的字符串。
答:
str='abscdsesfs';
k=find(str>'r'&str<'t')k =
3 6 8 10
length(k)ans =
4
str(k)=[];
strstr =
abcdef
3. 基本图像处理函数的使用
(1) 读入和显示图像。读入图 1 所示的 Peppers 图像,并使用 imshow 函数将其显示出来。(当要用 imshow 显示另一幅图像时, MATLAB 会用新图像替换旧图像,为保持第一幅图像并同时显示第二幅图像,可使用 figure 函数,如(3)中的代码所示)。
(2) 保存图像。将图 1 的图像保存成 bmp 格式的 Peppers。 MATLAB 中函数 imread 和imwrite所支持的一些常用图像/图形格式如表 1 所示。
表 1 MATLAB 中函数 imread 和 imwrite 所支持的一些常用图像/图形格式
格式名称 | 描述 | 可识别扩展符 |
TIFF | 加标识的图像文件格式 | .tif, .tiff |
JPEG | 联合图像专家组 | .jpg, .jpeg |
GIF | 图形交换格式 | .gif |
BMP | Windows 位图 | .bmp |
PNG | 可移植网络图像 | .png |
XWD | X Window 转储 | .xwd |
(3) 用函数 rgb2gray 将图 1 所示的彩色图像转换成灰度图像。
(4) 用 imhist 函数绘制灰度图像的直方图。
(5) 图像窗口分割。用函数 subplot,将图像窗口分割成布局,在第一个窗口中显示
原始的 Peppers 图像,在第二个窗口显示其灰度图像。
(6) 图像翻转。将 Peppers 的灰度图像进行上下翻转。

图1 Peppers图像
答:
(1)
f=imread('例 3.Peppers.tiff');
imshow(f)(2)
imwrite(f,'Peppers02.bmp')(3)
g=rgb2gray(f);
figure; imshow(g)
(4)
imhist(g)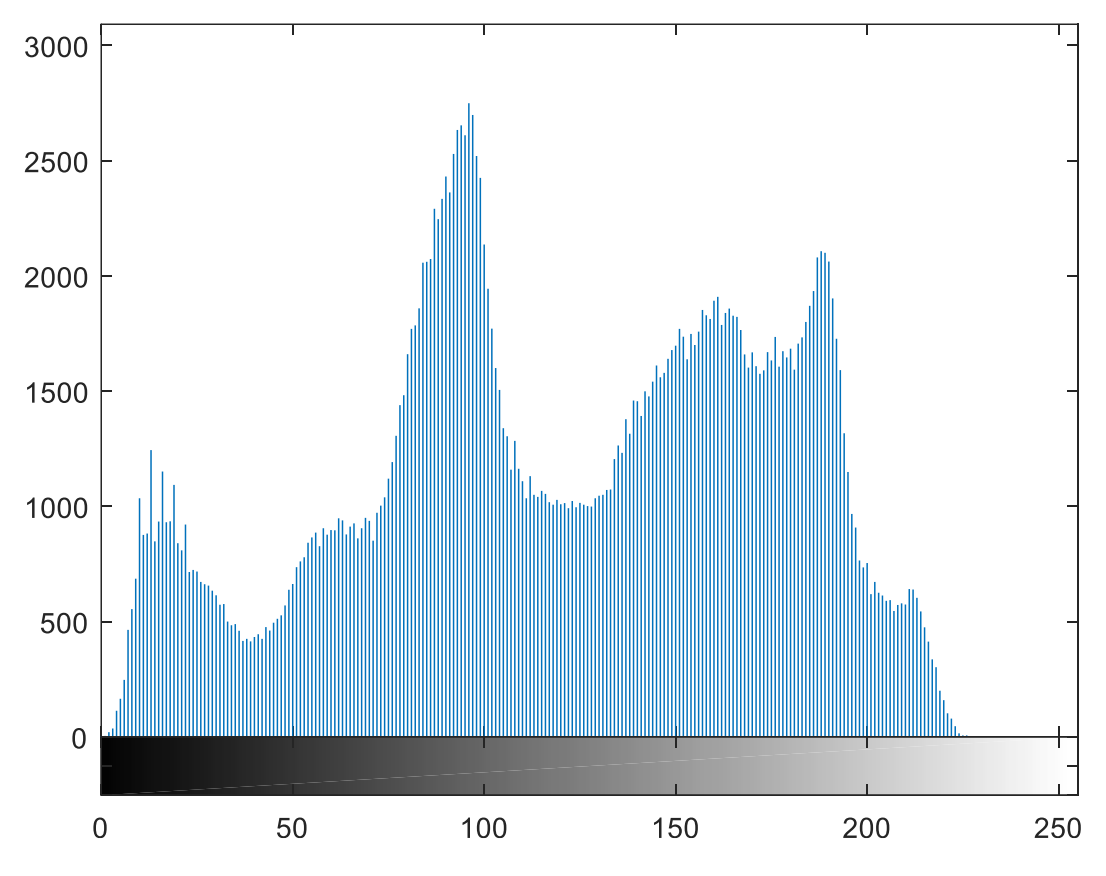
(5)
subplot(1,2,1)
imshow(f);
subplot(1,2,2)
imshow(g);
(6)
g1=g(end:-1:1,:);
figure; imshow(g1);4. 曲线的绘制
色彩、点型与线型的设置在很多情况下,为在同一个图像窗口中展示不同的信息,我们需要设置不同属性的曲线,例如不同的色彩、数据点型以及线型。绘图指令的颜色、点型和线型的相关参数如表 2 所示。
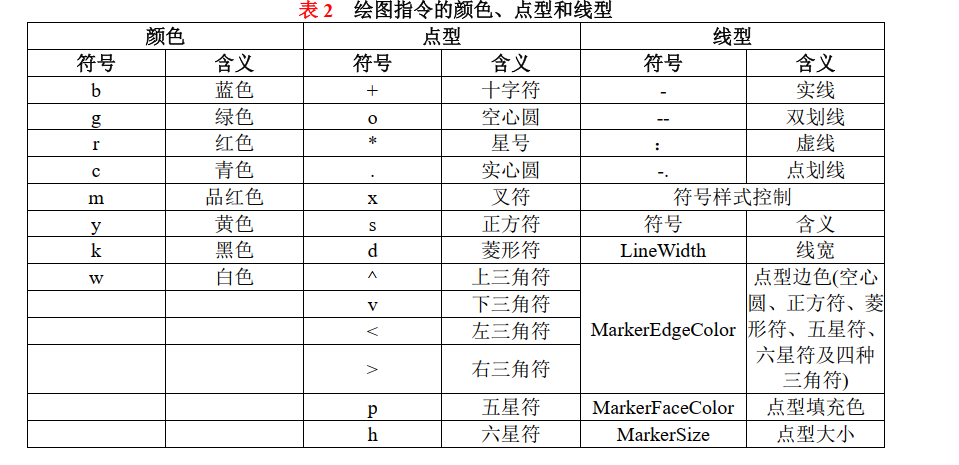
绘图指令参量由线型符号、色彩符号和点型符号中各选一个符号组合而成,也可以由其中的一项或多项组成, 没有先后顺序。
练习:
(1) 用 plot 函数,在同一个图像窗口中绘制函数和 ,将曲线的色彩设置为红色,线型设置为实线,点型为十字符; 将曲线的色彩设置为蓝色,线型为虚线,点型为空心圆。 设置坐标轴刻度为“Times New Roman”,字号 12 磅。
(2) 设置标题为“余弦函数和正弦函数”, 设置图例为“”和“ ”, 标注 x 轴和 y 轴,中文字体为“宋体”,英文为“Times New Roman”,字号 12 磅。 注意,变量 x 和 y 标注时为斜体。
答:
(1)
x=0:pi/10:2*pi;
y1=cos(x);
y2=sin(x);
plot(x,y1,'-r+');
hold on
plot(x,y2,':bo');
hold off
set(gca,'Fontname', 'Times New Roman', 'FontSize',12);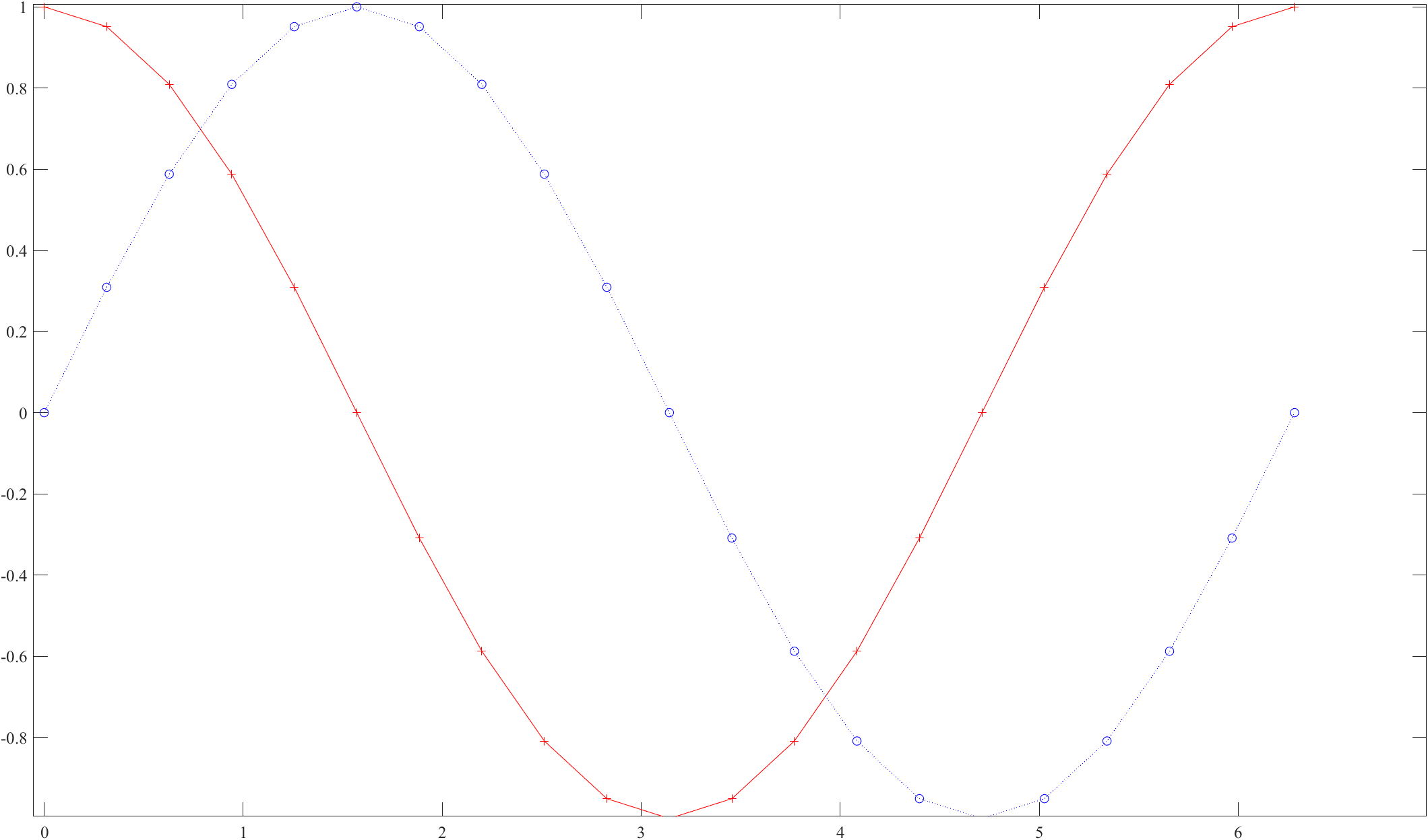
(2)
title('\fontname{宋体}余弦函数和正弦函数','FontSize',12);
legend('\ity\rm_1', '\ity\rm_2')
xlabel('\fontname{Times New Roman}{\itx }\fontname{宋体}轴', 'FontSize',12);
ylabel('\fontname{Times New Roman}{\ity }\fontname{宋体}轴', 'FontSize',12);
% \rm 转变为罗马族,直立形状,中等粗细系列的字体属性,这是默认的字体
% \it 转变为罗马族,斜体形状,中等粗细系列的字体属性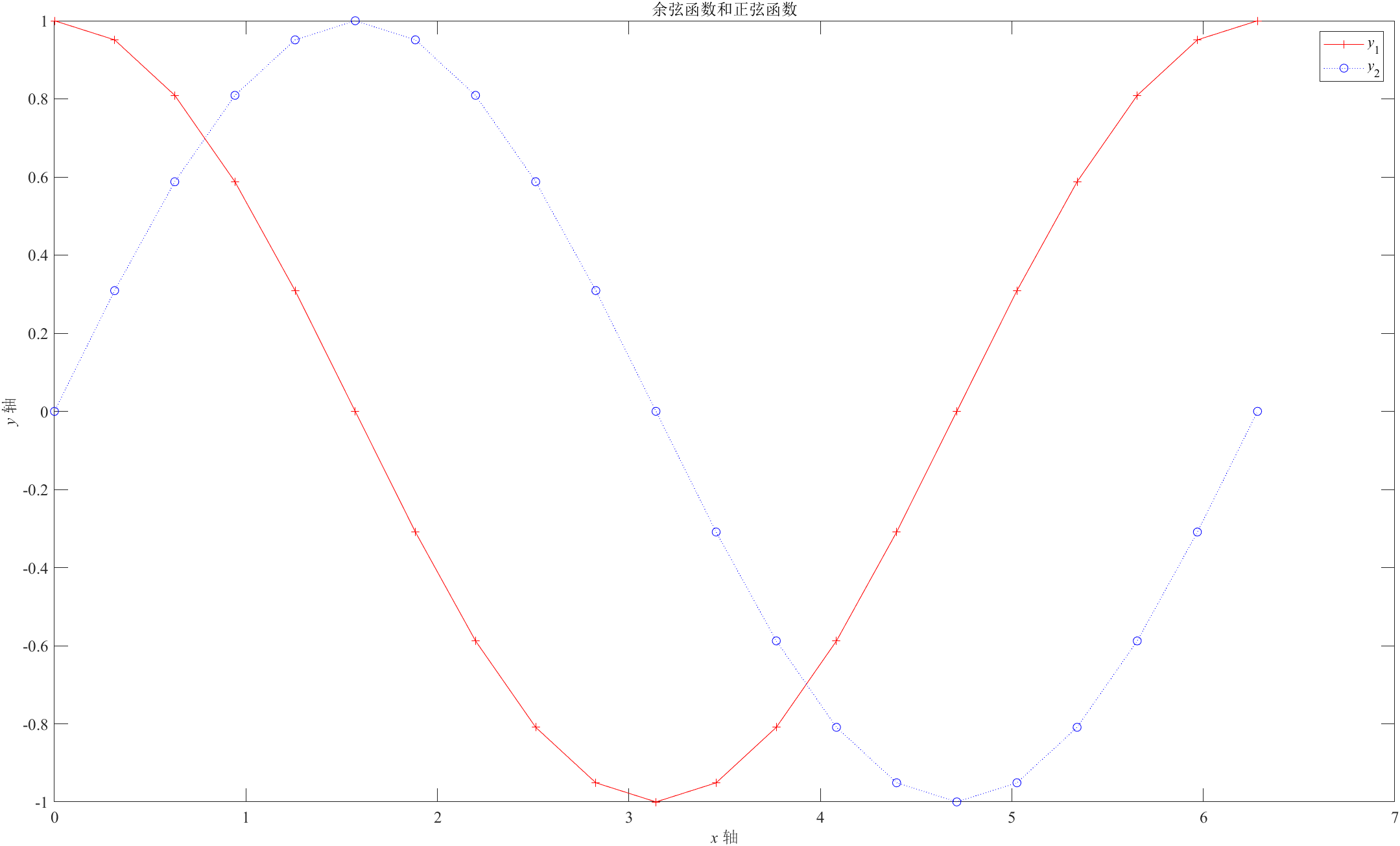
5. 图像内插
图像内插由工具箱中的函数 interp2 实现,该函数的语法为:
ZI = interp2(X, Y, Z, XI, YI, method)其中, ZI 是对 X、 Y 和 Z 定义的二维数组进行对应于 XI 和 YI 的内插运算的返回数组,默认 X = 1:n、 Y = 1:m,这里[m, n] = size(Z)。 参数 method 定义了选择内插的方法,可选的方法包括:
(1) ‘nearest’: 最近邻内插;
(2) ‘linear’: 双线性内插(默认);
(3) ‘spline’: 三次样条内插;
(4) ‘cubic’: 双三次内插。
练习:
图 2 给出了一幅大小为 165×166 的图像,其原来的大小为 2136×2140。请分别用最近邻内插、双线性内插和双三次内插这三种方法,将图 2 的图像放大到原来的大小。

图2 内插实验
答:
clear all; close all; clc;
f = imread('例 5.内插实验.tif');
f = double(f);
[X,Y]=meshgrid(0:165,0:164);
[XI,YI]=meshgrid(0:165/2139:165,0:164/2135:164);
ZI1 = interp2(X, Y, f, XI, YI, 'nearest');
figure; imshow(ZI1,[]);
ZI2 = interp2(X, Y, f, XI, YI, 'linear');
figure; imshow(ZI2,[]);
ZI3 = interp2(X, Y, f, XI, YI, 'cubic');
figure; imshow(ZI3,[]);
最邻近内插

双线性内插

双三次内插