7-1 最小路径和
给定一个m行n列的矩阵,从左上角开始每次只能向右或者向下移动,最后到达右下角的位置,路径上的所有数字累加起来作为这条路径的和。求矩阵的最小路径和。
输入格式:
输入第一行:两个正整数m和n(1<=m, n<=1000),以空格隔开,为矩阵的行数和列数;接下来m行,每行n个整数,为给定的矩阵。
输出格式:
输出只有一行:一个整数,为矩阵的最小路径和。
输入样例:
4 4
1 3 5 9
8 1 3 4
5 0 6 1
8 8 4 0输出样例:
12提示:
1、可记dp(i,j)由左上角开始到达i行j列后的最小路径和,则dp(m,n)为所求。
2、请参考教材:"8.4 求解三角形最小路径问题"的示例。
如果不采用动态规划法,本题不得分!
思路:
数字三角形dp模型 状态转移方程
AC代码:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e3 + 7;
int n, m;
int g[N][N], f[N][N];
int main() {
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> g[i][j];
}
}
f[1][1] = g[1][1];
for (int i = 2; i <= n; i++) f[i][1] = f[i - 1][1] + g[i][1]; //第一列边界
for (int i = 2; i <= m; i++) f[1][i] = f[1][i - 1] + g[1][i]; //第一行边界
for (int i = 2; i <= n; i++) {
for (int j = 2; j <= m; j++) {
f[i][j] = g[i][j] + min(f[i][j - 1], f[i - 1][j]);
}
}
cout << f[n][m] << endl;
return 0;
}7-2 袋鼠过河
一只袋鼠要从河这边跳到河对岸,河很宽,但是河中间打了很多桩子,每隔1米就有1个,第一个桩子就打在河岸边,对岸的岸边没有桩子,如下图:
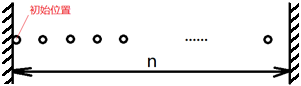
每个桩子上有一个弹簧,袋鼠跳到弹簧上就可以跳的更远。每个弹簧力量不同,用一个数字代表它的力量,如果弹簧的力量是5,就表示袋鼠下一跳最多能跳5米,如果是0,就表示会陷进去无法继续跳跃。河流一共n米宽,袋鼠初始在第一个弹簧上面,给定每个弹簧的力量,求袋鼠最少需要多少跳能够到达对岸。如果无法到达,输出-1。
输入格式:
输入包括两行,第1行为河的宽度n(1<=n<=10000),第2行为n个整数ai(0<=ai<=20,且ai<n),表示每个弹簧的力量,用空格隔开。
输出格式:
输出到达对岸的最少跳数,若无法到达,输出-1。
输入样例1:
5
2 0 1 1 1输出样例1:
4输入样例2:
5
2 3 1 0 1输出样例2:
3输入样例3:
5
2 0 0 8 1输出样例3:
-1提示:
1、可假想在对岸的岸边也有一个桩子,从初始位置开始给这些桩子编号,(假设从0开始编)则编号范围为0~n,记dp(i)为到达编号为i的桩子的最少跳数,则dp(n)为所求。
2、如果不采用动态规划法,本题不得分!
AC代码:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e3 + 7, inf = 0x3f3f3f3f;
int n, m;
int f[N], a[N];
//类似于求最长上升子序列问题
//f[i]表示袋鼠到达第i个弹簧上的最少跳数
//因为我们要走到对岸 假设对岸也有一个弹簧 因此最后答案就是 f[n + 1]
int main() {
ios::sync_with_stdio(false);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
memset(f, 0x3f, sizeof f);
f[1] = 0; //初始化第一个弹簧时跳数
for (int i = 2; i <= n + 1; i++) {
for (int j = 1; j <= i; j++) {
if (a[j] + j >= i) //每次遍历前面的数看是否能够到达当前位置
f[i] = min(f[i], f[j] + 1);
}
}
if (f[n + 1] == inf) cout << -1;
else cout << f[n + 1];
return 0;
}题目来源:搜狐2017秋招研发工程师笔试-袋鼠过河
7-3 数字和
给定一个有n个正整数的数组a和一个整数sum,求选择数组a中的部分数字和为sum的方案数。若两种选取方案有一个数字的下标不一样,则认为是不同的方案。
输入格式:
输入包括两行,第1行为两个正整数n和sum(1<=n, sum<=1000),第2行为n个正整数ai(32位整数),并以空格隔开。
输出格式:
输出所求的方案数。
输入样例:
5 15
5 5 10 2 3输出样例:
4提示:
1、可记dp(i,j)为处理完前i个数字后,选取的数字和为j的方案数,则dp(n,sum)为所求。
2、特别注意:若i为0,即无数字可选,则只要j≠0,方案数均为0;若j为0,则无论i为何值,均有一种方案可选,即空集。
3、如果不采用动态规划法,本题不得分!
思路:
背包问题求解方案数 注意开long long
状态转移方程:
AC代码
#include <iostream>
#include <cstring>
#define int long long
using namespace std;
const int N = 1e3 + 7, mod = 1e9 + 7;
int n, m;
int f[N], a[N];
signed main() {
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
f[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = m; j >= a[i]; j--) {
f[j] += f[j - a[i]];
}
}
cout << f[m] << endl;
return 0;
}7-4 买股票
“低价购买”这条建议是在股票市场取得成功的一半规则。要想被认为是伟大的投资者,你必须遵循以下的问题建议:“低价购买;再低价购买”。每次你购买一支股票,必须用低于你上次购买它的价格购买它。买的次数越多越好!你的目标是在遵循以上建议的前提下,求出最多能购买股票的次数。题目给出一段时间内一支股票每天的出售价,你可以选择在哪些天购买这支股票。每次购买都必须遵循“低价购买;再低价购买”的原则。写一个程序计算最大购买次数。
例如,这里是某支股票的价格清单:
日期:1,2,3,4,5,6,7,8,9,10,11,12
价格:68,69,54,64,68,64,70,67,78,62,98,87
最优秀的投资者可以购买最多4次股票,可行方案中的一种是:
日期:2,5,6,10
价格:69,68,64,62
输入格式:
输入包含多个样例,每个输入样例:
第1行: N(1<=N<=5000),股票发行天数
第2行: N个数,是每天的股票价格(216范围内的正整数)。
输出格式:
对应每个输入样例,输出1行,1个整数:最大购买次数。
输入样例:
12
68 69 54 64 68 64 70 67 78 62 98 87
20
157 27 28 100 48 199 10 128 189 151 146 170 188 64 199 156 84 182 19 125输出样例:
4
6提示:
1、最长单调递减子序列问题;
2、如果不采用动态规划法,本题不得分!
AC代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long
using namespace std;
const int N = 1e3 + 7, mod = 1e9 + 7;
int n, m, res;
int f[N], a[N];
signed main() {
ios::sync_with_stdio(false);
while (cin >> n) {
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = n; i >= 1; i--) {
f[i] = 1;
for (int j = n; j > i; j--)
if (a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
cout << res << endl;
}
return 0;
}7-5 愤怒的小鸟
游戏"愤怒的小鸟",各位仙家都玩过了吧,俗话说:“飞得越高,砸得更狠”,各小鸟们在游戏中简直是各显神通,竞相飞得更高,哪怕是粉身碎骨,但求美名留人间。
为了获得更高的飞越高度,小鸟们不知从何处得到了一批神力大补丸,吃了这些大补丸将可以帮助小鸟们获得更高的飞行高度。不幸的是,不知道那个该死的叛徒走漏了消息,可恶的绿猪获得了这个情报,于是他们贿赂了当地的一个巫师,希望巫师从中作梗为难小鸟们,于是巫师连夜在这批大补丸上施加了一种可怕的诅咒,就是小鸟们在服用这些大补丸时,当吃到奇数个大补丸会增加飞行功力(增加值为该大补丸的“药力”值);吃到偶数个大补丸会降低飞行功力(降低值也是该大补丸的“药力”值),当然小鸟们在挑选时可以跳过某些大补丸不吃。小鸟们有点犯难,虽然说只要谨慎挑选是可以确保吃了这批大补丸后能得到功力的提升,但挑选不当也可能会导致功力的降低,因此绝不可以随便处理了事,更何况神力大补丸之所以称为神力,那可是花了高价钱好不容易才搞到手的。有没有一种选择方案可以让这批神力大补丸发挥最大的药效呢?
幸好,小鸟们有个当程序员的朋友,也就是你,他们现在求助于你,那么你能找到一种选择方案可以让这批神力大补丸发挥最大的药效吗?
注:场景设计原创,转载请标明出处!
输入格式:
输入有多组用例,对每组用例:
第1行:一个整数n(1<=n<=150,000),表示大补丸的数量
第2行:包含n个整数pi(1<=pi<=500),每个整数表示一个大补丸的“药力”值。假设小鸟们只能按这个给定的次序依次挑选大补丸。
输出格式:
对应每个输入样例,输出1行:一个整数,食用这批神力大补丸后能达到的最大的药效。
输入样例:
8
7 2 1 8 4 3 5 6
12
51 141 41 152 79 72 28 145 41 26 176 78输出样例:
17
519提示:
样例解释:第1个样例,依次取7,1,8,3,6,最大的药效=7-1+8-3+6=17;第2个样例,依次取141,41,152,28,145,26,176,最大的药效=141-41+152-28 +145-26+176=519。
1、思路:可分别标记处理完第i个大补丸后,当前拿到的是偶数个大补丸或者是奇数个大补丸的最优值,再考虑上一个状态如何到达这个状态。最终解为处理完最后一个大补丸后,当前是偶数个大补丸的最优值和当前是奇数个大补丸的最优值的较大值。
如果不采用动态规划法,本题不得分!
AC代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5 + 7, mod = 1e9 + 7;
int n, m, res;
int f[N], a[N];
signed main() {
ios::sync_with_stdio(false);
while (cin >> n) {
for (int i = 1; i <= n; i++) cin >> a[i];
int k = 1; //k种状态
for (int i = 1; i <= n; i++) {
if (k & 1) { //奇数时
if (a[i] > a[i + 1])
f[k] = f[k - 1] + a[i], k ++;
}
else { //偶数时
if (a[i] < a[i + 1])
f[k] = f[k - 1] - a[i], k++;
}
}
cout << f[k - 1] << endl;
}
return 0;
}7-6 矩阵连乘问题
给定n个矩阵A1,A2,…,An,其中,Ai与Aj+1是可乘的,i=1,2,…,n-1。
你的任务是要确定矩阵连乘的运算次序,使计算这n个矩阵的连乘积A1A2…An时总的元素乘法次数达到最少。
例如:3个矩阵A1,A2,A3,阶分别为10×100、100×5、5×50,计算连乘积A1A2A3时按(A1A2)A3所需的元素乘法次数达到最少,为7500次。
输入格式:
测试数据有若干组,每组测试数据有2行。
每组测试数据的第1行是一个整数n(1<=n<=100),第2行是n+1个正整数p0、p1、p2、…、pn,这些整数不超过100,相邻两个整数之间空一格,他们表示n个矩阵A1,A2,…,An的阶pi−1×pi,i=1,2,…,n。
输出格式:
对输入中的每组测试数据,输出2行。先在一行上输出“Case #”,其中“#”是测试数据的组号(从1开始),再在第2行上输出计算这n个矩阵的连乘积A1,A2,…,An时最少的总的元素乘法次数。
输入样例:
3
10 100 5 50
4
50 10 40 30 5输出样例:
Case 1:
7500
Case 2:
10500提示:
1、分析最优解的结构:
设计求解具体问题的动态规划算法的第一步是刻画该问题的最优解的结构特征。我们将矩阵连乘积AiAi+1....Aj简记为A[i:j]。考察计算A[1:n]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开,1<=k<n,则其相应的完全加括号形式为((A1...Ak)(Ak+1...An))。以此次序,总的计算量为A[1:k]的计算量加上A[k+1:n]的计算量, 再加上A[1:k]和A[k+1:n]相乘的计算量。
这个问题的关键特征是:计算A[1:n]的最优次序所包含的计算矩阵子链A[1:k]和A[k+1:n]的次序也是最优的。因此,矩阵连乘积计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。问题的最优子结构性质是该问题可以用动态规划算法求解的显著特征。
建立递归关系
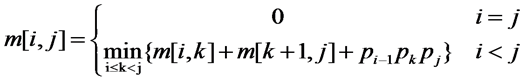
从连乘矩阵个数为2开始计算每次的最小乘次数:m[0][1]、m[1][2]、m[2][3]、m[3][4]、m[4][5],其中m[0][1]表示第一个矩阵与第二个矩阵的最小乘次数;
然后再计算再依次计算连乘矩阵个数为3的最小乘次数:m[0][2]、m[1][3]、m[2][4]、m[3][5];
连乘矩阵个数为4的最小乘次数:m[0][3]、m[1][4]、m[2][5]
连乘矩阵个数为5的最小乘次数:m[0][4]、m[1][5]
连乘矩阵个数为6的最小乘次数:m[0][5],这个是最后我们要的结果。
m[i][j]给出了最优值,即计算A[i:j]所需的最少数乘次数。同时还确定了计算A[i:j]的最优次序中的断开位置k,也就是说,对于这个k有:
m[i][j]=m[i][k]+m[k+1][j] + Pi−1∗Pk∗Pj
若将对应于m[i][j]的断开位置k记为s[i][j],在计算最优值m[i][j]后,可以递归地有s[i][j]构造出相应的最优解。
计算最优值
根据计算m[i][j]的递归式,容易写一个递归算法计算m[1][n]。但是简单地递归将好费指数计算时间。在递归计算时,许多子问题被重复计算多次。这也是该问题可以用动态规划算法求解的又一显著特征。
用动态规划算法解决此问题,可依据其递归是以自底向上的方式进行计算。在计算的过程中,保存以解决的子问题答案。每个子问题只计算一次,而在后面需要时只要简单查一下,从而避免大量的重复计算。
4、如果不采用动态规划法,本题不得分!
AC代码:
#include <iostream>
#include <cstring>
const int N = 1e2 + 7;
int p[N], n;
int m[N][N], s[N][N];
using namespace std;
int MatrixChain(int n) {
for (int i = 1; i <= n; i++) {
//矩阵链中只有一个矩阵时,次数为0,注意m[0][X]是不用的!
m[i][i] = 0;
}
for (int r = 2; r <= n; r++) { //矩阵链长度,从长度为2开始
//根据链长度,控制链最大的可起始点
for (int i = 1; i <= n - r + 1; i++) {
//矩阵链的末尾矩阵,注意r-1,因为矩阵链为2时,实际是往右+1
int j = i + (r - 1);
//先设置最好的划分方法就是直接右边开刀,后续改正,也可合并
//到下面的for循环中
m[i][j] = m[i][i] + m[i + 1][j] + p[i - 1] * p[i] * p[j];
s[i][j] = i;
//这里面将断链点从i+1开始,可以断链的点直到j-1为止
for (int k = i + 1; k < j; k++) {
int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if (t < m[i][j]) {
m[i][j] = t;
s[i][j] = k;
}
}
}
}
return m[1][n];
}
//追踪函数:根据输入的i,j限定需要获取的矩阵链的始末位置,s存储断链点
void Traceback(int i, int j) {
if (i == j) { //回归条件
printf("A%d", i);
} else { //按照最佳断点一分为二,接着继续递归
printf("(");
Traceback(i, s[i][j]);
Traceback(s[i][j] + 1, j);
printf(")");
}
}
int main() {
while (~scanf("%d", &n)) {
memset(p, 0, sizeof(p));
memset(m, 0, sizeof(m));
memset(s, 0, sizeof(s));
for (int i = 0; i <= n; i++) scanf("%d", &p[i]);
printf("%d\n", MatrixChain(n));
//Traceback(1,n);
}
return 0;
}7-7 极速滑雪
北京冬奥会开赛在即,想体验一下什么是速度与激情吗?那么你应该了解一个叫做极速滑雪的运动,这个运动绝对是惊险与刺激的完美结合,需要足够的勇气与胆量!滑雪开始时,必须选择一个制高点然后向低处滑,到下一个位置继续选择一个较低的位置往下滑…,如果每次选择的位置极佳,将会获得最快的滑行速度以及最长的滑行长度。但如果不幸滑入一个洼地(四周位置都高于当前所处的位置),那么将不得不结束比赛并且最终成绩为总的滑行长度。赛事的评价标准很简单,就是谁的滑行长度最长,冠军就将花落谁家。现在,你的任务就是帮助选手找到一条最长的滑行赛道!
滑雪区域将由一个二维数组给出,数组元素的值代表每个位置的高度值。下面是一个例子:
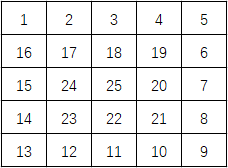
每个选手可以从某个位置滑向东南西北相邻四个位置之一,并且必须高度减小(即不能向上滑)。在上面的例子中,一条可滑行的赛道为24-17-16-1(长度=4);当然25-24-23-...-3-2-1(长度=25)更长,事实上,这是最长的一条,如下图所示:
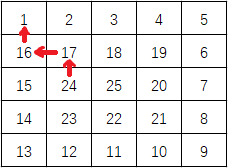
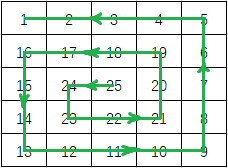
注:场景设计原创,转载请标明出处!
输入格式:
输入的第一行包括空格隔开的两个整数,表示滑雪区域的行数R和列数C(1 <= R,C <= 100)。下面是R行,每行有空格隔开的C个整数,代表高度h(0<=h<=10000)。
输出格式:
输出最长的滑行赛道的长度。
输入样例:
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9输出样例:
25提示:
1、思路:高度排序,从最低位置开始循环更新其四周四个位置的赛道长度(假设当前位置四周的某个位置为i,若i的高度比当前位置高,且以i为起点的赛道长度<以当前位置为起点的赛道长度+1,则以i为起点的赛道长度=以当前位置为起点的赛道长度+1),max{以位置j为起点的赛道长度}为所求,其中1≤j≤R*C。
2、如果不采用动态规划法,本题不得分!
思路:记忆化搜索
AC代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e2 + 7;
int n, m;
int g[N][N], f[N][N];
int dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, 0};
int dfs(int x, int y) {
if (f[x][y] != -1) return f[x][y];
f[x][y] = 1; //初始化1
for (int i = 0; i < 4; i++) {
int a = x + dx[i], b = y + dy[i];
if (a < 1 || a > n || b < 1 || b > m) continue; //判断边界
if (g[a][b] >= g[x][y]) continue; //只能从高往低滑 相等情况也不行
f[x][y] = max(f[x][y], dfs(a, b) + 1);
}
return f[x][y];
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> g[i][j];
}
}
int res = 0;
memset(f, -1, sizeof f); //不为-1就是已经计算过了 搜索过程中遇到直接返回
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
res = max(res, dfs(i, j));
}
}
cout << res << endl;
return 0;
}