子串
560.和为K的子数组
使用前缀和预处理一下题目给的数组, 然后用二重循环遍历一遍就可以了。
239.滑动窗口最大值
看题面比较容易想到的是用优先级队列来解决, 但是STL中的priority_queue不支持随机删除, 如果要用优先级队列来解决这道题的话比较复杂。这道题的一种正确解法是用单调队列来处理, 单调队列专门用来处理类似滑动窗口的区间最值问题。
接下来来看针对这道题, 单调队列是如何处理元素的入队和出队呢?
- 入队: 从队列的后方入队, 弹出所有比当前元素(即待入队元素)小的元素, 因为这些元素都比当前元素小, 而且入队时间更早, 如果队列中有当前元素, 那么这些较小的元素永远不可能成为答案
- 出队: 从队列的前方出队, 先弹出所有已经在区间外的元素, 然后得到的队头即是当前窗口的最大值
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> res;
deque<int> que; // 出队从前面, 入队从后面
for (int i = 0; i < k; ++i) {
while(!que.empty() && nums[i] > nums[que.back()]) que.pop_back();
que.push_back(i);
}
res.push_back(nums[que.front()]);
for (int i = k; i < nums.size(); ++i) { // 枚举区间右端点
while(!que.empty() && nums[i] > nums[que.back()]) que.pop_back();
que.push_back(i);
while(que.front() <= i-k) {
que.pop_front();
}
res.push_back(nums[que.front()]);
}
return res;
}
};
这类区间最值问题还可以使用ST表或线段树来解决, 不过针对滑动窗口的区间最值问题, 还是单调队列更简便一些。
普通数组
53.最大子数组和
从前往后遍历, 用一个变量来记录和, 如果这个变量记录到的和小于0, 就将它重置为0; 因为它不会给答案带来正面的收益, 算上它之后数组的和只会更小。注意要处理全是负数的数组的情况, 此时答案就为数组中最大的负数。
56. 合并区间
刚开始打算使用使用一个大小为1e4的数组来标记区间, 但是发现这种方法不能处理[1, 4], [5, 7]的例子, 这个例子实际没有产生重叠, 但依旧会在数组中产生一个连续的不为0的区间。正确处理方式是对所有区间按照左端点进行排序, 然后就可以方便的进行合并操作了。
189.轮转数组
使用区间拷贝的库函数, 几行就搞定了。空间复杂度为O(1)的方法可以通过旋转数组来实现。
class Solution {
public:
void rotate(vector<int>& nums, int k) {
k %= nums.size();
vector<int> tmp(nums.rbegin(), nums.rbegin()+k);
copy(nums.begin(), nums.end()-k, nums.begin()+k);
copy(tmp.rbegin(), tmp.rend(), nums.begin());
}
};
238.除自身以外数组的乘积
预处理前缀乘积和后缀乘积即可, 其中一个预处理数组可以使用一个变量来简化, 另一个预处理数组可以使用返回结果数组来代替。
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
vector<int> res(nums.size());
res[0] = 1;
for (int i = 0; i < nums.size()-1; ++i) {
res[i+1] = res[i] * nums[i];
}
int t = 1;
for (int i = nums.size()-1; i >= 0; --i) {
res[i] *= t;
t *= nums[i];
}
return res;
}
};
矩阵
73.矩阵置零
直接说进阶方法,用第1行和第1列来记录第i行/第j列是否需要置零,第1行和第1列是否需要置0可以使用两个标志变量来记录。
54.螺旋矩阵
我采用了一种类似分治的想法,通过一个循环来不断输出数组,在循环的过程中,每输出一整行,剩下需要输出的矩阵的高就减1;同样每输出一整列,剩下需要输出的矩阵的宽就减1,直到剩余矩阵的宽或高变为0时,输出就结束了。通过一个变量来标记当前输出的方向。
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
int height = matrix.size();
int width = matrix[0].size();
pair<int, int> pos(0, 0);
/**
* 移动方向
* 1 --- 横向增大
* 2 --- 纵向增大
*
* -1 --- 横向减小
* -2 --- 纵向减小
*/
int dir = 1;
while(height && width) {
if (dir == 1) {
for (int i = 0; i < width; ++i) {
res.push_back(matrix[pos.first][pos.second+i]);
}
--height;
pos.second += width-1;
pos.first += 1;
dir = 2;
} else if (dir == 2) {
for (int i = 0; i < height; ++i) {
res.push_back(matrix[pos.first+i][pos.second]);
}
--width;
pos.first += height-1;
pos.second -= 1;
dir = -1;
} else if (dir == -1) {
for (int i = 0; i < width; ++i) {
res.push_back(matrix[pos.first][pos.second-i]);
}
--height;
pos.second -= width-1;
pos.first -= 1;
dir = -2;
} else if (dir == -2) {
for (int i = 0; i < height; ++i) {
res.push_back(matrix[pos.first-i][pos.second]);
}
--width;
pos.first -= height-1;
pos.second += 1;
dir = 1;
}
}
return res;
}
};
48.旋转图像
矩阵旋转90度,只需要沿对角线翻转矩阵,然后把矩阵逐行逆序即可。
240.搜索二维矩阵
遍历所有列, 二分查找。看了三叶的评论, 发现这个矩阵可以抽象成根节点在矩阵右上角的二叉搜索树, 太妙了。
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) { // 抽象成二叉搜索树
pair<int, int> pos{0, matrix[0].size()-1};
while(true) {
if (target > matrix[pos.first][pos.second]) { // 往右子树查找
if (pos.first == matrix.size()) return false;
++pos.first;
} else if (target < matrix[pos.first][pos.second]) {
if (pos.second == 0) return false;
--pos.second;
} else {
return true;
}
}
return false;
}
};
链表
160.相交链表
可以知道, 如果两个链表相交, 那么从链表的末尾到相交节点的距离一定是相等的, 我们在遍历两个链表的过程中, 可以先将指针移动到距离链表结尾距离相等的位置, 然后同时移动两个指针, 移动过程中查看两个指针是否指向了同一个节点。
206. 翻转链表
头插法即可。这里学习一下如何使用递归来完成翻转, 这里的递归和以前用到的递归形式不太一样, 不太好理解
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (!head || !head->next) return head;
ListNode* p = head;
ListNode* newHead = reverseList(head->next); // (1)假设head后的所有节点都完成了翻转
head->next->next = head; // (2)翻转后head的下一个节点变成了head前面紧邻的节点
head->next = nullptr; // (3)head->next置空
return newHead; // 返回翻转后的新头节点
}
};
我们现在取一个中间状态来讲解一下,假设现在递归调用到了处理节点2的情况,执行完(1)后链表的情况是这样的
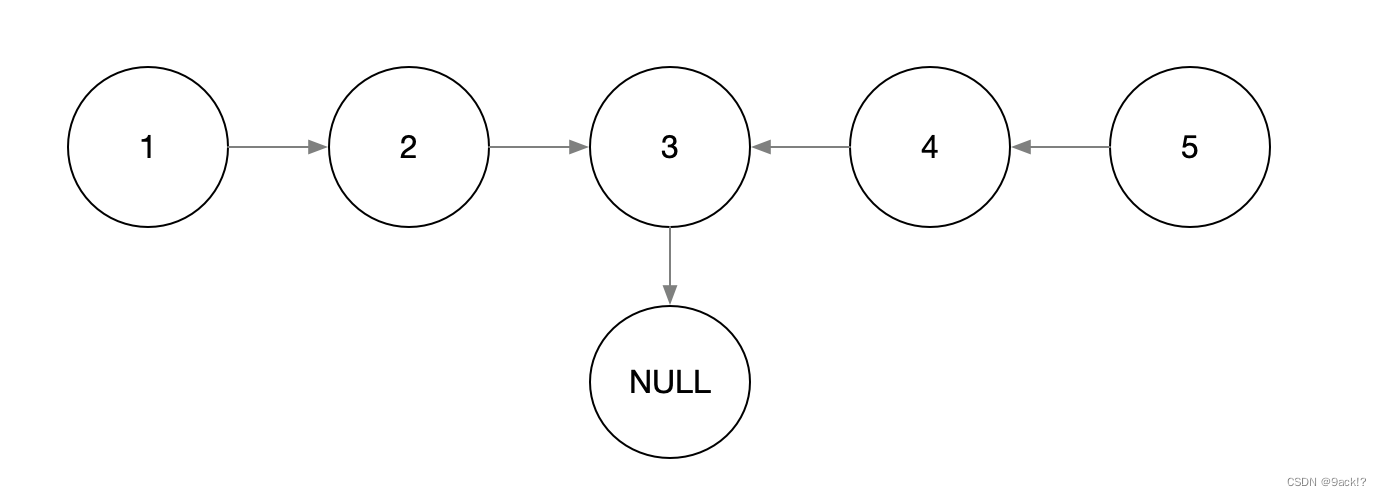
执行完(2)之后链表情况是这样的
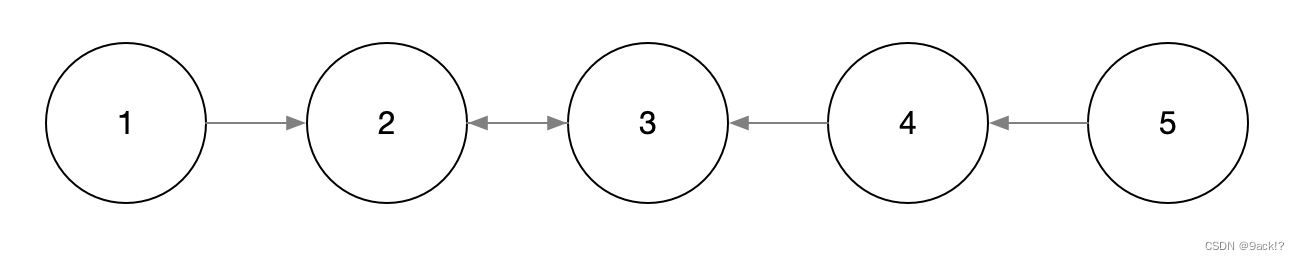
执行完(3)之后是这样的
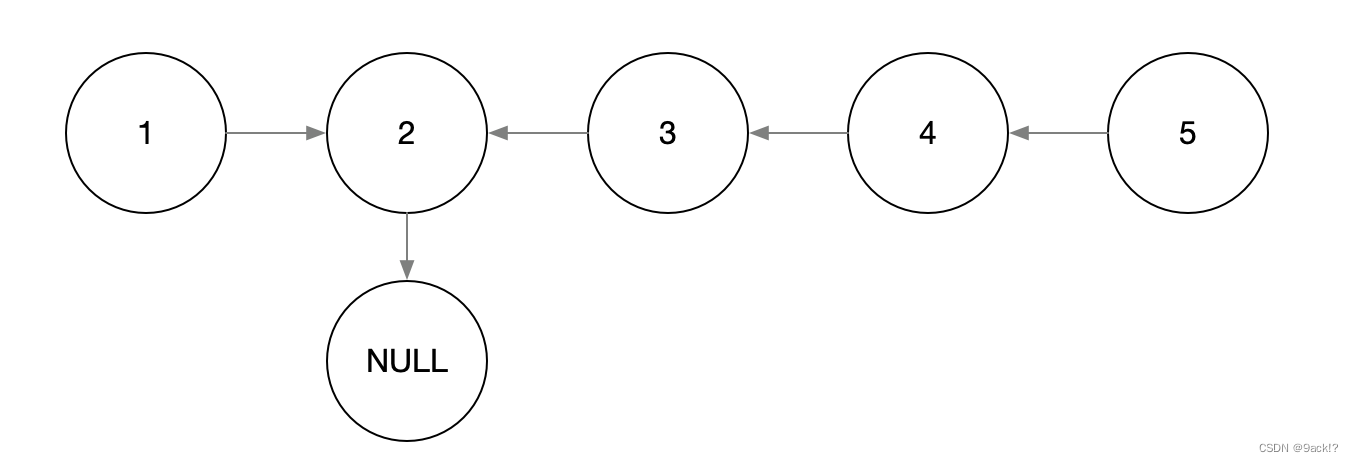
234.回文链表
判断回文串的方式就是找到中间节点, 使用两个指针分别向两边移动, 依次比较即可, 难点主要在链表不能简单的找到它的前驱节点, 我们可以利用递归函数的性质来比较
class Solution {
private:
ListNode* p;
int pos;
public:
bool isPalindrome(ListNode* head) {
ListNode* slow = head, *fast = head;
pos = 0;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
++pos;
}
if (fast) p = slow->next;
else p = slow;
return cmp(head, 0);
}
bool cmp(ListNode* head, int cnt) {
if (cnt < pos) {
if (cmp(head->next, cnt+1)) {
if (head->val == p->val) {
p = p->next;
return true;
} else {
return false;
}
} else {
return false;
}
}
return true;
}
};