【声明】本题目来源于卡码网(卡码网KamaCoder)
【提示:如果不想看文字介绍,可以直接跳转到C++编码部分】
【设计模式大纲】
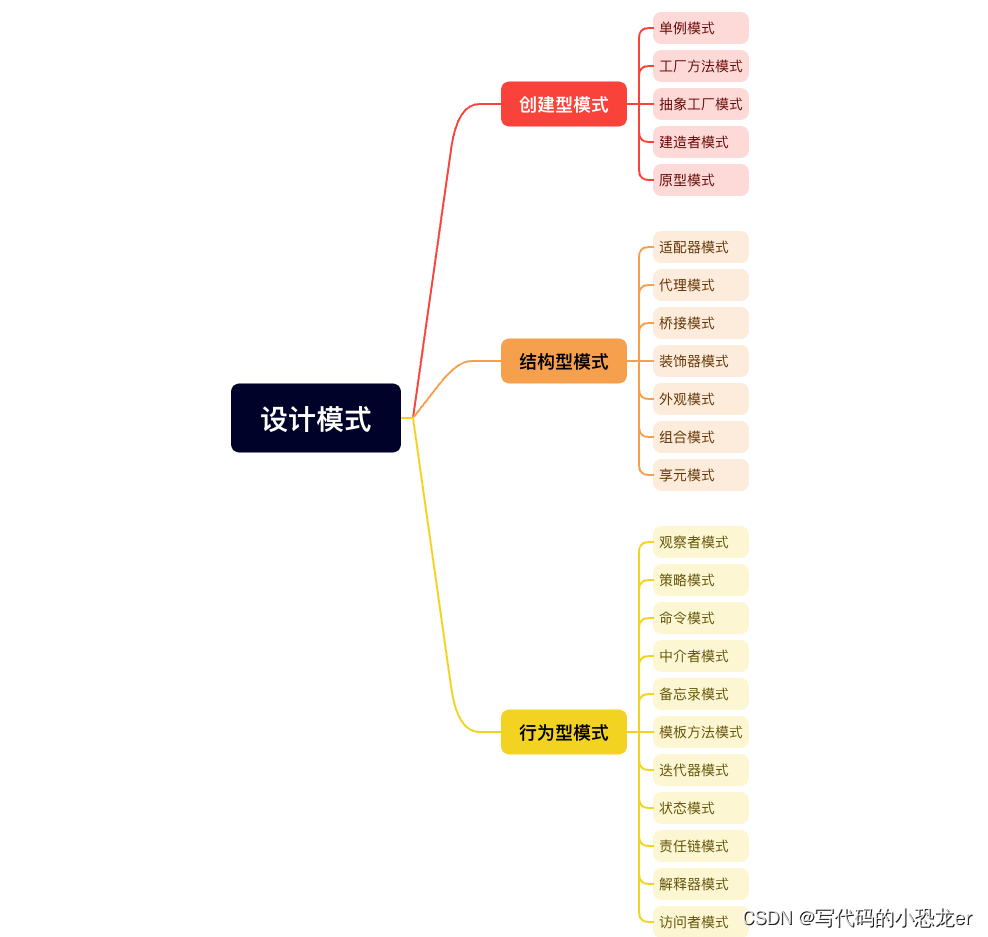
【简介】
--什么是解释器模式(第22种设计模式)
解释器模式(Interpreter Pattern)是⼀种行为型设计模式,它定义了⼀个语⾔的⽂法,并且建⽴⼀个【解释器】来解释该语⾔中的句子。
比如说SQL语法、正则表达式,这些内容比较简短,但是表达的内容可不仅仅是字⾯上的那些符号,计算机想要理解这些语法,就需要解释这个语法规则,因此解释器模式常⽤于实现编程语⾔解释器、正则表达式处理等场景。
【基本结构】
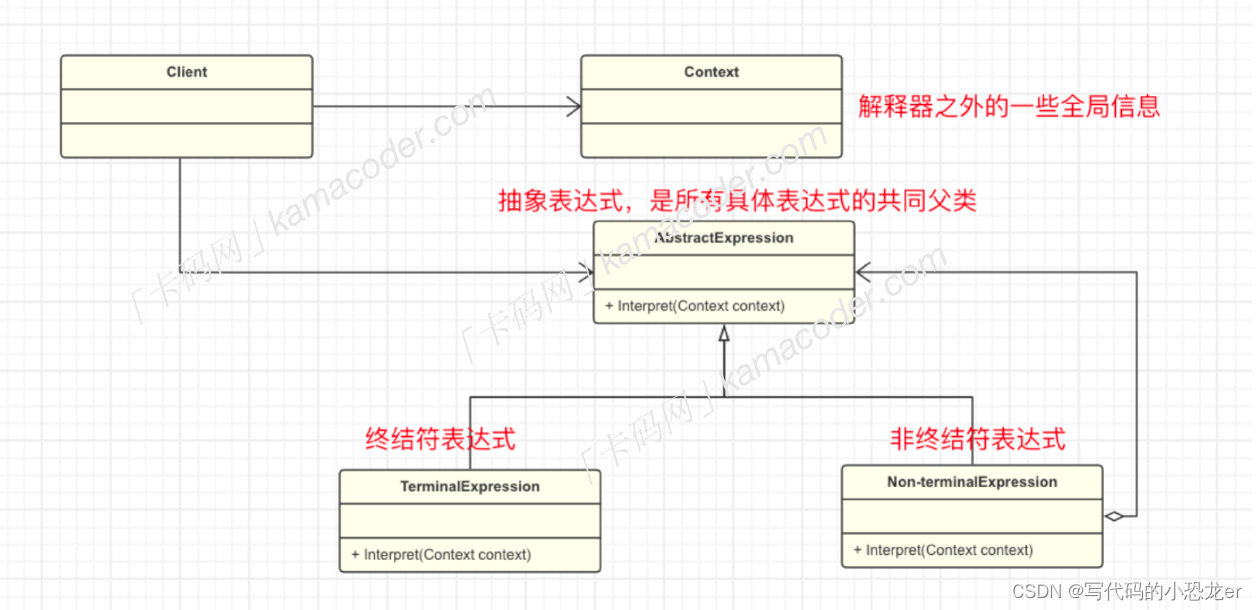
解释器模式主要包含以下⼏个角色:
- 1. 抽象表达式(Abstract Expression): 定义了解释器的接口,包含了解释器的⽅法 interpret 。
- 2. 终结符表达式(Terminal Expression): 在语法中不能再分解为更⼩单元的符号。
- 3. 非终结符表达式(Non-terminal Expression): 文法中的复杂表达式,它由终结符和其他⾮终结符组成。
- 4. 上下文(Context): 包含解释器之外的⼀些全局信息,可以存储解释器中间结果,也可以⽤于向解释器传递信息。
举例来说,表达式 "3 + 5 * 2",数字 "3" 和 "5", "2" 是终结符,⽽运算符 "+", "*"都需要两个操作数, 属于⾮终结符。
【简易实现-Java】
1. 创建抽象表达式接口:
定义解释器的接⼝,声明⼀个 interpret ⽅法,用于解释语⾔中的表达式。
// 抽象表达式接⼝
public interface Expression {
int interpret();
}2. 创建具体的表达式类:
实现抽象表达式接口,用于表示语⾔中的具体表达式。
public class TerminalExpression implements Expression {
private int value;
public TerminalExpression(int value) {
this.value = value;
}
@Override
public int interpret() {
return value;
}
}3. 非终结符表达式:
抽象表达式的⼀种,⽤于表示语⾔中的⾮终结符表达式,通常包含其他表达式。
public class AddExpression implements Expression {
private Expression left;
private Expression right;
public AddExpression(Expression left, Expression right) {
this.left = left;
this.right = right;
}
@Override
public int interpret() {
return left.interpret() + right.interpret();
}
}4. 上下文:
包含解释器需要的⼀些全局信息或状态。
public class Context {
// 可以在上下⽂中存储⼀些全局信息或状态
}5. 客户端:
构建并组合表达式,然后解释表达式。
public class Main {
public static void main(String[] args) {
Context context = new Context();
Expression expression = new AddExpression(
new TerminalExpression(1),
new TerminalExpression(2)
);
int result = expression.interpret();
System.out.println("Result: " + result);
}
}【使用场景】
当需要解释和执⾏特定领域或业务规则的语⾔时,可以使用解释器模式。例如,SQL解释器、正则表达式解释器等。但是需要注意的是解释器模式可能会导致类的层次结构较为复杂,同时也可能不够灵活,使用要慎重。
【C++编码部分】
1. 题目描述
小明正在设计一个计算器,用于解释用户输入的简单数学表达式,每个表达式都是由整数、加法操作符+、乘法操作符组成的,表达式中的元素之间用空格分隔,请你使用解释器模式帮他实现这个系统。
2. 输入描述
每行包含一个数学表达式,表达式中包含整数、加法操作符(+)和乘法操作符(*)。 表达式中的元素之间用空格分隔。
3. 输出描述
对于每个输入的数学表达式,每行输出一个整数,表示对应表达式的计算结果。
4. C++编码示例
注意: 其中的解析表达式函数比较抽象,但不是解释器模式的核心,无需太过关注,只需要了解到这种模式的特定即可。
/**
* @version Copyright (c) 2024 NCDC, Servo。 Unpublished - All rights reserved
* @file InterpreterMode.hpp
* @brief 解释器模式
* @autor 写代码的小恐龙er
* @date 2024/01/26
*/
#include <iostream>
#include <string>
#include <stack>
#include <vector>
using namespace std;
// 前置声明
// 表达式 接口类
class Expression;
// 终结符表达式类 -- 数字
class NumberExpression;
// 非终结符表达式 -- 加法运算符
class AddExpression;
// 非终结符表达式 -- 乘法运算符
class MultiplyExpression;
// 上下文类
class Context;
// 类的定义
// 表达式 接口类
class Expression
{
public:
virtual int Interpret() = 0;
virtual string ReturnType() = 0;
};
// 终结符表达式类 -- 数字
class NumberExpression : public Expression
{
private:
int _number;
public:
NumberExpression(int number){
this->_number = number;
}
// 重载接口函数
int Interpret() override{
return _number;
}
string ReturnType() override{
return "number";
}
};
// 非终结符表达式 -- 加法运算符
class AddExpression : public Expression
{
private:
Expression * _left;
Expression * _right;
public:
AddExpression(){}
AddExpression(Expression * left, Expression * right){
this->_left = left;
this->_right = right;
}
// 重载接口函数
int Interpret() override{
return _left->Interpret() + _right->Interpret();
}
string ReturnType() override{
return "+";
}
};
// 非终结符表达式 -- 乘法运算符
class MultiplyExpression : public Expression
{
private:
Expression * _left;
Expression * _right;
public:
MultiplyExpression(){}
MultiplyExpression(Expression * left, Expression * right){
this->_left = left;
this->_right = right;
}
// 重载接口函数
int Interpret() override{
return _left->Interpret() * _right->Interpret();
}
string ReturnType() override{
return "*";
}
};
// 上下文类
class Context
{
private:
stack<Expression *> _expressionSt;
public:
void PushExpression(Expression * expression){
_expressionSt.push(expression);
}
void PopExpression(){
_expressionSt.pop();
}
};
// 解析输入的表达式 【有点复杂 -- 花了一个多小时想出来的】
Expression *ParseExpression(string input){
// 存放 表达式类
vector<Expression *> result;
// 存放 加号表达式 【消除 乘号表达式】
stack<Expression *> resultAdd;
int i = 0;
// 本次时间复杂度为 O(n)的操作为 寻找出所有的 表达式类
while(i < (int)input.size()){
string number = "";
char temp = input[i];
while(temp >= '0' && temp <= '9'){
number += input[i++];
temp = input[i];
if(temp == ' ' || temp == '\0'){
result.push_back(new NumberExpression((int)atoi(number.c_str())));
}
}
if(temp == '+'){
result.push_back(new AddExpression());
}
else if(temp == '*'){
result.push_back(new MultiplyExpression());
}
i++;
}
// 由于 表达式 均是 数字 + 符号 的连接形式
// 则 我们可以 先将 所有的乘号 消除 转换为Multiplyexpression
// 最后将所有的 + 转换为-个AddExpression;
// 这个for 循环 找出所有乘号 时间复杂度 O(n)
int size = result.size();
for(i = 0; i < size; i++){
if(result[i] && result[i]->ReturnType() == "*"){
if(i - 1 >= 0 && i + 1 < size){
// 这行代码的目的是将 其中一个加数 pop出去 变成 乘数
if(!resultAdd.empty()) resultAdd.pop();
resultAdd.push(new MultiplyExpression(result[i - 1], result[i + 1]));
result[i] = nullptr;
i++;
result[i] = nullptr;
}
else return nullptr;
}
else if(result[i] && (result[i]->ReturnType() == "number" || result[i]->ReturnType() == "+")){
resultAdd.push(result[i]);
}
}
// 本次操作为 将所有的 加法 转换为 一个 表达式类
while(resultAdd.size() >= 3){
Expression *left = resultAdd.top();
resultAdd.pop();
Expression *add = resultAdd.top();
resultAdd.pop();
Expression *right = resultAdd.top();
resultAdd.pop();
// 将 加号 运算符 添加进 栈
add = new AddExpression(left, right);
resultAdd.push(add);
if(resultAdd.size() < 3) break;
}
return resultAdd.top();
}
// 在vs2022里面可以正常运行
// 测试用例:
// 2 + 3
// 2 * 3
// 2 + 2 * 3
// 2 * 3 + 2
// 2 + 2 * 3 + 1
// 2 * 3 + 1 + 3 * 2
int main()
{
// 新建上下文类
Context *context = new Context();
// 输入的表达式
string input = "";
while(std::cin >> input){
// 表达式解析
Expression *expression = ParseExpression(input);
if(expression){
// 通过上下文类来保存一些关键信息
context->PushExpression(expression);
// 通过一个 表达式 解析后的 唯一表达式来进行原酸
std::cout << expression->Interpret() << endl;
}
else std::cout << "Invalid expression." << endl;
}
delete context;
context = nullptr;
return 0;
}
......
To be continued.
【再有最后一种设计模式了! 下午更新】