这个专栏主要是用来分享一下我在 机器学习中的 学习笔记及一些 感悟,也希望对你的学习有帮助哦!感兴趣的小伙伴欢迎 私信或者 评论区留言!这一篇就更新一下《 白话机器学习中的数学——似然函数》!
- 什么是似然函数
似然函数 定义. 在 数理统计学 中, 似然函数是一种关于统计模型中的参数的函数 ,表示模型参数中的 似然性 。 似然函数在 推断统计学 (Statistical inference)中扮演重要角色,如在 最大似然估计 和费雪信息之中的应用等等。. "似然性"与"或然性"或" 概率 "意思相近,都是指某种事件发生的可能性,但是在 统计学 中,"似然性"和"或然性"或"概率"又有明确的区分。
- 案例分析
再上一篇文章中我们学习了逻辑回归,现在我们的任务就是来求参数的更新表达式,但是逻辑回归的目标函数与之前不一样,也就是和最小二乘法的不一样,一开始我们把 x 为横向的概率 P(y = 1|x) 定义为 fθ(x) 了。基于这一点,既然 fθ(x) 是 x 为横向时的概率……那么在 y = 1 时 fθ(x) = 1,y = 0 时 fθ(x) = 0 的关系就是理想的,我们把这句话换成这样的说法:
● y = 1 的时候,我们希望概率 P(y = 1|x) 是最大的
● y = 0 的时候,我们希望概率 P(y = 0|x) 是最大的
P(y = 1|x) 是图像为横向的概率,P(y = 0|x) 是图像为纵向的概率。这适用于全部的训练数据。对于一开始列举的那 6 个训练数据,我们期待的最大概率是这样的:

而且,假定所有的训练数据都是互不影响、独立发生的,这种情况下整体的概率就可以用下面的联合概率来表示。

第 1 次的概率是 P(y(1) = 0|x(1)),第 2 次的概率是P(y(2) = 0|x(2))……我们要计算的是连续发生 6 次的概率,而且联合概率的表达式是可以一般化的,写法如下:
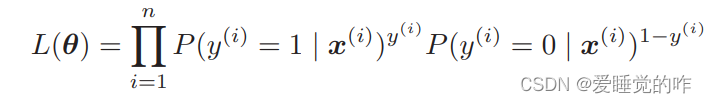
我们分别考虑 y(i) 为 1 或为 0 时的 P(y(i) = 1|x(i))y(i)P(y(i) = 0|x(i)1−y(i)。P 右上角的 y(i) 和 1 − y(i) 表示指数,首先向指数 y(i) 代入 1。

这样就只剩 y(i) = 1 的概率了。y(i) = 0 的时候也一样

这个表达式利用了任何数字的 0 次方都是 1 的特性。比起区分各种情况的写法,还是汇总到一个表达式的写法更简单。接下来考虑一下使这个目标函数最大化的参数 θ 吧。
回归的时候处理的是误差,所以要最小化,而现在考虑的是联合概率,我们希望概率尽可能大,所以要最大化。这里的目标函数 L(θ) 也被称为似然,函数的名字 L 取自似然的英文单词 Likelihood 的首字母。它的意思是最近似的。
我们可以认为似然函数 L(θ) 中,使其值最大的参数 θ 能够最近似地说明训练数据。似然是不容易理解的概念,这里不懂它也没关系。只要记住这个词就行了。