190. Reverse Bits（颠倒二进制位）

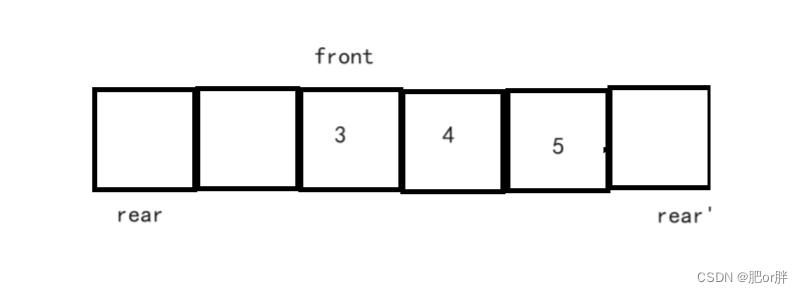
题目要求我们将一个数的二进制位进行颠倒，画出图示如下(以8位二进制为例)：

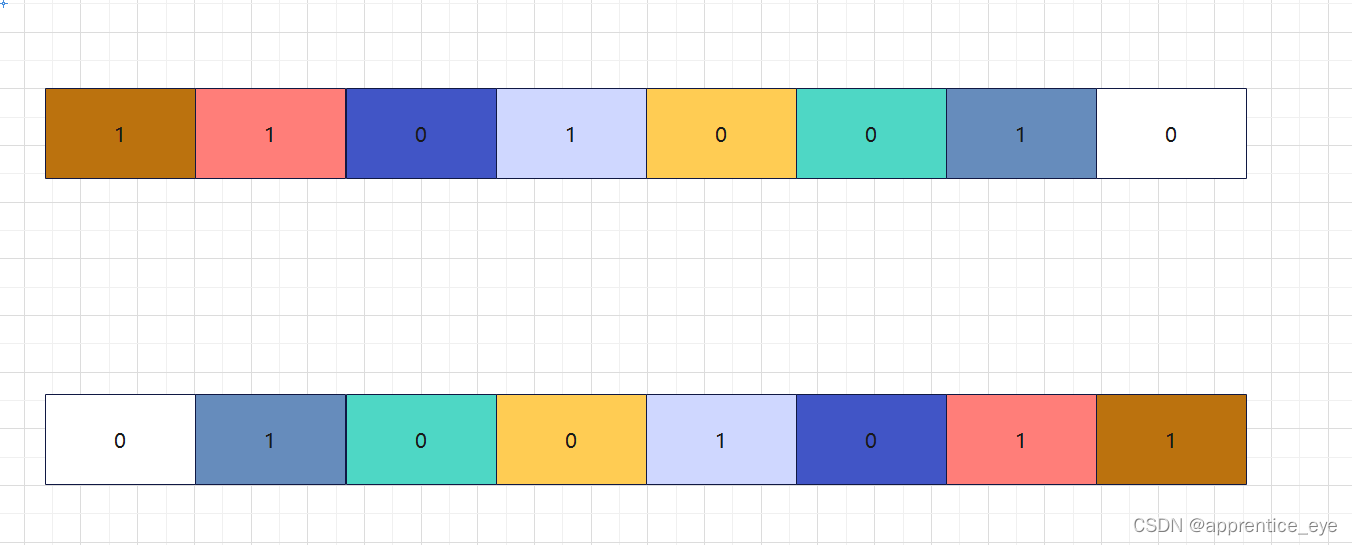
显然对于这种问题我们需要用到位操作，我们需要将原数的每一位取出来然后颠倒之后放进另一个数。
我们需要先知道离散数学中的几个公式$$\begin{gathered} p\vee 1=1 \\ p\vee 0=p \\ p\wedge 1=p \\ p\wedge 0=0 \end{gathered}$$
知道上述的公式之后我们就可以对数进行取出位数。
如下图所示

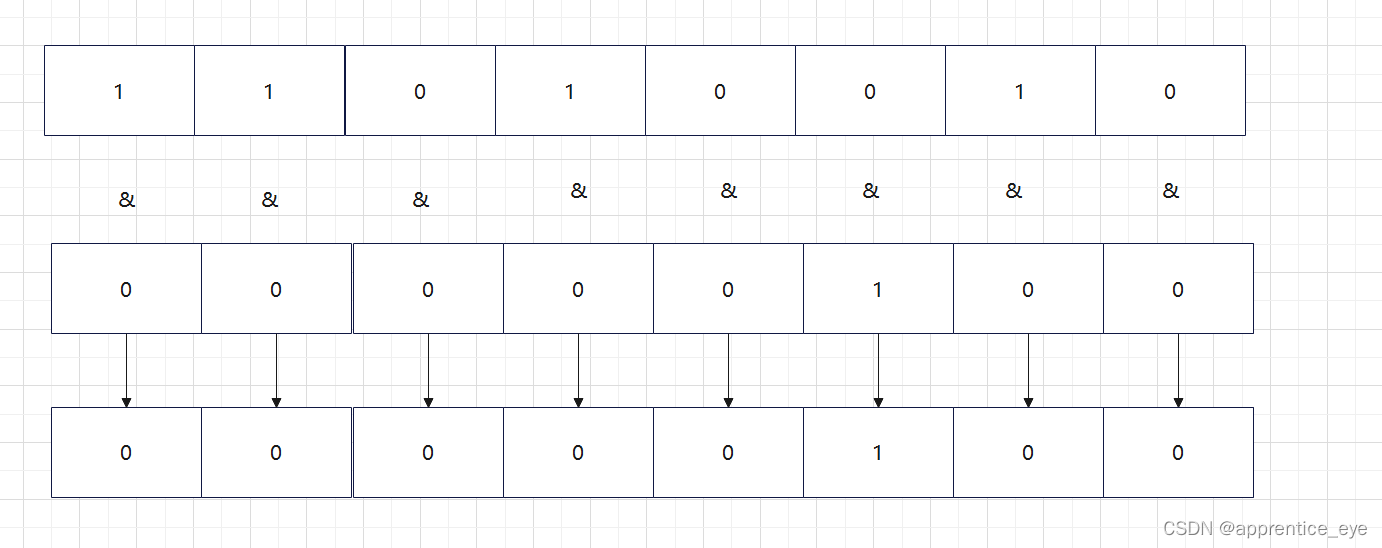
也就是说我们要取出哪一位就让哪一位&上1就行了。
但是如何控制对应位为1而其他位为0呢？我们知道c语言中移位操作>>与<<,分别代表左移与右移，让对应位为1我们只需要让1进行<<操作就行。
经过移位与&操作我们可以得到一个除了要取出位为原二进制数中对应位之外，其余位全为0的数。
现在取出哪一位的问题已经解决了，我们知道$p\vee 0==p$也就是说我们要保证接收对应位的数的对应位等于0，其余的均不许要进行改变，因为我们取出数的位除了取出的那一位其余位全为0，并不会改变我们的接收数。由此我们有了以下的思路。
因为有符号整型的数在进行移位操作的时候并不能操作符号位所以我们需要先进行符号位的改变。或者使用无符号整型。

uint32_t reverseBits(uint32_t n) {
    int x = 0;
    if(n%2==0){
        x = 0;
    }else{
        x = INT_MIN;
    }
    for(int i =0; i<31; i++){
        n = n>>1;
        x |= ((n&1)<<(30-i));
    }
    return x;
}

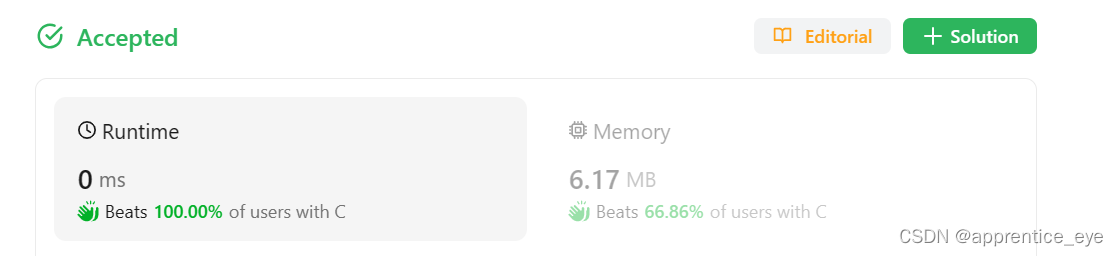
运行结果截图:

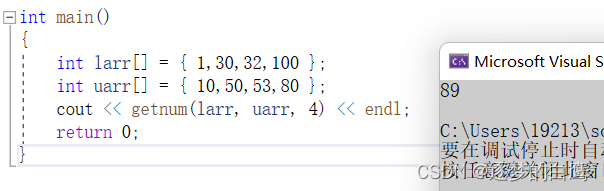
191. Number of 1 Bits( 位1的个数)

经过上面这一题之后我们已经知道怎么取出对应位了，取出对应位之后判断是否为1就行了。

int hammingWeight(uint32_t n) {
    int count = 0;
    while(n){
        if(n&1){
            count++;  
        }
        n=n>>1;
    }
    return count;
}

运行结果截图: