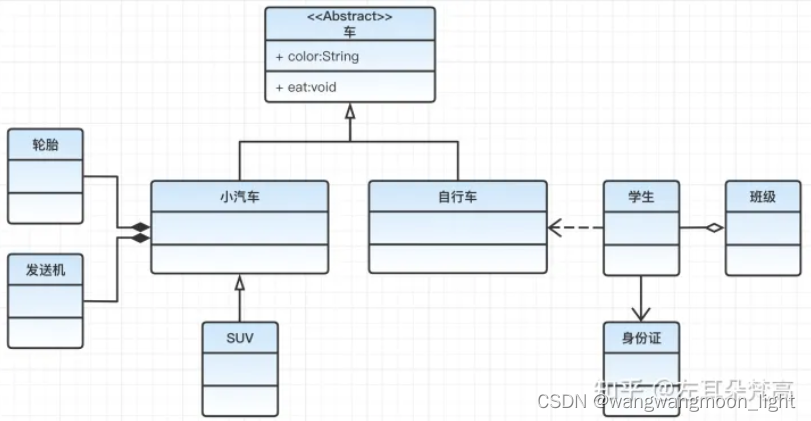
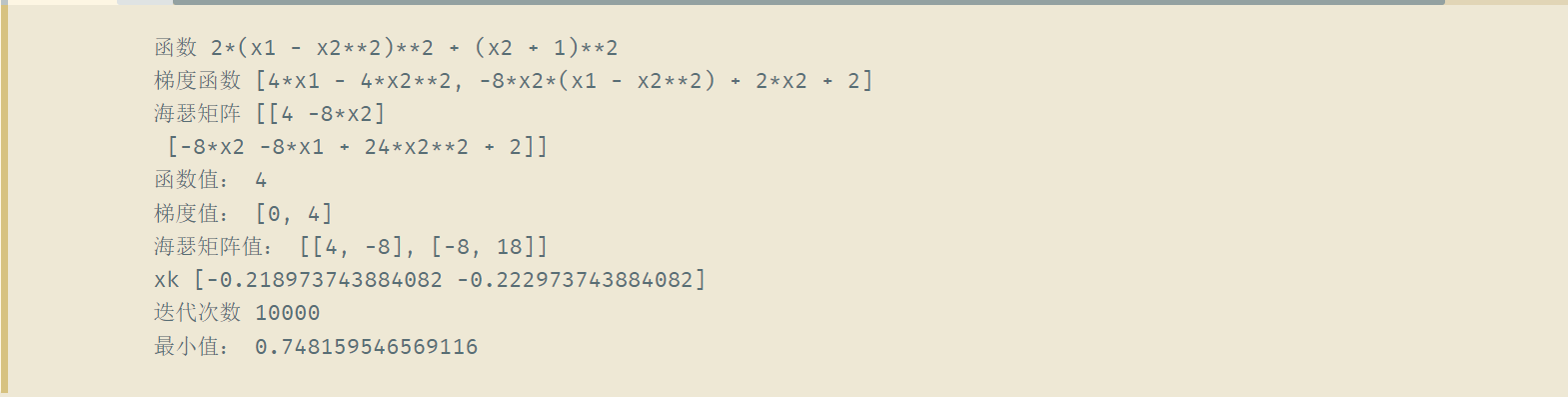
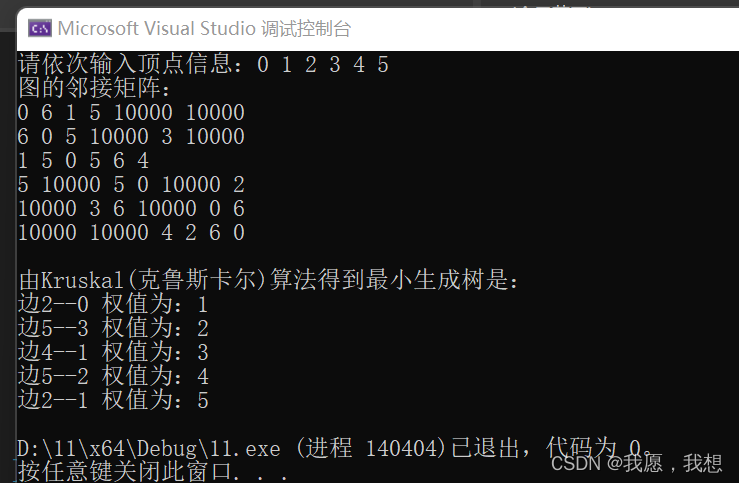
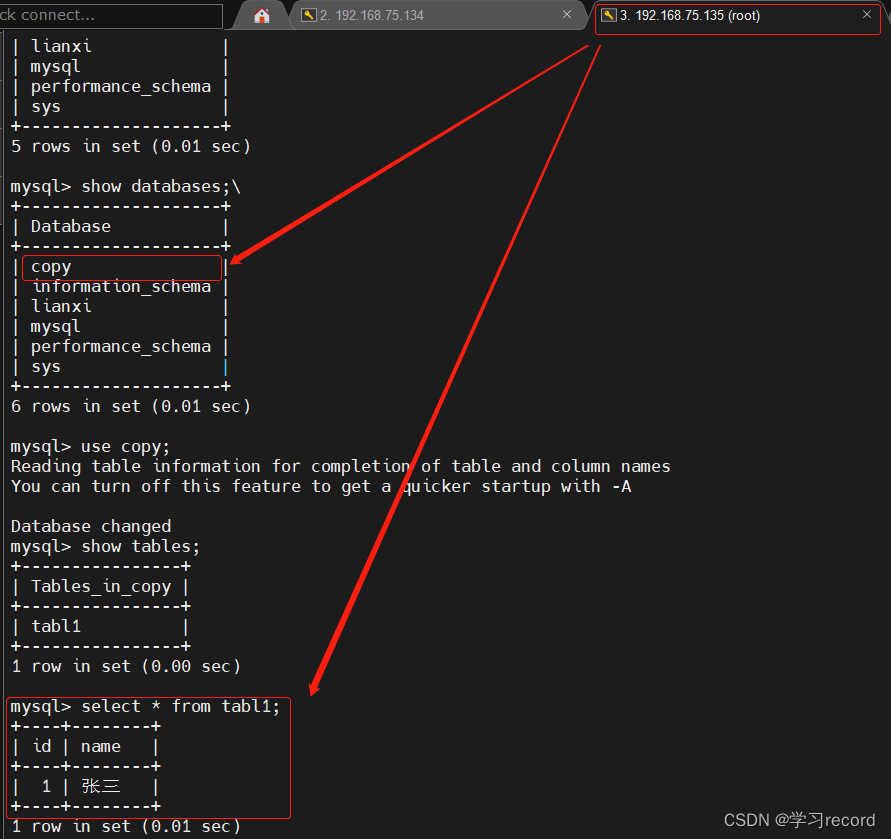
题目展示

 题目要点

题目其实本身的思路非常简单，就是把两个数组给合并起来，然后寻找中位数，具体可以参考我们使用归并排序时候的最后一步，这题的难点其实在于（1）时间压缩到logn+m（2）边界情况

难点处理

（1）复杂度问题确实不太好搞

（2）边界情况需要更多的注意

（1）情况1：在输入的时候有一个向量是空的

（2）情况2：在进行比较，寻找数字的时候，可能会让某一个向量走到了尽头’

（3）情况3：要记得判断一下总长度是奇数还是偶数

这里有一个错误地点就是：直接寻找中位数的时候，注意一下第mid个元素在mid-1的位置上

坑死了真的是

处理思路

（1）首先先判断，是否有哪个队列是空的，因为题目的限制是没有队列为空，所以只要判断其中一个为空就可以。然后判断一下另一个队列里面的长度是奇数还是偶数，再去寻找可用的数字输出

（2）如果两个队列都不是空的，就计算一下这俩的总长度，寻找中位数所在的位置

这里我们假设有一个变量是mid=（length）/2;

如果总长度为奇数，我们就要输出第mid+1个数字

如果总长度为偶数，我们就要输出mid和mid+1个数字的平均数

然后for循环mid+1次即(这里把mid个数字和mid+1个数字都得出来，再根据具体情况进行计算)

（3）在每次for循环中，首先判断是不是某个向量已经为空了

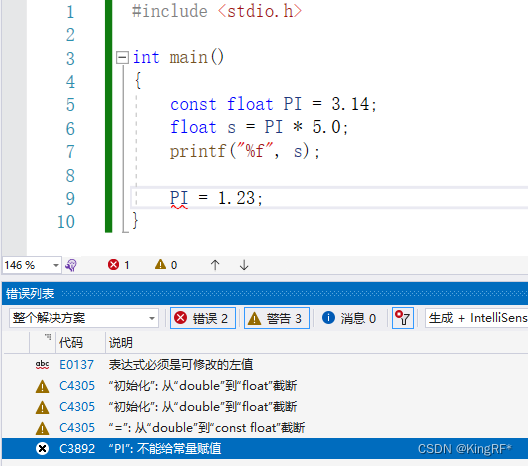
具体代码如下，不过成绩不是很乐观

double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
     int n=nums1.size();
     int m=nums2.size();
     int mid=(m+n)/2;
     double temp[2];
     int point=0;
     //这题整体的思路就有问题
     if(n==0){//第一种情况，如果nums1为空队列
         if(m%2==0){
             return (nums2[mid-1]+nums2[mid+1-1])/2.0;
         }else{
             return nums2[mid+1-1];
         }
     }else if(m==0){//第二种情况，如果nums2为空队列
         if(n%2==0){
             return (nums1[mid-1]+nums1[mid+1-1])/2.0;
         }else{
             return nums1[mid+1-1];
         }
     }else{//这俩目前都不是空队列
         for(int i=1;i<=mid+1;i++){
             if(!nums1.empty()&&!nums2.empty()){//如果这俩目前都不是空的
                 if(nums1.front()>nums2.front()){
                     if(i>=mid){
                         temp[point++]+=nums2.front();
                     }
                     nums2.erase(nums2.begin());
                 }else{
                     if(i>=mid){
                         temp[point++]+=nums1.front();
                     }
                     nums1.erase(nums1.begin());
                 }
             }else if(nums1.empty()){//如果第一个队列空了
                 if(i>=mid){
                     temp[point++]+=nums2.front();
                 }
                 nums2.erase(nums2.begin());
             }else{//如果第二个队列空了
                 if(i>=mid){
                     temp[point++]+=nums1.front();
                 }
                 nums1.erase(nums1.begin());
             }
         }
        return (m+n)%2==0?(temp[0]+temp[1])/2.0:temp[1];
     }


}