6-1P：推导RNN反向传播算法BPTT.

6-2P：设计简单RNN模型，分别用Numpy、Pytorch实现反向传播算子，并代入数值测试.、

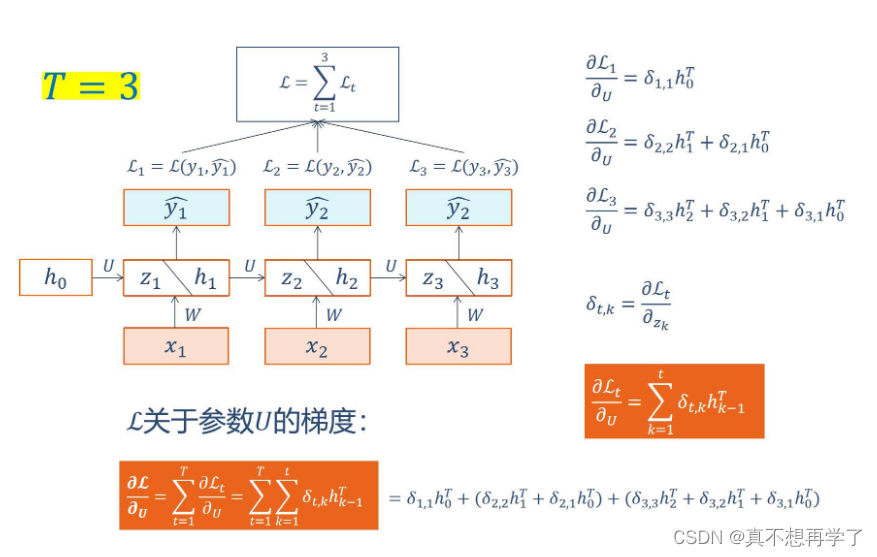
forward：

我们知道循环卷积网络的cell的计算公式为：
$${\mathrm{s}}_t=f(U{\mathrm{x}}_t+W{\mathrm{s}}_{t-1})$$
展开为：
$$\left[\begin{array}{c}{s}_1^t\\ s_2^t\\ .\\ .\\ s_n^t\end{array}\right]=f(\left[\begin{array}{c}{u}_{11}{u}_{12}...u_{1m}\\ u_{21}{u}_{22}...u_{2m}\\ .\\ .\\ u_{n1}{u}_{n2}...u_{nm}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ .\\ .\\ x_m\end{array}\right]+\left[\begin{array}{c}{w}_{11}{w}_{12}...w_{1n}\\ w_{21}{w}_{22}...w_{2n}\\ .\\ .\\ w_{n1}{w}_{n2}...w_{nn}\end{array}\right]\left[\begin{array}{c}{s}_1^{t-1}\\ s_2^{t-1}\\ .\\ .\\ s_n^{t-1}\end{array}\right])$$
这里的矩阵运算将输入x和s规范到了相同的尺寸（n，1）。

BPTT：

由于循环神经网络的特殊性，它和全连接神经网络十分相似，因此可以有一个参照。
BPTT算法是针对循环层的训练算法，它的基本原理和BP算法是一样的，大致包含四个步骤：
1.前向计算每个神经元的输出值；
这个就是前面的forward部分。
2.反向计算误差函数E对当前神经元i的加权输入的偏导数；

这个加权输入实际上是指：
$${\mathrm{net}}_t=U{\mathrm{x}}_t+W{\mathrm{s}}_{t-1}$$
接下来推导：
$$\frac{\partial {\mathrm{net}}_t}{\partial {\mathrm{net}}_{t-1}}=\frac{\partial {\mathrm{net}}_t}{\partial {\mathrm{s}}_{t-1}}\frac{\partial {\mathrm{s}}_{t-1}}{\partial {\mathrm{net}}_{t-1}}$$
前一项：

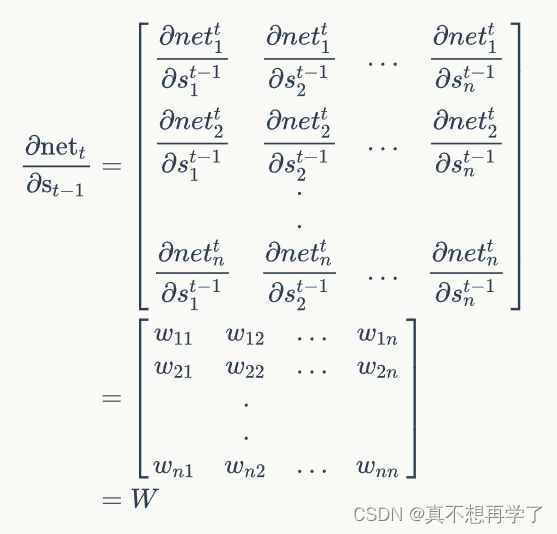
后一项：

因此：

这就是误差项对上一个神经元输入的偏导数每一步链式求导的计算方法，将当前时刻的误差项展开，每多一个时刻就会多一步链式求导，也就是上面这个计算过程，这个部分对应全连接BP的最外层偏导。
同样的还有对当前输入的偏导计算，这个就简单一些了，因为不涉及上个神经元的输入。
同样，表示上一个神经元的

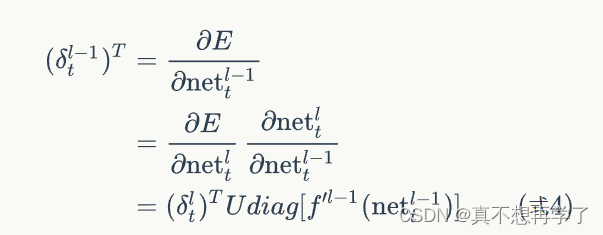
3.计算每个权重的梯度。
首先，我们计算误差函数E对权重矩阵W的梯度。
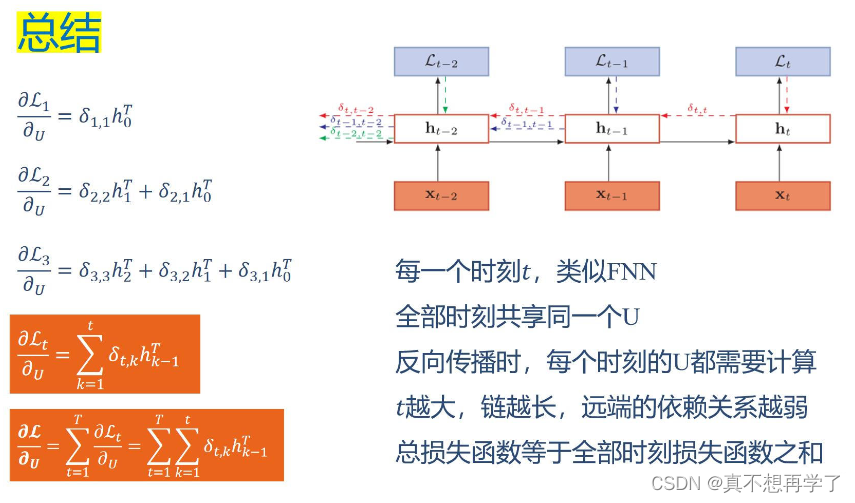
上图展示了我们到目前为止，在前两步中已经计算得到的量，包括每个时刻t 循环层的输出值，以及误差项。

同权重矩阵W类似，我们可以得到权重矩阵U的计算方法。

和权重矩阵W一样，最终的梯度也是各个时刻的梯度之和：

4.用SGD算法更新权重。
这一步就非常简单了，就是使用随机梯度下降算法实现参数更新，梯度有了，只需要引入学习率lr就够了。

全部代码；

import numpy as np

class RecurrentLayer():
    def __init__(self, input_width, state_width,
                 activator, learning_rate):
        self.input_width = input_width
        self.state_width = state_width
        self.activator = activator
        self.learning_rate = learning_rate
        self.times = 0       # 当前时刻初始化为t0
        self.state_list = [] # 保存各个时刻的state
        self.state_list.append(np.zeros(
            (state_width, 1)))           # 初始化s0
        self.U = np.random.uniform(-1e-4, 1e-4,
            (state_width, input_width))  # 初始化U
        self.W = np.random.uniform(-1e-4, 1e-4,
            (state_width, state_width))  # 初始化W

    def forward(self, input_array):
        '''
        根据『式2』进行前向计算
        '''
        self.times += 1
        state = (np.dot(self.U, input_array) +
                 np.dot(self.W, self.state_list[-1]))
        element_wise_op(state, self.activator.forward)
        self.state_list.append(state)

    def backward(self, sensitivity_array, 
                 activator):
        '''
        实现BPTT算法
        '''
        self.calc_delta(sensitivity_array, activator)
        self.calc_gradient()

    def update(self):
        '''
        按照梯度下降，更新权重
        '''
        self.W -= self.learning_rate * self.gradient

    def calc_delta(self, sensitivity_array, activator):
        self.delta_list = []  # 用来保存各个时刻的误差项
        for i in range(self.times):
            self.delta_list.append(np.zeros(
                (self.state_width, 1)))
        self.delta_list.append(sensitivity_array)
        # 迭代计算每个时刻的误差项
        for k in range(self.times - 1, 0, -1):
            self.calc_delta_k(k, activator)

    def calc_delta_k(self, k, activator):
        '''
        根据k+1时刻的delta计算k时刻的delta
        '''
        state = self.state_list[k+1].copy()
        element_wise_op(self.state_list[k+1],
                    activator.backward)
        self.delta_list[k] = np.dot(
            np.dot(self.delta_list[k+1].T, self.W),
            np.diag(state[:,0])).T

    def calc_gradient(self):
        self.gradient_list = [] # 保存各个时刻的权重梯度
        for t in range(self.times + 1):
            self.gradient_list.append(np.zeros(
                (self.state_width, self.state_width)))
        for t in range(self.times, 0, -1):
            self.calc_gradient_t(t)
        # 实际的梯度是各个时刻梯度之和
        self.gradient = reduce(
            lambda a, b: a + b, self.gradient_list,
            self.gradient_list[0]) # [0]被初始化为0且没有被修改过

    def calc_gradient_t(self, t):
        '''
        计算每个时刻t权重的梯度
        '''
        gradient = np.dot(self.delta_list[t],
            self.state_list[t-1].T)
        self.gradient_list[t] = gradient

    def reset_state(self):
        self.times = 0       # 当前时刻初始化为t0
        self.state_list = [] # 保存各个时刻的state
        self.state_list.append(np.zeros(
            (self.state_width, 1)))      # 初始化s0


def data_set():
    x = [np.array([[1], [2], [3]]),
         np.array([[2], [3], [4]])]
    d = np.array([[1], [2]])
    return x, d


def gradient_check():
    '''
    梯度检查
    '''
    # 设计一个误差函数，取所有节点输出项之和
    error_function = lambda o: o.sum()
    
    rl = RecurrentLayer(3, 2, IdentityActivator(), 1e-3)

    # 计算forward值
    x, d = data_set()
    rl.forward(x[0])
    rl.forward(x[1])
    
    # 求取sensitivity map
    sensitivity_array = np.ones(rl.state_list[-1].shape,
                                dtype=np.float64)
    # 计算梯度
    rl.backward(sensitivity_array, IdentityActivator())
    
    # 检查梯度
    epsilon = 10e-4
    for i in range(rl.W.shape[0]):
        for j in range(rl.W.shape[1]):
            rl.W[i,j] += epsilon
            rl.reset_state()
            rl.forward(x[0])
            rl.forward(x[1])
            err1 = error_function(rl.state_list[-1])
            rl.W[i,j] -= 2*epsilon
            rl.reset_state()
            rl.forward(x[0])
            rl.forward(x[1])
            err2 = error_function(rl.state_list[-1])
            expect_grad = (err1 - err2) / (2 * epsilon)
            rl.W[i,j] += epsilon
            print 'weights(%d,%d): expected - actural %f - %f' % (
                i, j, expect_grad, rl.gradient[i,j])


def test():
    l = RecurrentLayer(3, 2, ReluActivator(), 1e-3)
    x, d = data_set()
    l.forward(x[0])
    l.forward(x[1])
    l.backward(d, ReluActivator())
    return 

总结：RNN的参数更新和全连接的BP算法还是有很大差别的，这也是为什么把RNN单独形成了一个板块，虽然有部分功能的计算很相似，但是也只是部分而已，他们都有各自的特点。
附：这两天也中招了，很难受，希望老师同学们都能保护好自己，当然，也中招了的话就注意休息，多喝热水。。。
ref：
https://blog.csdn.net/segegse/article/details/127708468
https://zybuluo.com/hanbingtao/note/541458