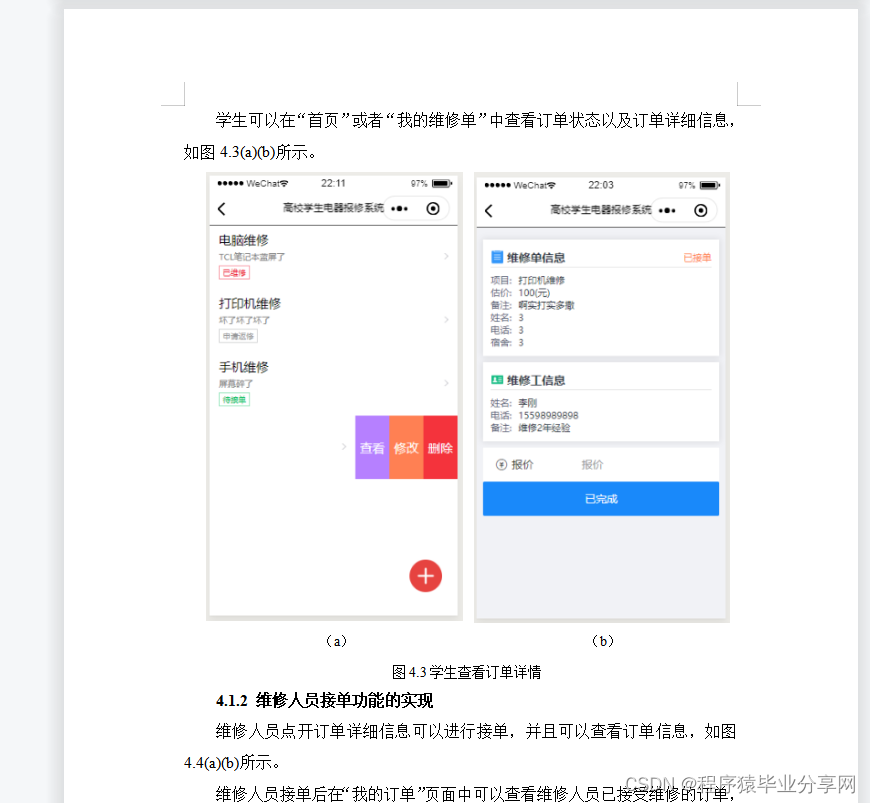
文章目录

一：次梯度算法
- （1）次梯度算法结构
- （2）应用举例-LASSO问题求解
二：牛顿法
- （1）经典牛顿法
- （2）修正牛顿法
三：拟牛顿法
- （1）拟牛顿条件
- （2）DFP算法

一：次梯度算法

对于梯度下降法，其前提是目标函数 $f (x)$ 是一阶可微的，但是在实际应用中经常会遇到不可微的函数，对于这类函数我们无法在每个点处求出梯度，但往往它们的最优值都是在不可微点处取到的，所以为了能够处理这种情形，本节介绍次梯度算法

（1）次梯度算法结构

假设 $f (x)$ 为凸函数，但不一定可微，考虑如下问题

$\mathop{min}\limits_{x} f(x)$

一阶充要条件： $x^{*}$ 是一个全局极小点<=> $0\in \partial f(x^{*})$
因此可以通过计算凸函数的次梯度集合中包含 $0$ 的点来求解其对应的全局极小点

为了极小化一个不可微的凸函数 $f$ ，可类似梯度法构造如下次梯度算法的迭代格式

$x^{k+1}=x^{k}-\alpha_{k}g^{k}, \quad g^{k}\in \partial f(x^{k})$

其中 $\alpha_{k}>0$ ，通常有如下4种选择方式

固定步长 $\alpha_{k}=\alpha$
固定 $x^{k+1}-x^{k}||$ ，即 $\alpha_{k}||g^{k}||$ 为常数
消失步长 $\alpha_{k} \rightarrow 0$ ，且 $\sum\limits_{k=0}^{\infty}a_{k}=+\infty$
选取 $\alpha_{k}$ 使其满足某种线搜索准则

（2）应用举例-LASSO问题求解

考虑LASSO问题：

$\quad f(x)=\frac{1}{2}||Ax-b||^{2}+u||x||_{1}$

容易得知 $f (x)$ 的一个次梯度为

$g=A^{T}(Ax-b)+usign(x)$

$s i g n (x)$ 是关于 $x$ 逐分量的符号函数

因此，LASSO问题的次梯度算法为

$x^{k+1}=x^{k}-\alpha_{k}(A^{T}(Ax^{k}-b)+usign(x^{k}))$

步长 $a_{k}$ 可选为固定步长或消失步长

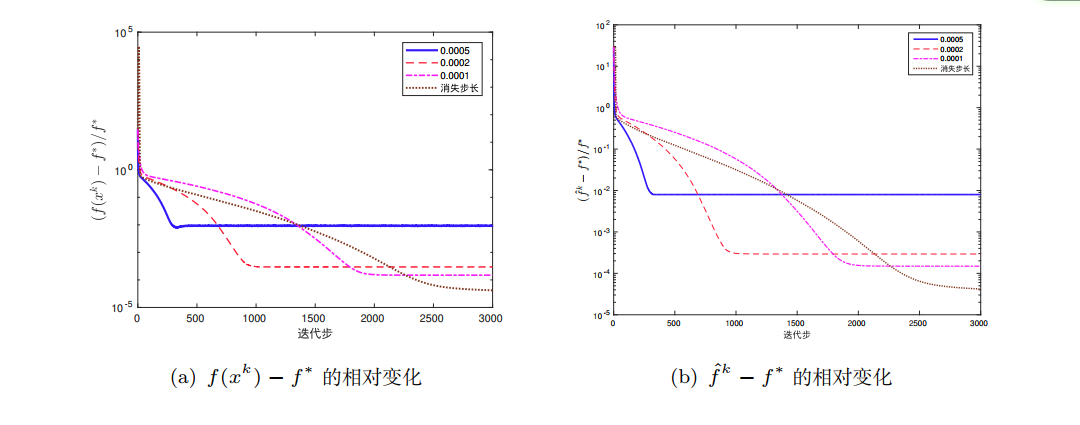
如下，正则化参数 $u = 1$ ，分别选取固定步长 $a_{k}=0.0005$ , $a_{k}=0.0002$ , $a_{k}=0.0001$ 以及消失步长 $a_{k}=\frac{0.002}{\sqrt{k}}$ 。可以发现，在3000步以内，使用不同的固定步长最终会到达次优解，函数值下降到一定程度便稳定在某个值附近；而使用消失步长算法最终将会收敛；另外次梯度算法本身是非单调方法，因此在求解过程中需要记录历史中最好的一次迭代来作为算法的最终输出

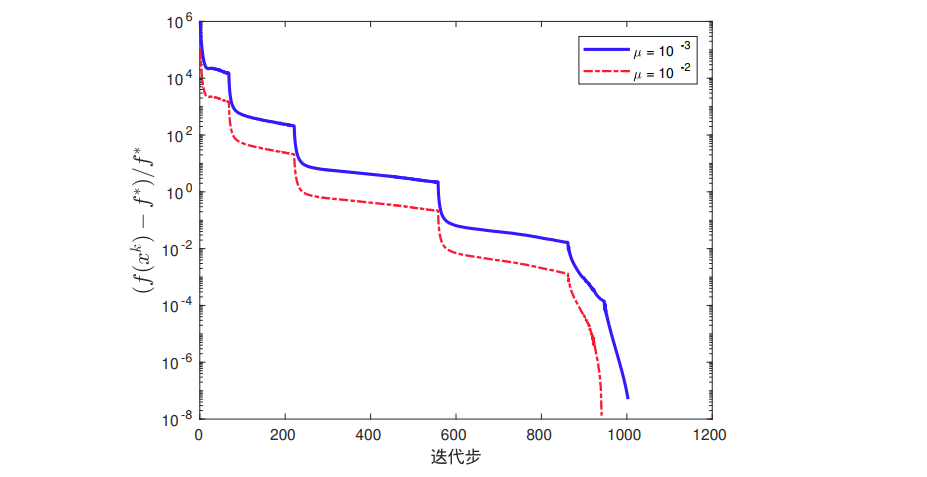
在这里插入图片描述

对于 $u=10^{-2},10^{-3}$ ，我们采用连续化次梯度算法进行求解

在这里插入图片描述

二：牛顿法

使用梯度下降法，我们给出的迭代格式为

$x^{k+1}=x^{k}-\alpha_{k}\nabla f(x^{k})$

由于梯度下降的基本策略是沿一阶最速下降方向迭代。当 $\nabla^{2}f(x)$ 的条件数较大时，它的收敛速度比较缓慢（只用到了一阶信息）。因此如果 $f (x)$ 足够光滑，我们可以利用 $f (x)$ 的二阶信息改进下降方向，以加速算法的迭代

（1）经典牛顿法

经典牛顿法：对于可微二次函数 $f (x)$ ，对于第 $k$ 步迭代，我们考虑目标函数 $f$ 在点 $x_{k}$ 的二阶泰勒近似

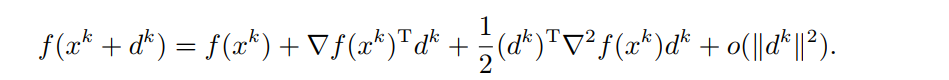
在这里插入图片描述

忽略高阶项 $o(||d^{k}||^{2})$ ，并将等式右边视作 $d^{k}$ 的函数并极小化，则
$\nabla^{2}f(x^{k})d^{k}=-\nabla f(x^{k})$

上式称其为牛顿方程， $d^{k}$ 叫做牛顿方向

若 $\nabla^{2}f(x^{k})$ 非奇异，则可得到迭代格式

$x^{k+1}=x^{k}-\nabla^{2}f(x^{k})^{-1}\nabla f(x^{k})$

注意：步长 $\alpha_{k}=1$

此迭代格式称之为经典牛顿法

经典牛顿法收敛速度很快，但是在使用中会有一些限制因素

初始点 $x^{0}$ 需要距离最优解充分近（也即牛顿法只有局部收敛性）。当 $x^{0}$ 距离最优解较远时，牛顿法在多数情况下会失效
海瑟矩阵 $\nabla^{2}f(x^{*})$ 需正定，半正定条件下可能退化到 $Q$ -线性收敛
$\nabla^{2}f(x^{*})$ 的条件系数较高时，将对初值的选择作出较为严格的要求
海瑟矩阵 $\nabla^{2}f(x^{*})$ 需要为正定矩阵。应用时常常以梯度类算法先求得较低精度的解，然后用牛顿法加速

在这里插入图片描述

（2）修正牛顿法

在实际应用中 $x^{k+1}=x^{k}-\nabla^{2}f(x^{k})^{-1}\nabla f(x^{k})$ 几乎是不能使用的，这是因为

每一步迭代需要求解一个 $n$ 维线性方程组，这导致在高维问题中计算量很大，而且海瑟矩阵又不容易存储
当海瑟矩阵不正定时，又牛顿方程给出的解 $d^{k}$ 的性质较差
当迭代点距最优值较远时，直接选取步长 $a_{k}=1$ 会使迭代极其不稳定，在有些情况下迭代点会发散

修正牛顿法：为了克服上述缺陷，我们对经典牛顿法做出某种修正或者变形，提出了修正牛顿法，使其成为真正可以使用的算法。这里介绍带线搜索的修正牛顿法，其基本思想是对牛顿方程中的海瑟矩阵 $\nabla^{2}f(x^{k})$ 进行修正，使其变为正定矩阵，同时引入线搜索以改善算法稳定性，其算法框架如下

在这里插入图片描述
上述算法中， $B^{k}$ （即 $E^{k}$ ）的选取较为关键，需要注意

$B^{k}$ 应该具有较低的条件数
对 $\nabla^{2}f(x)$ 的改动较小，以保存二阶信息
$B^{k}$ 本身的计算代价不应该太高

在这里插入图片描述

import numpy as np
from sympy import *

# 计算梯度函数
def cal_grad_funciton(function):
    res = []
    x = []
    x.append(Symbol('x1'))
    x.append(Symbol('x2'))
    for i in range(len(x)):
        res.append(diff(function, x[i]))
    return res

# 定义目标函数
def function_define():
    x = []
    x.append(Symbol('x1'))
    x.append(Symbol('x2'))
    
    # 课本
    y = 2 * (x[0] - x[1] ** 2) ** 2 + (1 + x[1]) ** 2
    
    # Rosenbrock函数
    # y = 100 * (x[1] - x[0] ** 2) ** 2 + (1 - x[0]) ** 2
    
    return y

# 计算函数返回值
def cal_function_ret(function, x):
    res = function.subs([('x1', x[0]), ('x2', x[1])])
    return res

# 计算梯度
def cal_grad_ret(grad_function, x):
    res = []
    
    for i in range(len(x)):
        res.append(grad_function[i].subs([('x1', x[0]), ('x2', x[1])]))
    return res

# 海瑟矩阵定义
def Hessian_define(function):
    x = []
    x.append(Symbol('x1'))
    x.append(Symbol('x2'))
    H = zeros(2, 2)
    function = sympify([function])
    for i, fi in enumerate(function):
        for j, r in enumerate(x):
         for k, s in enumerate(x):
                H[j ,k] = diff(diff(fi, r), s)
    
    H = np.array(H)
    return H

#  海瑟矩阵计算
def cal_hessian_ret(hessian_function, x):
    res = []
    for i in range(2):
        temp = []
        for j in range(2):
            temp.append(hessian_function[i][j].subs([('x1', x[0]), ('x2', x[1])]))
        res.append(temp)      
    return res

# armijo-goldstein准则
def armijo_goldstein(function, grad_function, x0, d, c = 0.3):
    # 指定初始步长
    alpha = 1.0
    # 回退参数
    gamma = 0.333
    # 迭代次数
    k = 1.0

    # fd 表示 f(x + alpha * d)
    fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
    # fk 表示 f(x) + c * alpha * gradf(x) * d
    fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
    # fp 表示 f(x) + (1-c) * alpha * gradf(x) * d
    fp = cal_function_ret(function, x0) + (1-c) * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
    while fd > fk or fd < fp:
        alpha *= gamma
        fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
        fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
        fp = cal_function_ret(function, x0) + (1-c) * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
        k += 1.0
    print("迭代次数：", k)
    return alpha


# armijo-wolfe准则
def armijo_wlofe(function, grad_function, x0, d, c = 0.3):
    # wolfe准则参数
    c2 = 0.9
    # 指定初始步长
    alpha = 1.0
    # 二分法确定alpah
    a, b = 0, np.inf
    # 迭代次数
    k = 1.0
    
    # gk表示gradf(x)
    gk = cal_grad_ret(grad_function, x0)
    # fd 表示 f(x + alpha * d)
    fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
    # fk 表示 f(x) + c * alpha * gradf(x) * d
    fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
    # gp表示gradf(x + alpha * d)
    gp = cal_grad_ret(grad_function, np.add(x0, np.dot(alpha, d)))
    while True:
        if fd > fk:
            b = alpha
            alpha = (a + b) / 2
            fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
            fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
            gp = cal_grad_ret(grad_function, np.add(x0, np.dot(alpha, d)))
            k = k + 1
            continue
        if np.dot(gp, d) < c2 * np.dot(gk, d):
            a = alpha
            alpha = np.min(2 * alpha, (a + b) / 2)
            fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
            fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
            gp = cal_grad_ret(grad_function, np.add(x0, np.dot(alpha, d)))
            k = k + 1
            continue
        break
    return alpha

#  范数计算
def norm(x):
    return sqrt(np.dot(x, x))

# 牛顿法
def Newton(function, hessian_function ,grad_function, x0, delta):
    k = 0  # 迭代次数
    xk = x0  # 初始迭代点
    gk = cal_grad_ret(grad_function, xk)
    
    while norm(gk) > 0.00001 and k < 10000:
        gk2 = cal_hessian_ret(hessian_function, xk)  # 海瑟矩阵
        dk = np.dot(-1, np.dot(np.linalg.inv(np.array(gk2, dtype=float)), gk)) # 下降方向
        alpha = 0.01
        #  如果delta为0，利用wolf准则求步长
        if delta == 0:
            alpha = armijo_wlofe(function, grad_function, xk, dk)
        #  如果delta为1，利用glodstein准则求步长
        if delta == 1:
            alpha = armijo_goldstein(function, grad_function, xk, dk)
        xk = np.add(xk , np.dot(alpha, dk))  # 步长为1
        k = k + 1
        gk = cal_grad_ret(grad_function, xk)  # 更新梯度
        
    print("xk", xk)
    print("迭代次数", k)
    
    return cal_function_ret(function, xk)
            
if __name__ == '__main__':
    function = function_define()
    grad_function = cal_grad_funciton(function)
    Hessian_function = Hessian_define(function)
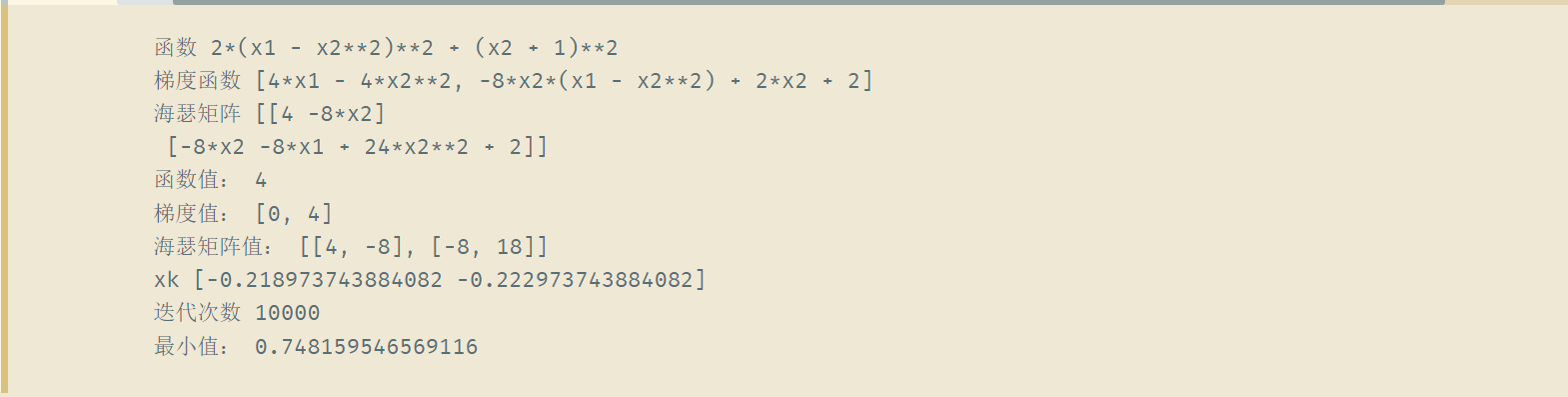
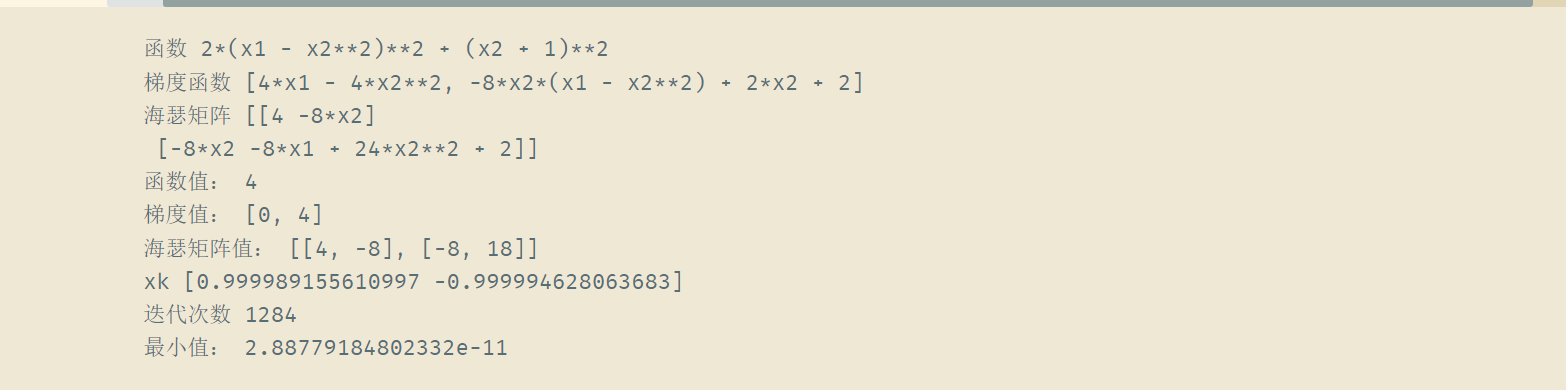
    print("函数", function)
    print("梯度函数", grad_function)
    print("海瑟矩阵", Hessian_function)
    
    #  计算(0, 0)处的函数值
    print("函数值：", cal_function_ret(function, [1, 1]))
    #  计算(0, 0)处的梯度值
    print("梯度值：", cal_grad_ret(grad_function, [1, 1]))
    #  计算(0, 0)处海瑟矩阵
    print("海瑟矩阵值：", cal_hessian_ret(Hessian_function, [1, 1]))
    #  
    print("最小值：", Newton(function, Hessian_function ,grad_function, [1, 1], 3))

在这里插入图片描述

三：拟牛顿法

拟牛顿法：牛顿法虽然收敛速度快，但是计算过程中需要计算目标函数的二阶偏导数计算复杂度较大，而且有时目标函数的海瑟矩阵无法保持正定，从而使得牛顿法失效，因此拟牛顿法提出用不含二阶导数的矩阵 $U_{t}$ 替代牛顿法中的 $H_{t}^{-1}$ ，然后沿搜索方向 $U_{t}g_{t}$ 做一维搜索，在“拟牛顿”的条件下优化目标函数不同的构造方法就产生了不同的拟牛顿法

（1）拟牛顿条件

拟牛顿条件：对海瑟矩阵的逆在做近似时不能随便乱来，需要一定的理论指导，而拟牛顿条件则是用来提供理论指导的，指出了用来近似的矩阵应该满足的条件

用 $B$ 表示对海瑟矩阵 $H$ 本身的近似，即 $B\approx H$
用 $D$ 表示对海瑟矩阵的逆 $H^{-1}$ 的近似，即 $B\approx H^{-1}$

设经过 $k + 1$ 次迭代后得到 $x_{k+1}$ ，此时将目标函数 $f (x)$ 在 $x_{k+1}$ 附近作泰勒展开，取二阶近似，得

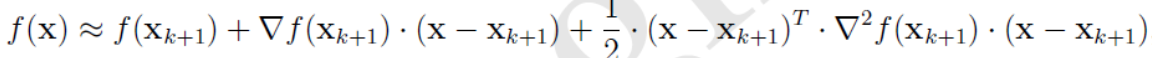
在这里插入图片描述

在上式两边同时作用一个梯度算子 $\nabla$ ，可得

$\nabla f(x) \approx \nabla f(x_{k+1})+H_{k+1}·(x-x_{k+1})$

上式中取 $x=x_{k}$ ，整理后可得

$g_{k+1}-g_{k}\approx H_{k+1}·(x_{k+1}-x_{k})$

引入记号

$s_{k}=x_{k+1}-x_{k},y_{k}=g_{k+1}-g_{k}$

则上式可写为

$y_{k}\approx H_{k+1}·s_{k}\quad ①$

或

$s_{k}\approx H_{k+1}^{-1}·y_{k}\quad ②$

$① ， ②$ 两式便是拟牛顿条件，它对迭代过程中的海瑟矩阵 $H_{k+1}$ 作约束，因此对 $H_{k+1}$ 做近似的 $B_{k+1}$ 以及对 $H^{-1}_{k+1}$ 做近似的 $D_{k+1}$ 可以将 $y_{k}= B_{k+1}·s_{k}$ 或 $s_{k}= D_{k+1}·y_{k}$ 作为指导

（2）DFP算法

DFP算法：是最早的拟牛顿法，会以以下迭代方法，对 $H_{k+1}^{-1}$ 作近似

$D_{k+1}=D_{k}+△ D_{k},\quad k=0,1, 2....$

$D_{0}$ 通常取为单位矩阵 $I$

其中校正矩阵 $D_{k}$

$D_{k}=\frac{s_{k}s_{k}^{T}}{s_{k}^{T}y_{k}}-\frac{D_{k}y_{k}y_{k}^{T}D_{k}}{y_{k}^{T}D_{k}y_{k}}$

其算法逻辑如下

在这里插入图片描述

import numpy as np
import math
from sympy import *

# 计算梯度函数
def cal_grad_funciton(function):
    res = []
    x = []
    x.append(Symbol('x1'))
    x.append(Symbol('x2'))
    for i in range(len(x)):
        res.append(diff(function, x[i]))
    return res

# 定义目标函数
def function_define():
    x = []
    x.append(Symbol('x1'))
    x.append(Symbol('x2'))
    
    # 课本
    y = 2 * (x[0] - x[1] ** 2) ** 2 + (1 + x[1]) ** 2
    
    # Rosenbrock函数
    # y = 100 * (x[1] - x[0] ** 2) ** 2 + (1 - x[0]) ** 2
    
    return y

# 计算函数返回值
def cal_function_ret(function, x):
    res = function.subs([('x1', x[0]), ('x2', x[1])])
    return res

# 计算梯度
def cal_grad_ret(grad_function, x):
    res = []
    
    for i in range(len(x)):
        res.append(grad_function[i].subs([('x1', x[0]), ('x2', x[1])]))
    return res

# 海瑟矩阵定义
def Hessian_define(function):
    x = []
    x.append(Symbol('x1'))
    x.append(Symbol('x2'))
    H = zeros(2, 2)
    function = sympify([function])
    for i, fi in enumerate(function):
        for j, r in enumerate(x):
         for k, s in enumerate(x):
                H[j ,k] = diff(diff(fi, r), s)
    
    H = np.array(H)
    return H

#  海瑟矩阵计算
def cal_hessian_ret(hessian_function, x):
    res = []
    for i in range(2):
        temp = []
        for j in range(2):
            temp.append(hessian_function[i][j].subs([('x1', x[0]), ('x2', x[1])]))
        res.append(temp)      
    return res

# armijo-goldstein准则
def armijo_goldstein(function, grad_function, x0, d, c = 0.3):
    # 指定初始步长
    alpha = 1.0
    # 回退参数
    gamma = 0.333
    # 迭代次数
    k = 1.0

    # fd 表示 f(x + alpha * d)
    fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
    # fk 表示 f(x) + c * alpha * gradf(x) * d
    fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
    # fp 表示 f(x) + (1-c) * alpha * gradf(x) * d
    fp = cal_function_ret(function, x0) + (1-c) * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
    while fd > fk or fd < fp:
        alpha *= gamma
        fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
        fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
        fp = cal_function_ret(function, x0) + (1-c) * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
        k += 1.0
    print("迭代次数：", k)
    return alpha


# armijo-wolfe准则
def armijo_wlofe(function, grad_function, x0, d, c = 0.3):
    # wolfe准则参数
    c2 = 0.9
    # 指定初始步长
    alpha = 1.0
    # 二分法确定alpah
    a, b = 0, np.inf
    # 迭代次数
    k = 1.0
    
    # gk表示gradf(x)
    gk = cal_grad_ret(grad_function, x0)
    # fd 表示 f(x + alpha * d)
    fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
    # fk 表示 f(x) + c * alpha * gradf(x) * d
    fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
    # gp表示gradf(x + alpha * d)
    gp = cal_grad_ret(grad_function, np.add(x0, np.dot(alpha, d)))
    while True:
        if fd > fk:
            b = alpha
            alpha = (a + b) / 2
            fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
            fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
            gp = cal_grad_ret(grad_function, np.add(x0, np.dot(alpha, d)))
            k = k + 1
            continue
        if np.dot(gp, d) < c2 * np.dot(gk, d):
            a = alpha
            alpha = np.min(2 * alpha, (a + b) / 2)
            fd = cal_function_ret(function, np.add(x0, np.dot(alpha, d))) 
            fk = cal_function_ret(function, x0) + c * alpha * np.dot(cal_grad_ret(grad_function, x0), d)
            gp = cal_grad_ret(grad_function, np.add(x0, np.dot(alpha, d)))
            k = k + 1
            continue
        break
    return alpha

#  范数计算
def norm(x):
    return math.sqrt(np.dot(x, x))

# 牛顿法
def Newton(function, hessian_function ,grad_function, x0, delta):
    k = 0  # 迭代次数
    xk = x0  # 初始迭代点
    gk = cal_grad_ret(grad_function, xk)
    
    while norm(gk) > 0.0001 and k < 10000:
        gk2 = cal_hessian_ret(hessian_function, xk)  # 海瑟矩阵
        dk = np.dot(-1, np.dot(np.linalg.inv(np.array(gk2, dtype=float)), gk)) # 下降方向
        alpha = 0.01
        #  如果delta为0，利用wolf准则求步长
        if delta == 0:
            alpha = armijo_wlofe(function, grad_function, xk, dk)
        #  如果delta为1，利用glodstein准则求步长
        if delta == 1:
            alpha = armijo_goldstein(function, grad_function, xk, dk)
        xk = np.add(xk , np.dot(alpha, dk))  
        k = k + 1
        gk = cal_grad_ret(grad_function, xk)  # 更新梯度
        
    print("xk", xk)
    print("迭代次数", k)
    
    return cal_function_ret(function, xk)

# 拟牛顿法（DFP）
def DFP_Newton(function, grad_function, x0):
    xk = x0
    
    alpha = 0.001 # 初始步长
    gk = cal_grad_ret(grad_function, xk)
    D = np.eye(2)  # 初始化正定矩阵 
    k = 1
    
    while k < 10000:
        dk = np.dot(-1, np.dot(D, gk)) # 下降方向
        xk_new = np.add(xk , np.dot(alpha, dk))  
        gk_new = cal_grad_ret(grad_function, xk_new)  # 更新梯度

        if norm(gk_new) < 0.0001:
            break
        
        # 计算y和s
        y = np.array(gk_new) - np.array(gk)
        s = np.array(xk_new) - np.array(xk)
        
        # 更新正定矩阵D
        D = D + np.dot(s, s.T)/np.dot(s.T, y) - np.dot(D, np.dot(y, np.dot(y.T, D))) / np.dot(y.T, np.dot(D, y))
        
        k = k + 1 
        
        gk = gk_new  
        xk = xk_new  # 更新xk
        
    print("xk", xk)
    print("迭代次数", k)
    
    return cal_function_ret(function, xk)

if __name__ == '__main__':
    function = function_define()
    grad_function = cal_grad_funciton(function)
    Hessian_function = Hessian_define(function)
    print("函数", function)
    print("梯度函数", grad_function)
    print("海瑟矩阵", Hessian_function)
    
    #  计算(0, 0)处的函数值
    print("函数值：", cal_function_ret(function, [1, 1]))
    #  计算(0, 0)处的梯度值
    print("梯度值：", cal_grad_ret(grad_function, [1, 1]))
    #  计算(0, 0)处海瑟矩阵
    print("海瑟矩阵值：", cal_hessian_ret(Hessian_function, [1, 1]))
    #  
    print("最小值：", DFP_Newton(function, grad_function, [1, 1]))