堆排序过程:

>建立堆(大根堆)

>得到堆顶元素，为最大元素

>去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整使堆重新有序

>堆顶元素为第二大元素

>重复步骤3，直到堆变空

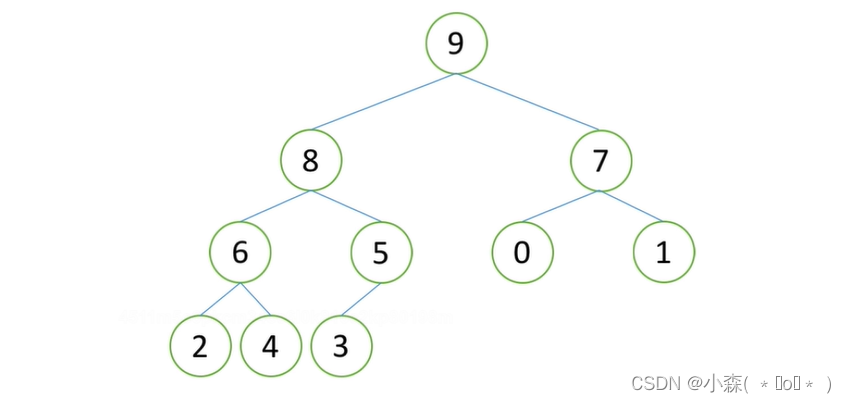
 此时是建立堆后的大根堆模型

将9拿下来，为了节约内存，提高利用率，可以将9放到3(最后一个元素)，然后3放到堆顶，再此经过调整，3放到合适的位置并且除了9的最大元素又被调到堆顶。

每次经过调整，整个堆的最后几个元素不断形成有序区，即，大根堆在不断变小

首先我们要调整一个无序列表等成为一个大根堆(先将列表看成一个堆)

 我们要从最末尾开始调整，才能保证大元素一步步被调上去

 

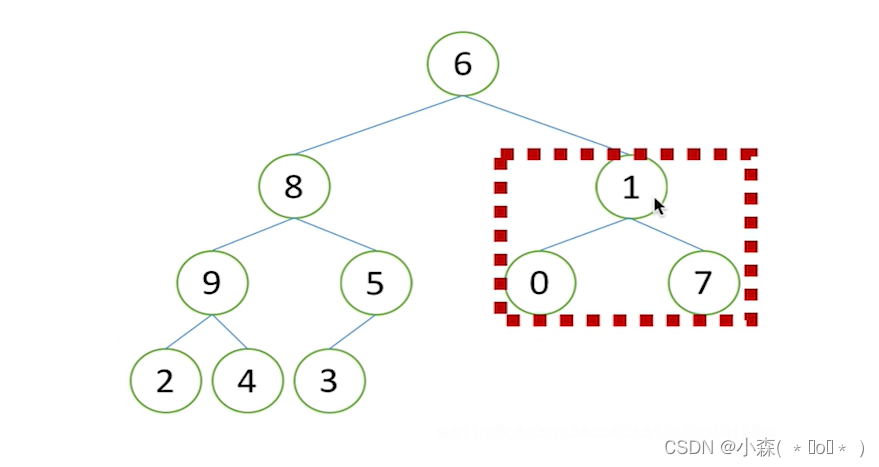
 我们可以看出是从最后一个元素的根节点开始调整，即5，9，1...

列表长为n=len(li)，所以5的下标为(n-2)//2

我们可以先写调整部分的代码：

def sift(li,low,high):   # 堆的第一个元素和最后一个元素
    i=low
    j=2*i+1       # j刚开始是左孩子
    tmp=li[low]   # 把堆顶存起来
    while j<=high: # 只要j位置有数,没有越界
        if j+1<=high and li[j+1]>li[j]:   # 保证右孩子不越界,因为最右侧列表是有序区,不是堆
            j=j+1    # j指向右孩子          # 与左右孩子对比前,先左右孩子比较
        if li[j]>tmp:
            li[i]=li[j]
            i=j
            j=2*i+1
        else:
            li[i]=tmp
            break
    else:
        li[i]=tmp  # 到最后了,通过计算左孩子已经超出high了

堆排序的代码：

def heap_sort(li):
    n=len(li)
    for i in range((n-2)//2,-1,-1):   # 倒着走,一直往左遍历,第一个元素的前一个元素就是-1下标
        # i表示建堆时调整的部分的根的下标
        sift(li,i,n-1)   # 避免麻烦直接选最后,high作用只有一个就是确定别越界
    print(li)
    # 建堆完成了
    for i in range(n-1,-1,-1):     # 一直确定堆最后元素
        # i一直指向当前堆的最后一个元素
        li[0],li[i]=li[i],li[0]
        sift(li,0,i-1)

实验代码:

li=[i for i in range(12)]
random.shuffle(li)
print(li)

heap_sort(li)
print(li)

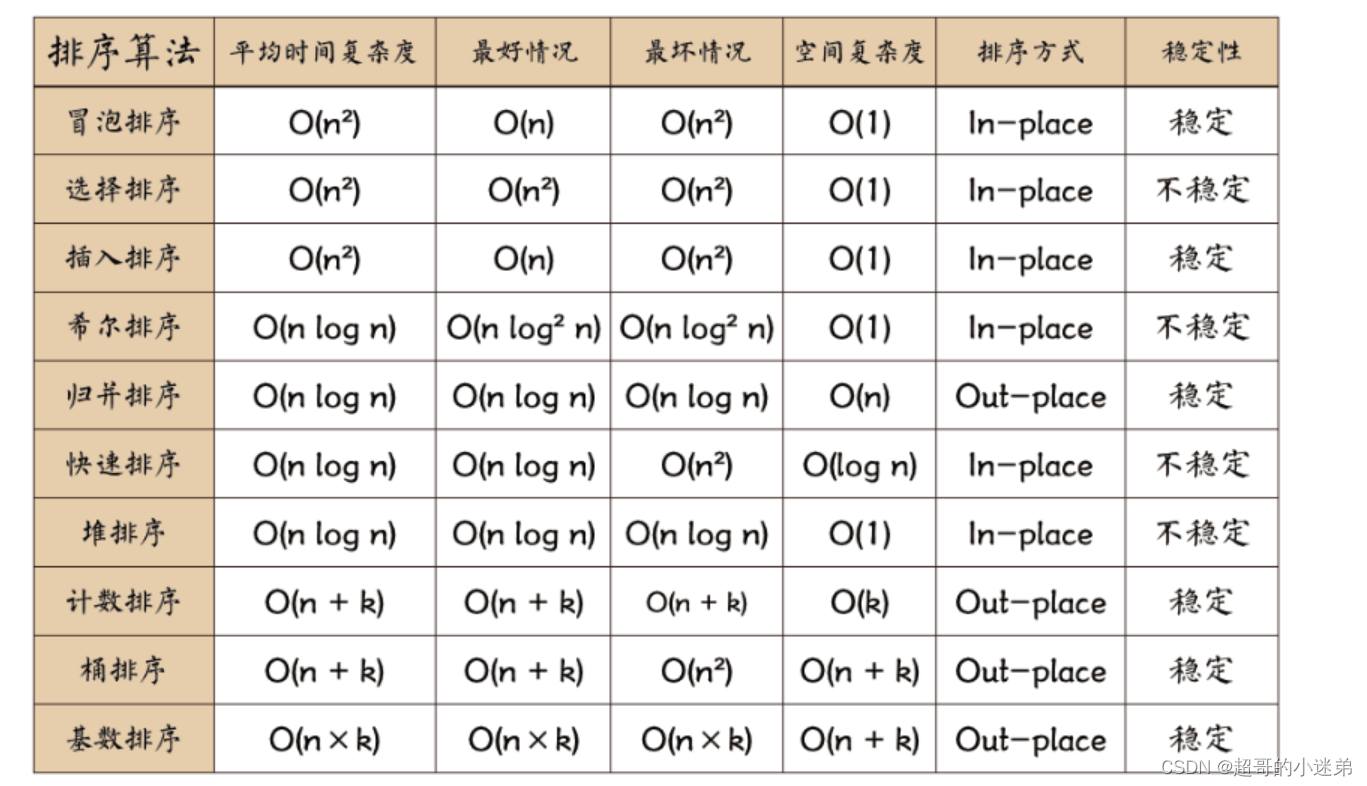
可以看出堆排序时间复杂度为O(nlogn)

当然python内部也有堆的内置模块

import heapq
import random

li=list(range(12))
random.shuffle(li)

print(li)

heapq.heapify(li)   # 默认建立小根堆
n=len(li)
for i in range(n):
    print(heapq.heappop(li))   # 每次弹出一个元素