一、初窥其貌
1.1 启发式算法和元启发式算法
启发式算法是求解优化问题的一类方法,因为经典优化方法存在局限性,有时无法得到最优解,只能得到一个可以接受的近似最优解,启发式算法就适合求解这类问题。启发式算法就是专家的推测,借助过去经验的归纳推理,以期求得问题的近似最优解或以一定概率求得最优解,所以认为启发式算法是基于经验或者实验算法的统称。
元启发式算法则是从自然界的一些现象中获得灵感,通过这些现象的特点解决实际问题,如模拟退火算法、遗传算法等。
启发式算法 = 元启发式算法 + 问题特征
1.2 局部最优与全局最优
下图是说明局部最优和全局最优的典型例子,绿色点是局部最优,红色点是全局最优。
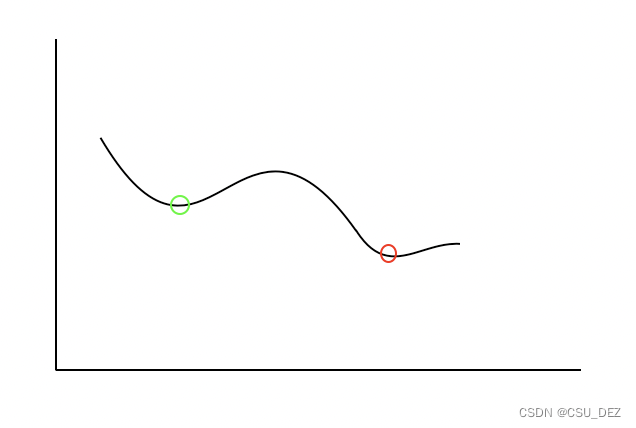
如果采用局部最优算法,从左到右寻找最小值点,到达绿色点时,算法认为已经找到最优,因为它无法忍受在继续尝试的过程中使值反而变大,绿色点左右两侧的值都比它大,算法无法跳出局部最优的情况。
如果采用全局最优算法,从左到右寻找最小值点,达到绿色点时,算法仍有机会跳出该点,因为算法允许情况有一定概率发生恶化,即允许下一次尝试的值比绿色点的值大。当尝试的值翻过绿点右侧的山丘(极大值)时,则可以找到全局最优的红点。
二、模拟退火
2.1 灵感来源
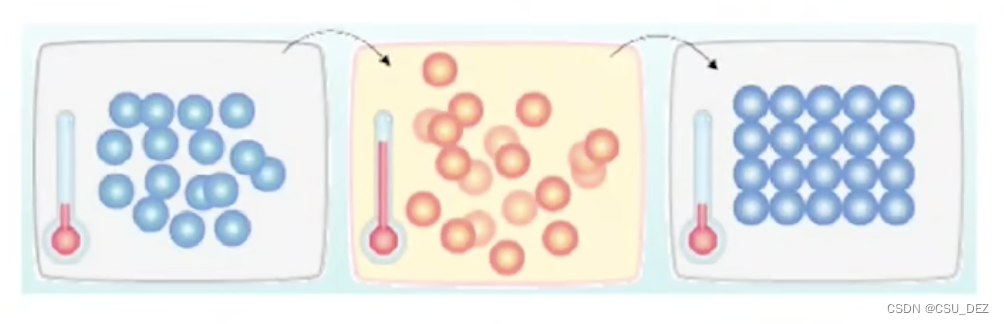
退火是冶金行业的术语,指的是将金属加热到一定温度后,以适宜速度冷却(通常较为缓慢),若以较快速度冷却则称为淬火。自然界中的物质,温度越高能量越大,温度越低能量越小,而采取缓慢冷却的方式通常可以达到最低能量状态,模拟退火就是从该现象得到的启发。
2.2 算法思想
模拟退火(Simulated-Annealing, SA)算法的思想概括如下:
- 若目标函数由第 i 步移动到第 i + 1 步后的结果更优,即 f(Y( i + 1 )) <= f(Y(i)),总是接受该移动。
- 若没有,即 f(Y( i + 1 )) > f(Y(i)),则以一定概率接受该移动,且该概率随着时间推移逐渐变小。
模拟退火期望得到的是全局最优解,因此它可以容忍结果以一定概率发生恶化,这个概率的计算采用的是 Metropolis 准则。
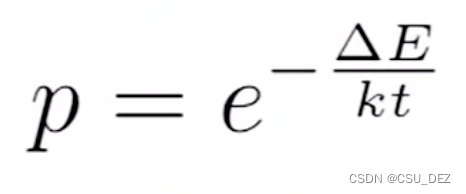
k 为常数,t 表示温度,delta E 为两次结果的能量差值,p 为接受较差结果的概率。其它参数相同时,温度较高,即 t 较大,p 的值较大;温度较低,即 t 较小,p 的值较小。说明在算法开始阶段,接受差结果的概率较大,随着时间推移温度降低,为了稳定于某个值,接受差结果的概率变小。
2.3 算法流程图
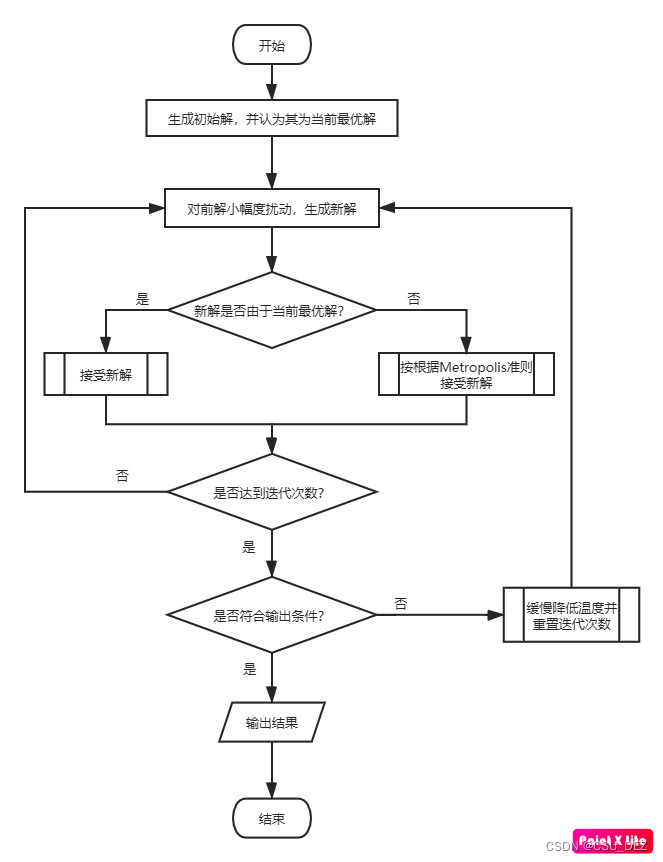
(非本人所做,侵删)
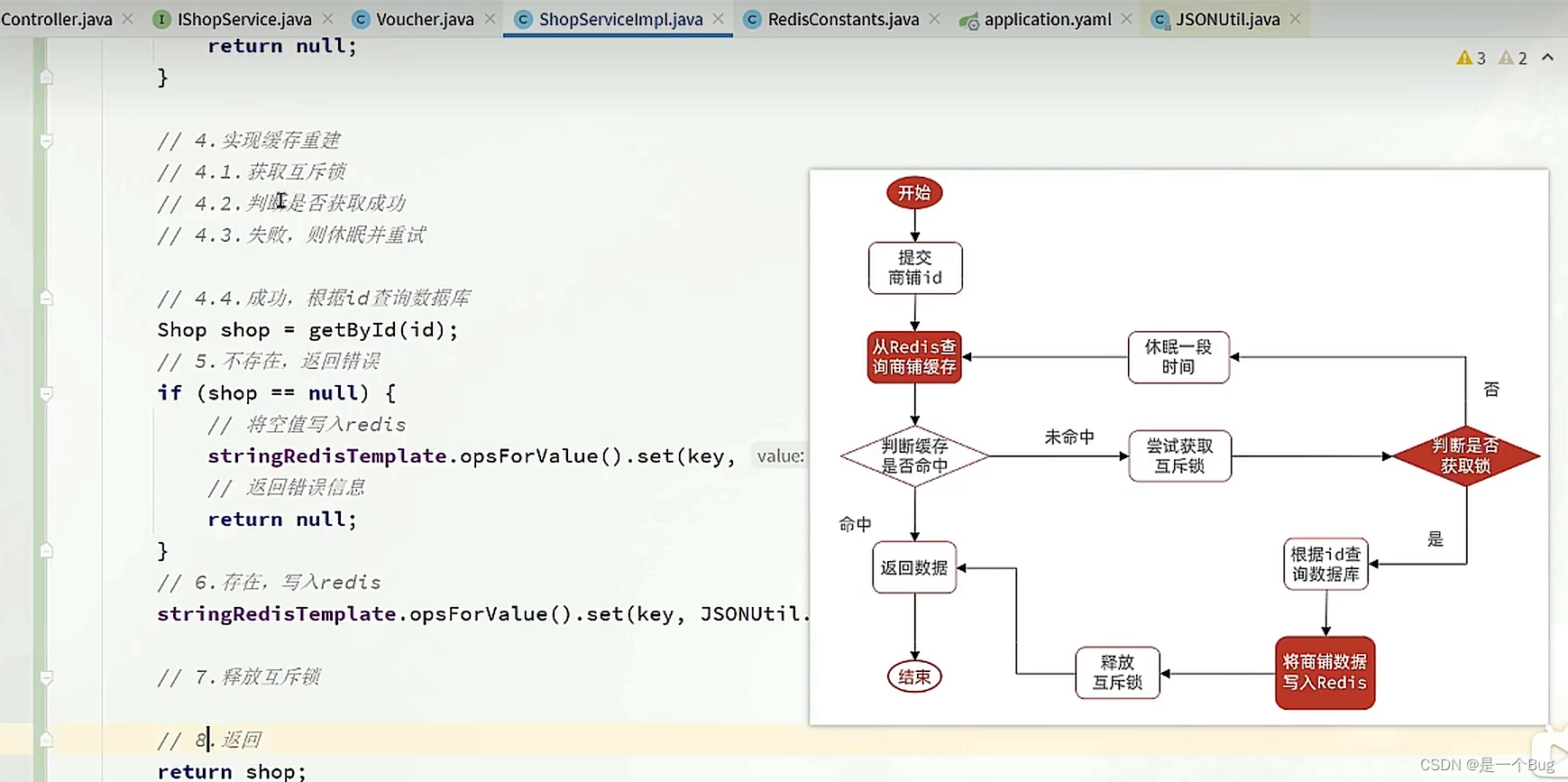


![[附源码]计算机毕业设计港口集团仓库管理系统Springboot程序](https://img-blog.csdnimg.cn/fcd06f6f2ef149a6b11440f5555f4000.png)

![[附源码]Node.js计算机毕业设计电商后台管理系统Express](https://img-blog.csdnimg.cn/b2e4bac576bb428d8f529f547a7e13e5.png)