第一课: 《编译原理求语法树的短语和直接短语等等》
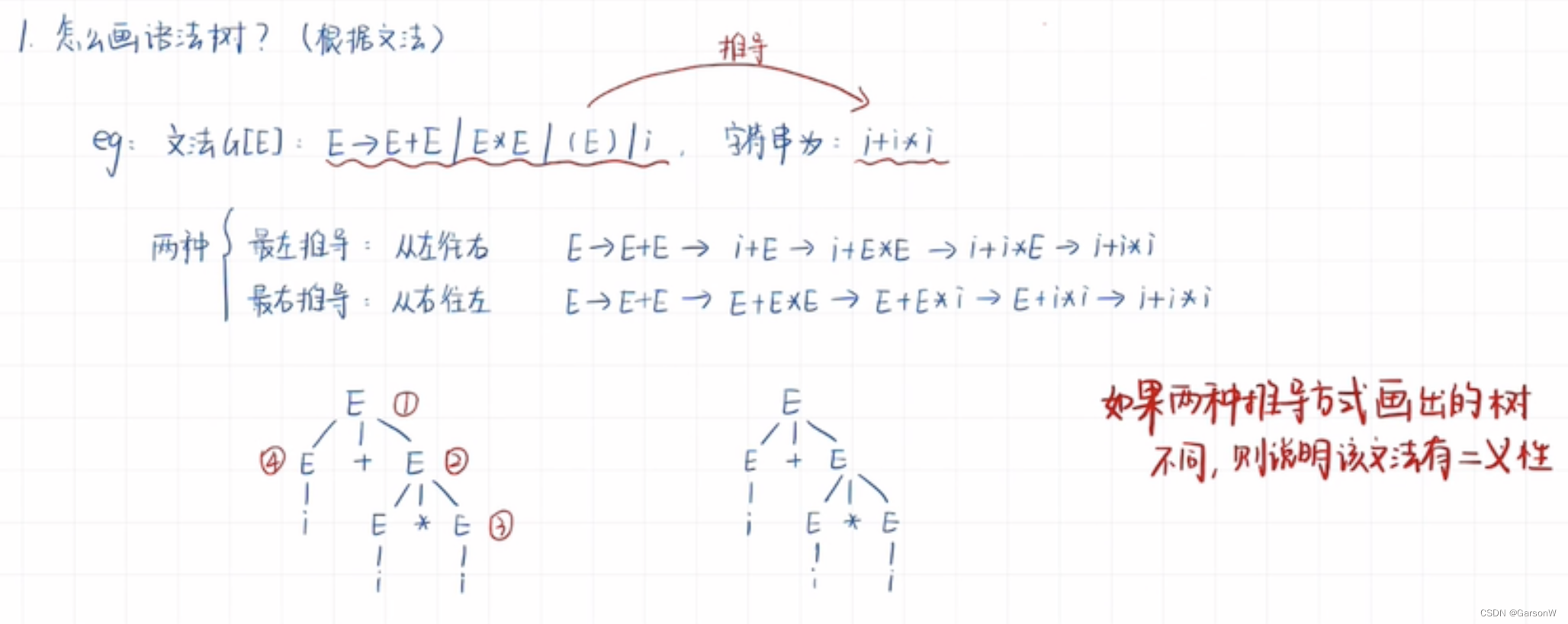
二义性是什么?
如果最左推导和最右推导的结果不一致,那么说明文法有二义性
短语是什么?
找短语就是找能长叶子的结点,有五个如图圆圈标号1 2 3 4 5
直接短语(简单短语):说简单点就是一个孩子一个爹,本题中的i
素短语:在短语中找,至少含有一个终结符,且不含其他更小素短语
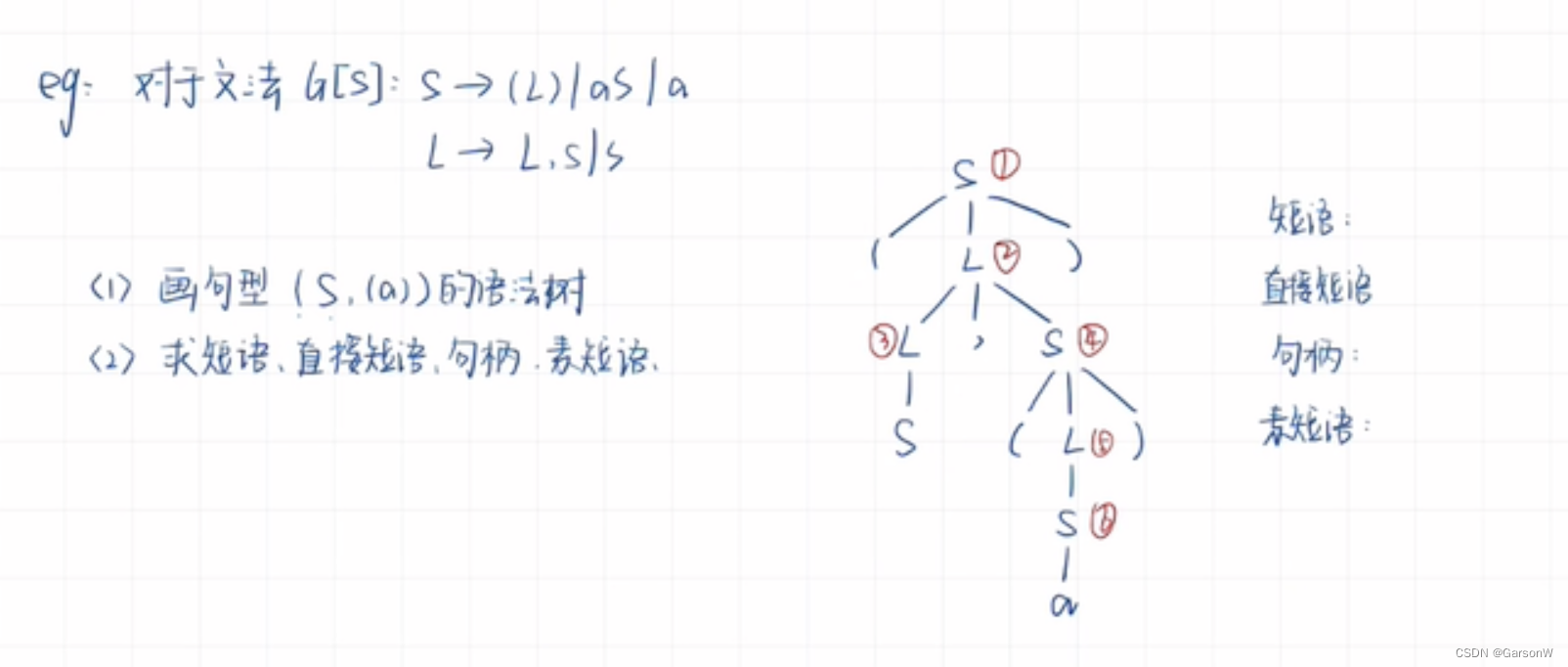
例题:
画出语法树:
短语:就是非叶子结点生成的叶子结点。
直接短语就是:一个孩子一个爹,这里是S、a
句柄就是:在树最左边的直接短语,那就是S
第二课:《消除左递归消除回朔的方法》
消除左递归:
先将后面的B往前提,然后新建一个A‘,然后A’->除了A的所有往前移A‘/空串
如果不是本文法的则不是左递归,直接写即可。
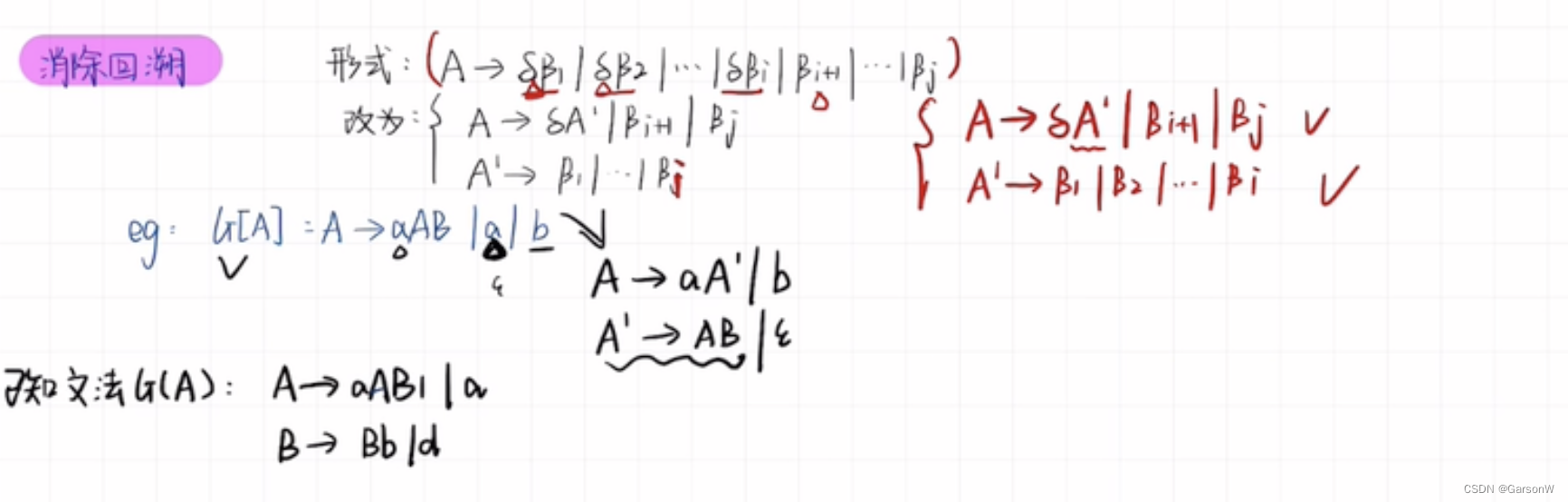
消除回溯:
含公共左因子a的提出来,然后给一个A‘,如果不含则不提。
A‘->(除了公共因子a的所有)/(如果只有a就是空串)/(没有a的已经在上一部提出,不用再写)
例题:
第一条为回溯,第二条为坐递归。答案为蓝色字体
第三课:《如何求First集和Follow集》
如何求FIRST集和FOLLOW集?
First集看的是产生式的左边,Follow集看的是产生式的右边。
FIRST集如何写?
看产生式的左边:1.如果是终结符就直接写 2.如果是非终结符就到该产生式中去找
较为复杂的FIRST集的解决
FOLLOW集如何写?
看产生式的右边:有以下三步
(1) 若B后为空,则将产生式右边的FOLLOW(A)集加入FOLLOW(B)集
(2) 若B后不为空:
后面跟着终结符:终结符直接加入FOLLOW(B)集中
后面跟着非终结符:将非终结符的FIRST集加入FOLLOW(B)集中
⚠️如果跟着非终结符能推出的是空的话,那又回到了(1)的情况来解决
例题:
课上练习:《LL(1)文法》
怎么求LL(1)文法?
(1)消除左递归,消除回溯
(2)写出改造后的文法G'(A)
(3)写出FIRST集,FOLLOW集
(4)构造G‘(A)的LL(1)分析表
如何判断是否为LL(1)文法?
我们要分析改造后的文法中G'(A)的产生式中能产生两项的式子。
如下,A产生a/B:
如果B不是空串,且FIRST集不相交,则为LL(1)文法;
如果B为空串,且FIRST(a)集与FOLLOW(A)不相交,则为LL(1)文法;
判断是否为LL(1)文法的例子:
改造文法:
判断过程:
两个产生式的B都是空串,所以比较公式为:
产生式右边第一项的FIRST集和产生式左边的FOLLOW集。
(1)对于A‘->AB1/空 比较FIRST(A)与FOLLOW(A')不相交✅
(2)对于B‘->bB'/空 比较FIRST(b)与FOLLOW(B')不相交✅
结论:
为LL(1)文法。









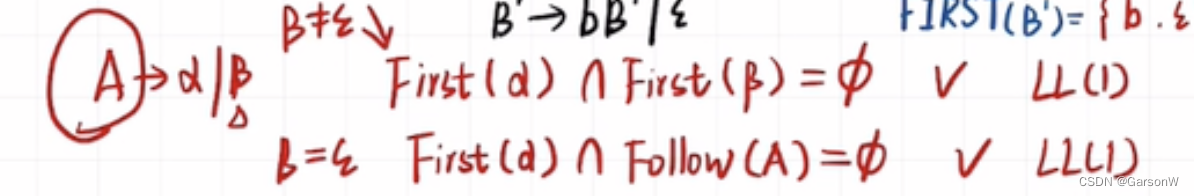


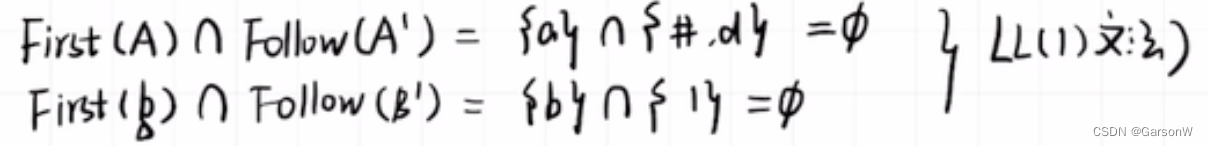

![[附源码]计算机毕业设计港口集团仓库管理系统Springboot程序](https://img-blog.csdnimg.cn/fcd06f6f2ef149a6b11440f5555f4000.png)

![[附源码]Node.js计算机毕业设计电商后台管理系统Express](https://img-blog.csdnimg.cn/b2e4bac576bb428d8f529f547a7e13e5.png)




![[1.2.0新功能系列:二] Apache Doris 1.2.0 JDBC外表 及 Mutil Catalog](https://img-blog.csdnimg.cn/img_convert/89057697ab6d9a07f92e99a8dfad955b.png)