关联分析-Apriori

1. 定义

关联分析就是从大规模数据中，发现对象之间隐含关系与规律的过程，也称为关联规则学习。

2. 相关概念

2.1 事务、项与项集

订单号	购买商品
0001	可乐、薯片
0002	口香糖、可乐
0003	可乐、口香糖、薯片

以上面的订单为例：

• 事务：每条交易记录可称为一个事务。上面的订单中包含3个事务。
• 项：指我们分析数据中的对象（物品）。上面3条交易记录中共包含3个项（可乐、薯片、口香糖）。
• 项集：指由若干项构成的集合，k 个项组成的项集，叫 k 项集。

2.2 支持度

某项集在事务中出现的频率。即项集在事务中出现的次数除以事务总数。
$$support(A)=\frac{count(A)}{count(dataset)}=P(A)$$
支持度体现的就是某项集的出现频率，只有某项集的支持度达到一定程度，才有研究该项集的必要。

2.3 置信度

关联规则$(A\to B)$中，$A$与$B$同时出现的次数，除以$A$出现的次数。表示$A$发生的前提下,$B$发生的概率。
$$\begin{gathered} confidence(A\to B)=\frac{count(AB)}{count(A)} \\ =\frac{count(AB)/count(dataset)}{count(A)/count(dataset)} \\ =\frac{P(AB)}{P(A)} \\ =P(B|A) \end{gathered}$$
置信度体现的时关联规则的可靠程度。若关联规则$(A\to B)$的置信度较高，则说明当$A$发生时，$B$也有很大概率发生。

2.4 提升度

关联规则$(A\to B)$中，提升度是指$(A\to B)$的置信度除以$B$的支持度
$$lift(A\to B)=\frac{confidence(A\to B)}{support(B)}=\frac{P(AB)}{P(A)P(B)}$$
提升度体现的是组合（应用关联规则）相对不组合（不应用关联规则）的比值。

• 若提升度大于1，则说明该关联规则是有价值的，起促进作用；

• 若提升度等于1，表示管理那规则不产生影响；

• 若提升度小于1，说明应用该关联规则起到了负面影响。

因此应尽可能让关联规则的提升度大于1，提升度越大，则应用该关联规则的效果越好。

2.5 频繁项集

通常，我们仅对频繁出现的项集进行研究。因此，我们会设计一个支持度阈值，若一个项集的支持度大于等于该阈值，则该项集就称为频繁项集。若频繁项集中含有k个元素，则称其为频繁k项集。

3. 关联分析过程

关联分析可分为如下两个过程：

1. 从数据集中寻找频繁项集
2. 从频繁项集中生成关联规则

3.1 寻找频繁项集

首先，我们需要能够找到所有的频繁项集，即经常出现在一起的对象集合。一般只要按如下步骤来进行即可 :

1. 遍历对象之间所有可能的组合(包括单个对象的组合)，每种组合构成一个项集
2. 针对每一个项集A，计算A的支持度(A出现的次数除以记录总数)。
3. 返回所有支持度大于指定阈值的项集。

上面的订单的频繁项集如下：

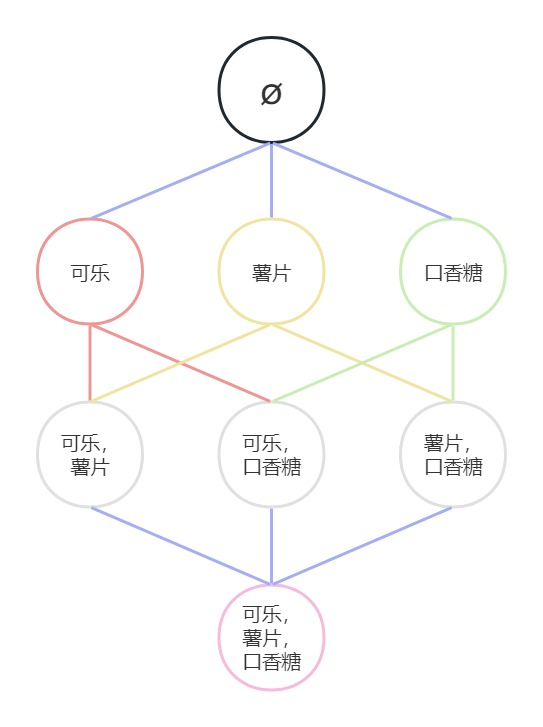
上面寻找频繁项集的方法，理论上是没有问题的，但却很难在实际应用中使用。如，在上图中，3个不同
的对象(项)，可以构成8种组合。而对于含有$N$个对象的数据集，总共可以构成$2^N-1$种组合。当$N$比较大时，计算量就会按指数级增长。

因此，为了降低计算量，我们使用Apriori算法进行优化。Apriori算法的原理如下：

1. 如果一个项集是频繁项集，则其所有子集(非空)也是频繁项集
2. 如果一个项集(非空)是非频繁项集，则其所有父集也是非频繁项集

Apriori算法会从$k=1$开始，使用两个$k$项集进行组合，从而产生$k+1$项集。结合之前介绍的算法原理可知，频繁$k+1$项集是由两个$k$项集组合而成的，而对于频繁$k+1$项集来说，其所有$k$项集的子集必然都是频繁项集，这就意味着，频繁$k+1$项集只可能由两个频繁$k$项集组合产生。因此，在组合的过程中，一旦发现某个$k$项集不是频繁项集(支持度小于指定的阈值)，就可以将其移除，而无需再参与后续生成$k+1$项集的组合。这样一来，就可以大大减少计算量。

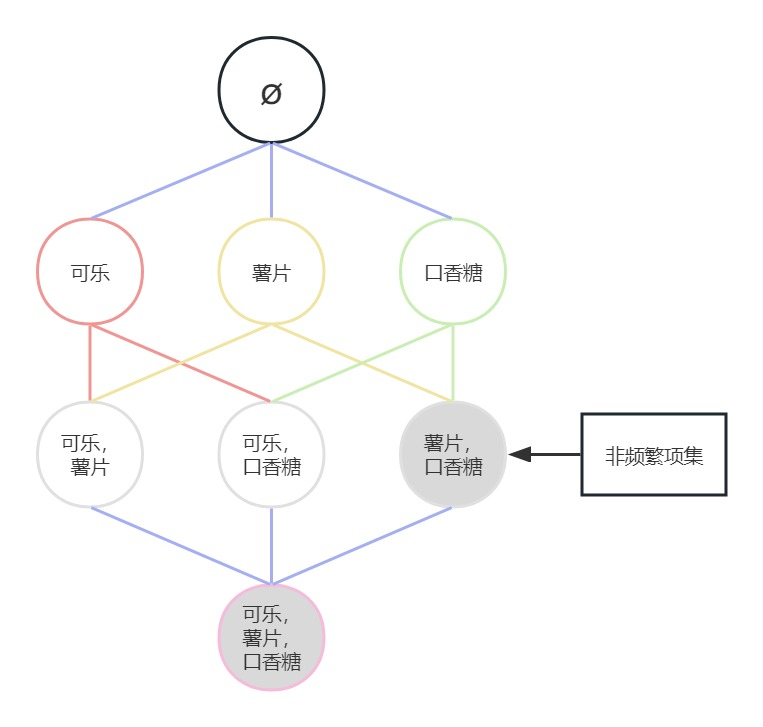
例如在上图中，假设（薯片，口香糖）是非频繁项集，则根据Apriori算法，其所有父集也是非频繁项集，故（可乐，薯片，口香糖）也是非频繁项集。因此，我们就没有必要使用（薯片，口香糖）与其他2项集进行组合去生成3项集了，因为生成的3项集（可乐，薯片，口香糖）也是非频繁项集。

3.2 Apriori算法流程

Apriori算法是第一个关联规则挖掘算法，它利用逐层搜索的迭代方法找出数据库中项集的关系，以形成规则，其过程由连接（类矩阵运算）与剪枝（去掉那些没必要的中间结果）组成。该算法中项集的概念即为项的集合。包含k个项的集合为k项集。项集出现的频率是包含项集的事务数，称为项集的频率。如果某项集满足最小支持度，则称它为频繁项集。

Apriori算法流程如下：

1. 扫描数据集，从数据集中生成候选$k$项集$C_k$（$k$从1开始）。

2. 计算$C_k$中，每个项集的支持度，删除低于阈值的项集，构成频繁项集$L_k$。

3. 将频繁项集$L_k$中的元素进行组合，生成候选$k+1$项集$C_{k+1}$

4. 重复步骤2、3，直到满足以下两个条件之一时，算法结束

   • 频繁项集无法组合生成更大的候选项集

   • 所有的候选项集支持度都低于指定的阈值（最小支持度)，无法生成频繁项集

说明：这里的$C_k$是指所有的候选$k$项集，$L_k$是指所有的频繁$k$项集。

4. 生成关联规则

当产生频繁项集后，生成关联规则会相对简单，我们只需要将每个频繁项集拆分成两个非空子集，然后就可以使用这两个子集构成关联规则。当
然，一个频繁项集拆分成两个非空子集可能有很多种方式，我们要考虑每一种不同的可能。例如，频繁项集 { 1 , 2 , 3 } \{1,2,3\} {1,2,3}可以生成如下6个关联规则：
{ 1 → 2 , 3 } \{1\rightarrow2,3\} {1→2,3}
{ 2 → 1 , 3 } \{2\rightarrow1,3\} {2→1,3}
{ 3 → 1 , 2 } \{3\rightarrow1,2\} {3→1,2}
{ 1 , 2 → 3 } \{1,2\rightarrow3\} {1,2→3}
{ 1 , 3 → 2 } \{1,3\rightarrow2\} {1,3→2}
{ 2 , 3 → 1 } \{2,3\rightarrow1\} {2,3→1}
然后，针对每个关联规则，分别计算其置信度，仅保留符合最小置信度的关联规则。

5. 代码实现

数据下载：

链接：https://pan.baidu.com/s/1OSHupRjmHmMv3F0rwRwnpQ?pwd=fhh6
提取码：fhh6

import pandas as pd
import itertools

# 加载数据集
def load_data(path):
    result = []
    with open(path) as f:
        for line in f:
            line = line.strip("\n")
            result.append(line.split(","))
    return result


# 生成候选1项集列表
# 接下来，扫描加载后的数据集，生成候选1项集列表。
# 因为候选1项集列表是从原始数据集中生成的，因此，
# 列表中的每个元表就是数据集中不重复的对象。
# 为了方便后面的操作，将每个对象放入frozenset中。
# 将每个对象放入frozenset而不是set中，
# 是为了将元素作为字典的key
def buildC1(dataset):
    item1 = set(itertools.chain(*dataset))
    return [frozenset([i]) for i in item1]



def ck_to_lk(dataset, ck, min_support):
    """根据候选k项集与对应的最小支持度，创建生成频繁k项集

    """
    # 定义项集-频数字典
    support = {}
    for row in dataset:
        for item in ck:
            # 判断项集是否在记录中出现
            if item.issubset(row):
                support[item] = support.get(item, 0) + 1
    total = len(dataset)
    return {k: v / total for k, v in support.items() if v / total >= min_support}

# 频繁k项集组合成候选k+1项集

# 当产生频繁K项集之后，需要对频繁k项集中的元素进行组合
# 如果组合后的项集数量为k +1，则保留此种组合，
# 否则，丢弃此种组合。
def lk_to_ck(lk_list):
    """根据参数指定的频繁k项集，组合生成候选k+1项集

    """

    # 保存所有组合之后的候选k+1项集
    ck = set()
    lk_size = len(lk_list)
    # 如果频繁k项集的数量不大于1，
    # 则不可能再通过组合生成候选k+1项
    # 直接返回空set即可
    if lk_size > 1:
        # 获取频繁k项集的k值
        k = len(lk_list[0])
        # 获取任意两个元素序号的索引组合
        for i, j in itertools.combinations(range(lk_size), 2):
            # 将对应位置的两个频繁k项集进行组合，生成一个新的项集
            t = lk_list[i] | lk_list[j]
            # 若组合后的项集时k+1项集，则为候选k+1项集，加入到set中
            if len(t) == k + 1:
                ck.add(t)
    return ck




# 生成所有频繁项集
def get_L_all(dataset, min_support):
    """根据最小支持度，从指定的数据集中，返回所有的频繁项集

    """
    c1 = buildC1(dataset)
    L1 = ck_to_lk(dataset, c1, min_support)
    # 定义字典，保存所有的频繁k项集
    L_all = L1
    Lk = L1
    # 当频繁项集字典中的元素数量大于1时，才有可能组合生成候选k+1项集
    while len(Lk) > 1:
        lk_key_list = list(Lk.keys())
        # 由频繁k项集生成候选k+1项集
        ck = lk_to_ck(lk_key_list)
        # 由候选k+1项集组合生成频繁k+1项集
        Lk = ck_to_lk(dataset, ck, min_support)
        # 若频繁k+1项集字典不为空，则将所有频繁k+1项集加入到L_all字典中
        if len(Lk) > 0:
            L_all.update(Lk)
        else:
            # 频繁k+1项集为空，退出循环
            break
    return L_all



# 生成关联规则
def rules_from_item(item):
    """从指定的频繁项集中生成关联规则

    """
    # 定义规则左侧的列表
    left = []
    for i in range(1, len(item)):
        left.extend(itertools.combinations(item, i))
    return [(frozenset(le), frozenset(item.difference(le))) for le in left]

"""
当生成包含所有频繁K项集的字典后，我们就可以遍历字典中的每一个频繁项集，进而计算该频繁项集的所有可能的关联规则，然后对每一个可能的关联规则，计算置信度，保留符合最小置信度的关联规则。
"""


def rules_from_L_all(L_all, min_confidence):
    """从所有频繁项集字典中生成关联规则列表

    """
    # 保存所有候选的关联规则
    rules = []
    for Lk in L_all:
        # 若频繁项集的元素个数为1，则无法生成关联规则，不予考虑
        if len(Lk) > 1:
            rules.extend(rules_from_item(Lk))
    result = []
    for left, right in rules:
        support = L_all[left | right]
        confidence = support / L_all[left]
        lift = confidence / L_all[right]
        if confidence >= min_confidence:
            result.append({"左侧": left, "右侧": right, "支持度": support, "置信度": confidence, "提升度": lift})
    return result

def apriori(dataset ,min_support, min_confidence):
    L_all = get_L_all(dataset,min_support)
    rules = rules_from_L_all(L_all, min_confidence)
    return rules

# 将对象的编号转换成名称
def change(item):
    li = list(item)
    for i in range(len(li)):
        li[i] = index_to_str[li[i]]
    return li

if __name__=="__main__":
    dataset = load_data("data.csv")
    # print(dataset)

    # 编码转换
    # 对原始数据进行转换，将字符串映射为索引

    items = set(itertools.chain(*dataset))
    str_to_index = {}
    index_to_str = {}
    for index, item in enumerate(items):
        str_to_index[item] = index
        index_to_str[index] = item
    # 输出结果#
    # print("字符串到编号:", list(str_to_index.items())[:5])
    # print("编号到字符串:", list(index_to_str.items())[:5])

    for i in range(len(dataset)):
        for j in range(len(dataset[i])):
            dataset[i][j] = str_to_index[dataset[i][j]]
    # print(dataset)
    
    rules = apriori(dataset, 0.05, 0.3)

    df = pd.DataFrame(rules)
    df = df.reindex(["左侧", "右侧", "支持度", "置信度", "提升度"], axis=1)
    df["左侧"] = df["左侧"].apply(change)
    df["右侧"] = df["右侧"].apply(change)
    print(df)

参考资料

1. https://edu.csdn.net/learn/36761/565907?spm=3001.4143
2. https://blog.csdn.net/weixin_53823523/article/details/119845775
3. https://baike.baidu.com/item/APRIORI/2000746?fr=ge_ala