一、树的概念
1.1 空树和非空树
空树:结点数为0的树
非空树:有且仅有一个根节点。其中,没有后继的结点叫叶子结点,有后继的结点叫做分支结点。
如下图所示:

1.2树的属性
除了根结点外任何一个结点都有且仅有一个前驱
树的高度:总共多少层
结点的深度:从上往下数
结点的度:即有几个分支,叶子结点的度是0,非叶子结点的度>0
树的度:各结点的度的最大值
二、二叉树的概念
2.1 二叉树的介绍
二叉树是n个结点的有限集合:
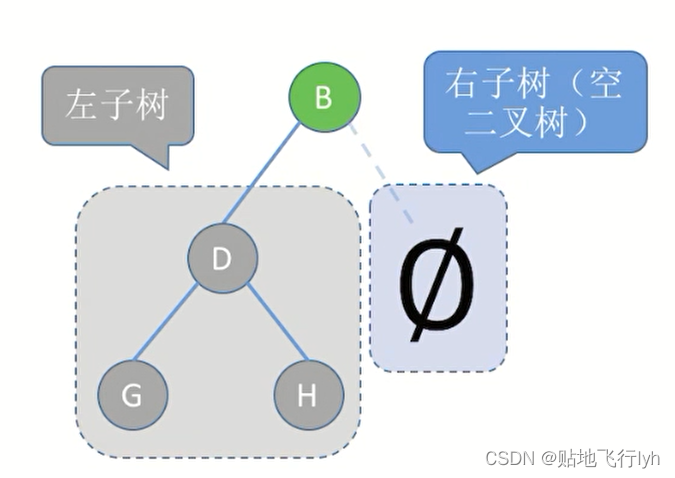
①或者为空二叉树,即n = 0。
②或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
特点:①每个结点至多只有两棵子树
②左右子树不能颠倒(二叉树是有序树)
2.2 二叉排序树的介绍
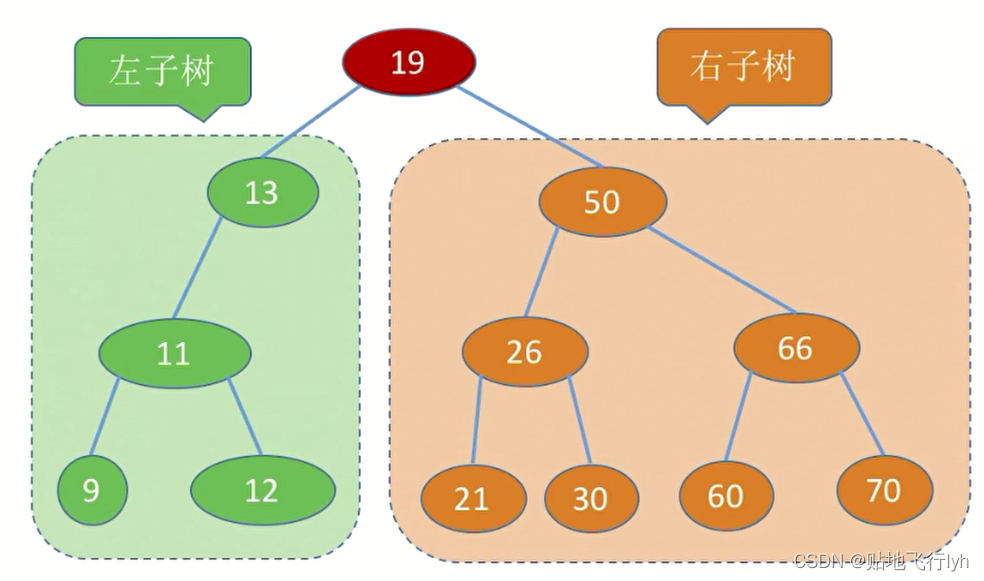
二叉排序树:一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:
左子树上所有结点的关键字均小于根结点的关键字,
右子树上所有结点的关键字均大于根结点的关键字。
左子树和右子树又各是一棵二叉排序树。
2.3 平衡二叉树的引入
平衡二叉树:树上任一结点的左子树和右子树的深度之差不超过1。它可以在插入和删除节点时自动调整树的结构,使得树的高度保持在一个较小的范围内,从而提高了树的查找、插入和删除的效率。在数据库中,索引是一种用于加速数据检索的数据结构。平衡二叉树可以用来实现数据库的索引,它可以快速地定位到需要查找的数据,从而提高了数据库的查询效率。
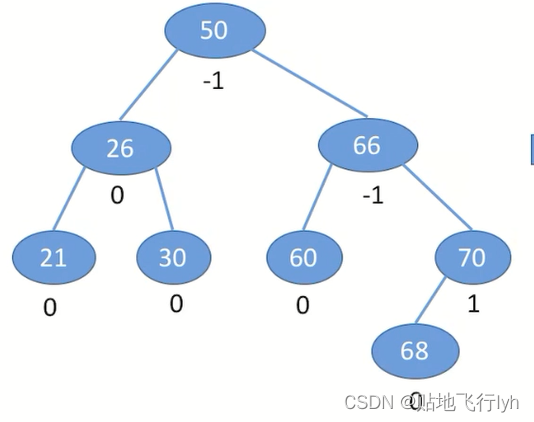
其中,结点的平衡因子=左子树高-右子树高,故平衡二叉树中结点的平衡因子只可能是1,-1,0。
2.3.1 调整最小不平衡子树(LL型)
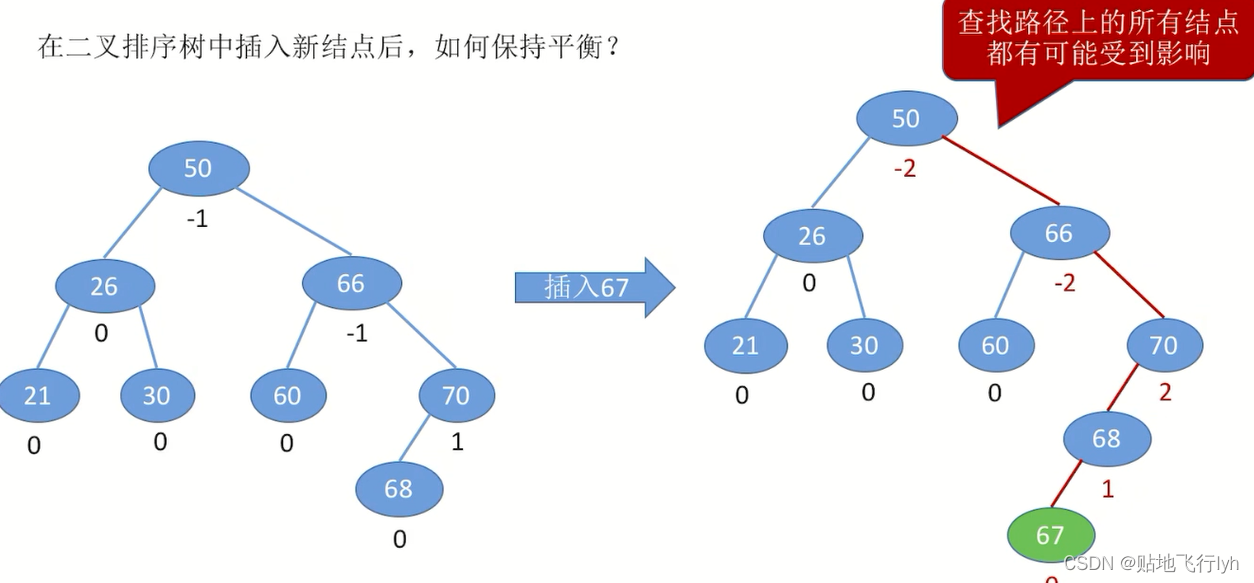
每次调整的对象都是“最小不平衡子树”,即从插入点往回找到第一个不平衡结点,调整以该结点为根的子树。下面看一个实例:
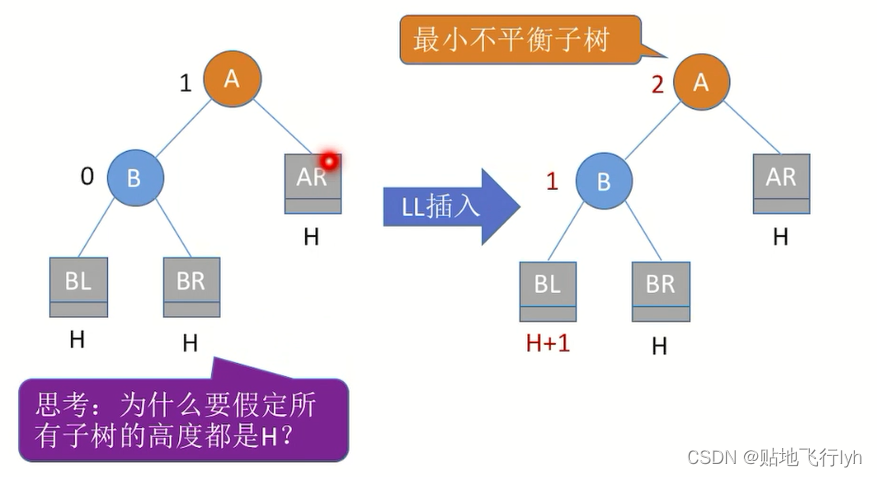
只有假设BL 、BR 、AR的高度都是H才可以保证在原本就平衡的基础上,插入数据之后A为最小不平衡字树。
调整规则:二叉排序树的特性:左子树结点值<根结点值<右子树结点值,即BL<B<BR<A<AR
调整过程:由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡。那么怎么再次恢复平衡呢?需要一次向右的旋转操作:将A的左孩子B向右上旋转代替A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。调整之后如下图:
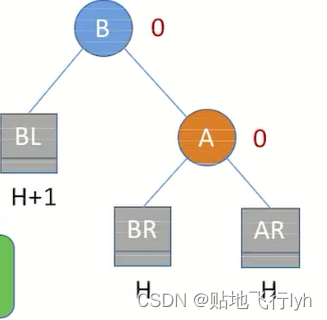
除此之外还有RR型、 LR型、 RL型等,对此感兴趣的小伙伴可以自行课下探索。