递推掌握核心：

• 递推公式(规律)
• 递推边界(初始化条件)
  
  分析题目意思：如下图
  
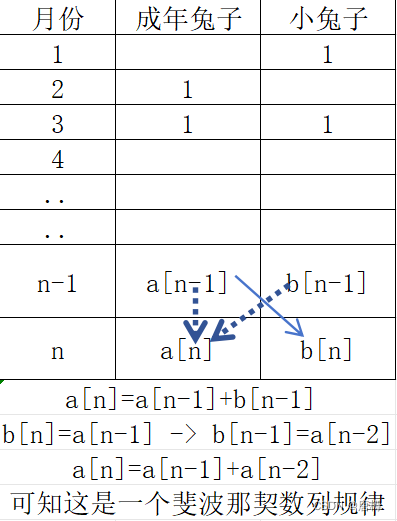
  递推式：a[n] = a[n-1]+a[n-2];
  递推边界：a[1]=1 a[2]=2

---

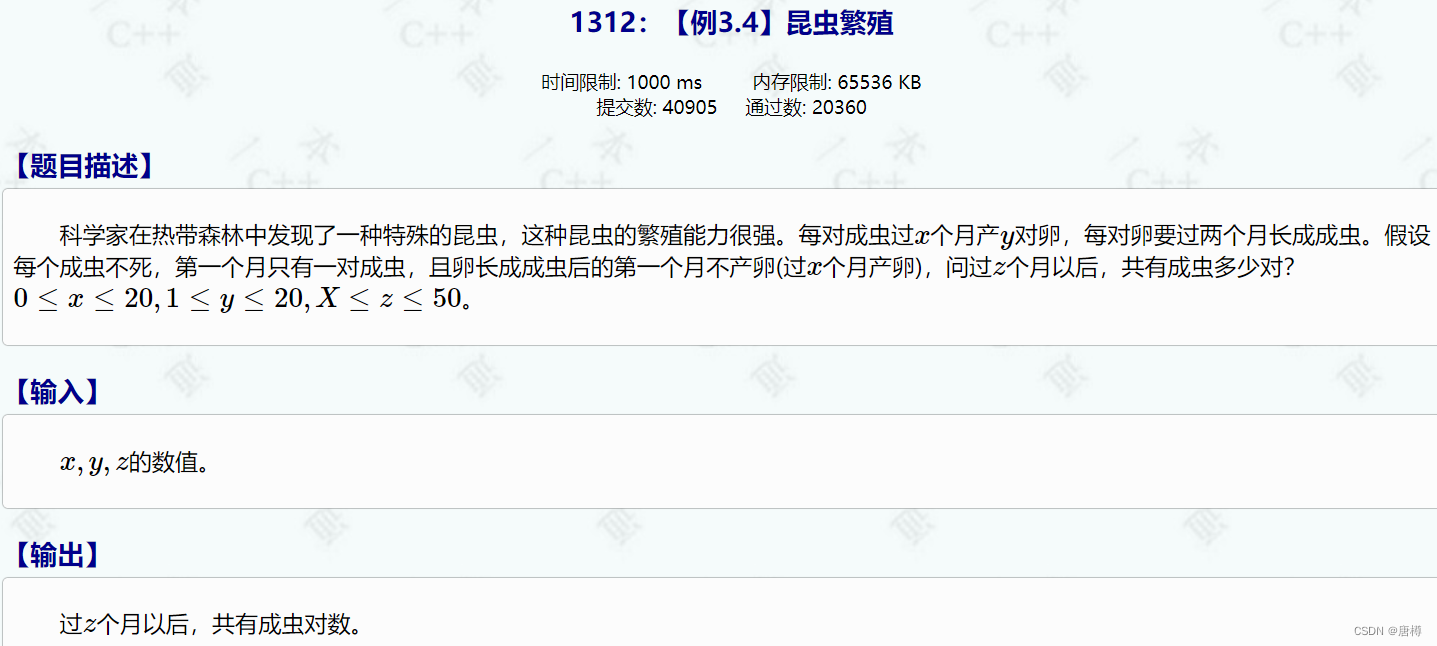
#include<iostream>
using namespace std;
long long a[100],x,y,z;
int main(){ //昆虫繁衍 
	cin>>x>>y>>z;
	//x月前面 
	for(int i=1;i<=x;i++){
		a[i]=1; //一对成虫 
	} 
	//x月后面 
	for(int i=x+1;i<=z+1;i++){
		//递推公式 a[n]=a[n-1]+a[n-x-2]*y
		a[i]=a[i-1]+a[i-x-2]*y;
	} 
	cout<<a[z+1];
	return 0;
}

题目意思：卒从A点到B点可以走哪几条路？有前提条件：卒只能往下或往右走！ 马的位置和8个控制点不能走！

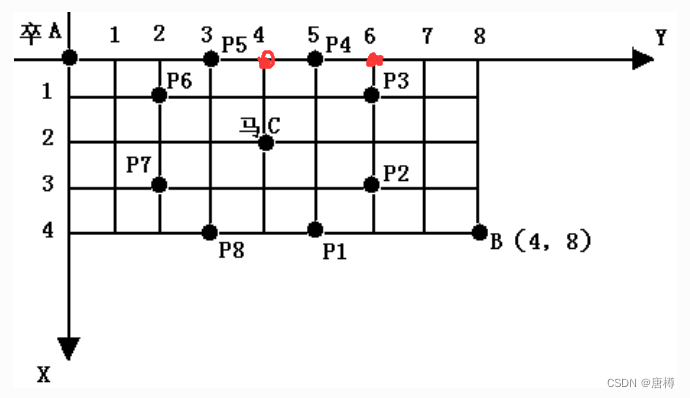
由于卒一直往右走，我们知道(0,3)这个P5点是被马控制的，不能走，那(0,4) 在P5的后面也走不了！

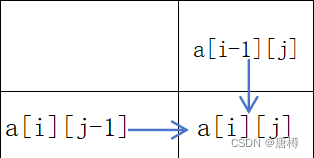
• 递推式：a[i][j]=a[i-1][j]+a[i][j-1];

#include<bits/stdc++.h>
using namespace std;
int a[30][30]; //数组存储这个坐标点的路径数 
bool flag[30][30]; //标记这个点是否能走 
int b[8][2]={{-1,-2},{1,-2},{-2,-1},{2,-1},{1,2},{-1,2},{2,1},{-2,1}};

int main(){
	int n,m,x,y;
	cin>>n>>m>>x>>y;
	flag[x][y]=true; 
	//马的坐标x,y 标记true，代表不能走 
	for(int i=0;i<8;i++){ //马的8个控制点也不能走 
		int tx = x+b[i][0]; //8个控制点的x坐标 
		int ty = y+b[i][1]; //8个控制点的y坐标 
		if(tx>=0 && tx<=n && ty>=0 && ty<=m){ //坐标满足在范围内 
			flag[tx][ty]=true; //标记true，代表不能走 
		} 
	}
	
	for(int i=0;i<=n;i++){
		for(int j=0;j<=m;j++){ //遍历整个二维数组 
			if(flag[i][j]==true){
				a[i][j]=0; //这个点的路径为0 
			}
		    else if (i==0 && j==0){
				a[i][j]=1; //地点位置路径数为1 
			}
			else if(i==0 && j!=0){
				//单行(0,1) (0,2)的路径数由前面的位置决定！
				a[i][j] = a[i][j-1];
			}
			else if(j==0 && i!=0){
				//单列(1,0) (2,0)的路径数由前面的位置决定！
				a[i][j] = a[i-1][j];
			}
			else{ //递推规律 
				a[i][j]=a[i-1][j]+a[i][j-1];
			}
		}
	}
	cout<<a[n][m];
	return 0;
}

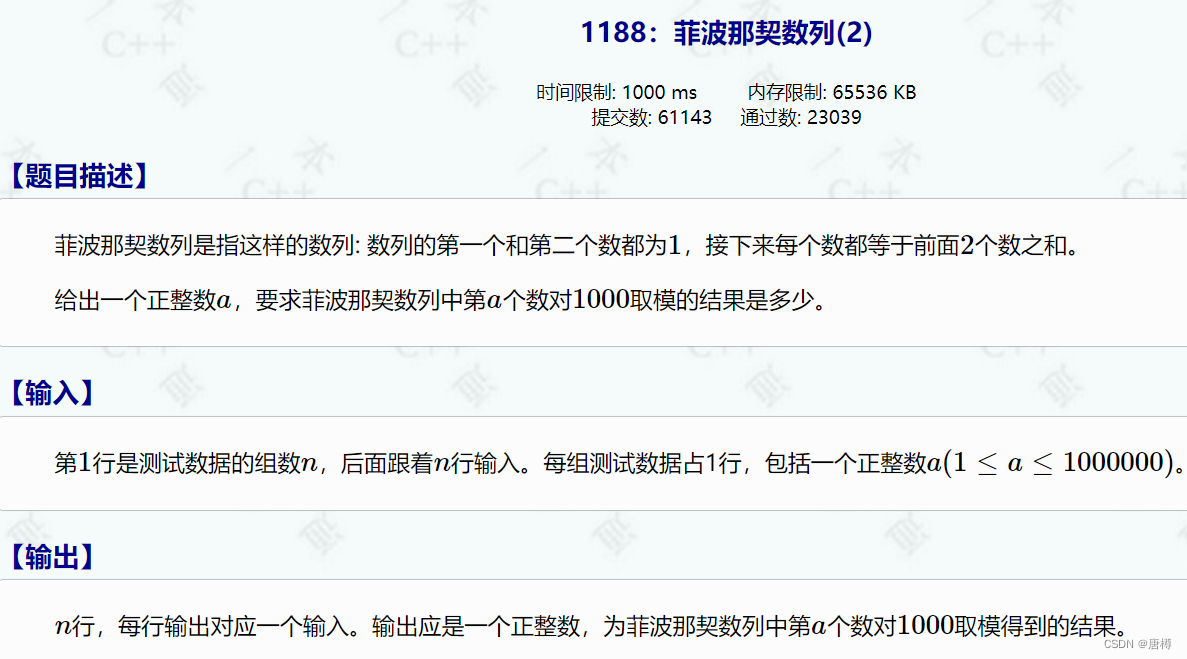
这道题比较简单，需要注意 对第a个数取模1000。 在递推式的时候就要实现，不然在输出那里因为运算的结果太大会报错！！！
递推式：f[i] = (f[i-1]+f[i-2])%1000;

#include<bits/stdc++.h>
using namespace std;
long long f[1000002]; 
int main(){
	f[1]=f[2]=1;
	int n,a;
	cin>>n;
	for(int i=3;i<=1000000;i++){ //斐波那契数列1-100000的值 
		f[i] = (f[i-1]+f[i-2])%1000; //递推式 
	}
	for(int i=1;i<=n;i++){ 
	//根据题目条件，n行，每一行有第a个数列，输出第a个斐波那契数列值 
		cin>>a;
		cout<<f[a]<<endl;
	}
	return 0;
}

这题也不难，只要知道递推式，递推边界即可！

很明显递推式：f[i] = (2*f[i-1]+f[i-2])%32767

#include<bits/stdc++.h>
using namespace std;
long long f[1000009]; 
int main(){
	f[1]=1;
	f[2]=2;
	int n,a;
	for(int i=3;i<=1000000;i++){
		f[i] = (2*f[i-1]+f[i-2])%32767;
	}
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a;
		cout<<f[a]<<endl;
	}
	return 0;
}

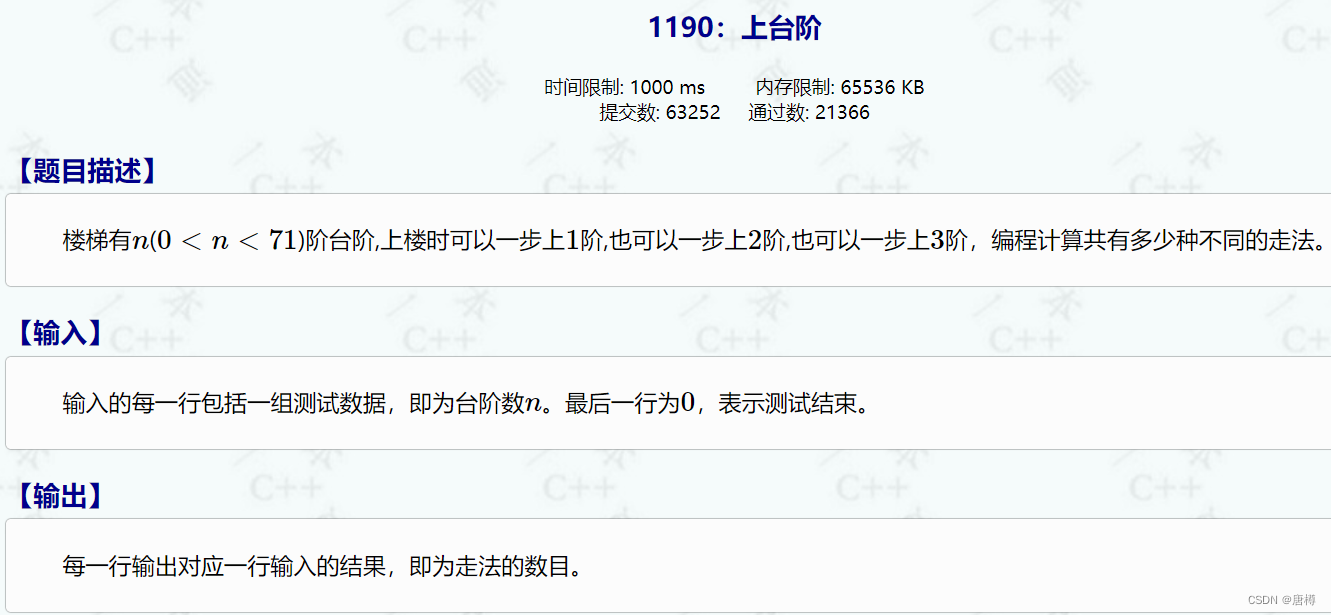
上台阶也是一种斐波那契数列。
递推式：a[i] = a[i-1]+a[i-2]+a[i-3];
递推边界：a[1]=1; a[2]=2; a[3]=4;

#include<iostream>
using namespace std;
long long a[100];
int main(){
	a[1]=1;
	a[2]=2;
	a[3]=4;
	int n;
	do{
		cin>>n;
		if(n==1 || n==2 || n==3){
			cout<<a[n]<<endl;
		}
		else{
			for(int i=4;i<=n;i++){
				a[i] = a[i-1]+a[i-2]+a[i-3];
			}
			if(n==0){
				return 0; 
			}
			cout<<a[n]<<endl;
		}
	}while(n!=0);
	return 0;
}

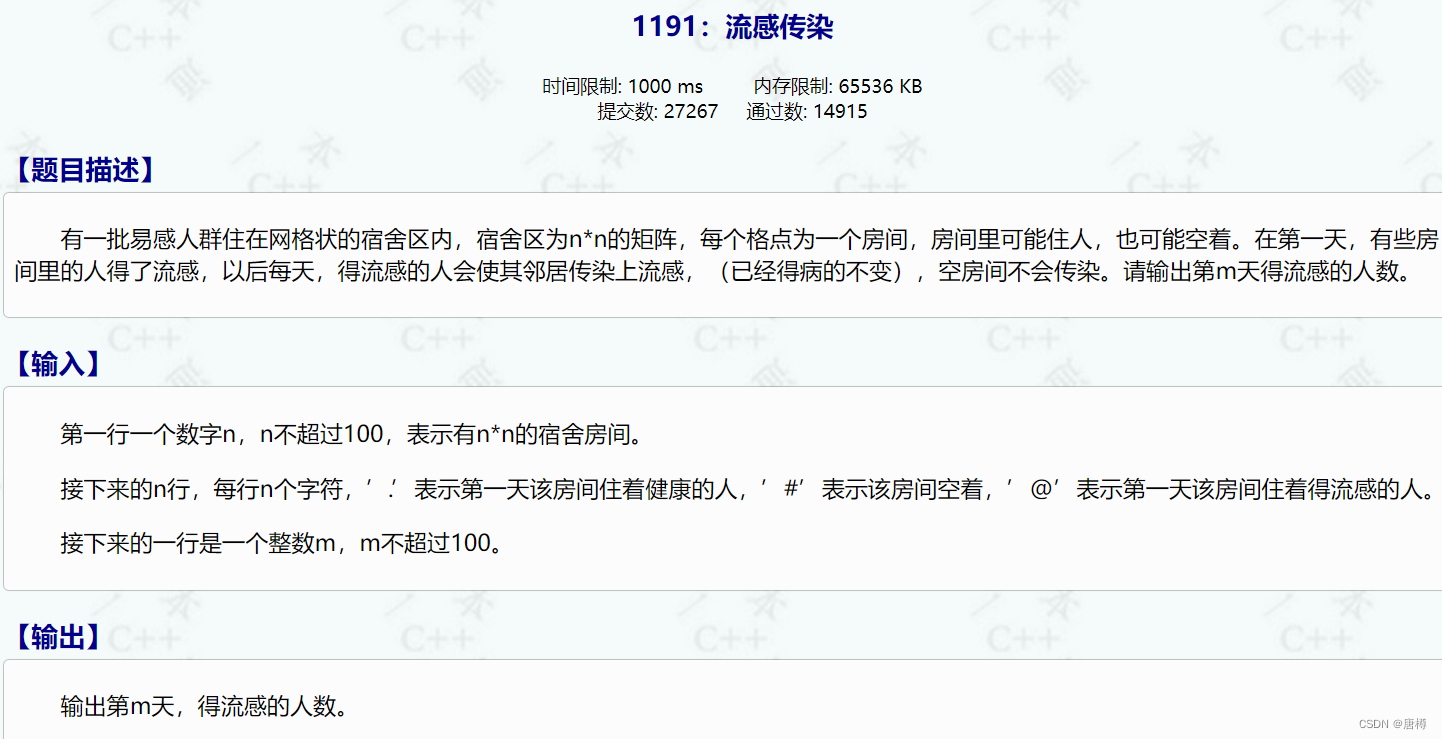
1.输入二维数组 n*n 值；
2.如果某房间坐标有感染，那这个人房间位置的上下左右都要标记感染，额外判断空房间不感染；
3.遍历一遍房间如果是被标记感染的，则把房间健康的人变成感染！
4.m天次，就是重复执行 步骤2 3；
5.最后统计第m天的感染人数，并输出

//1191：流感传染
#include<bits/stdc++.h>
using namespace std;
char a[105][105];
bool flag[105][105]={0};
int main(){
	int n,m,cnt=0;
	cin>>n;
	for(int i=1;i<=n;i++){ //输入第一天值 
		for(int j=1;j<=n;j++){
			cin>>a[i][j];
		}
	}
	cin>>m;
	for(int k=2;k<=m;k++){// 第2天到第m天 
		for(int i=1;i<=n;i++){ //遍历一遍房间 
			for(int j=1;j<=n;j++){
				if(a[i][j]=='@'){ //房间的人是感染则
					//上下左右有人的房间标记感染 
					if(a[i-1][j]=='.') flag[i-1][j]=true;
					if(a[i+1][j]=='.') flag[i+1][j]=true;
					if(a[i][j-1]=='.') flag[i][j-1]=true;
					if(a[i][j+1]=='.') flag[i][j+1]=true;
				}
			}
		}
		for(int i=1;i<=n;i++){ 
		//再遍历一遍房间， 
			for(int j=1;j<=n;j++){
				if(flag[i][j]==true){ // 对感染的房间里的人改变状态，
					a[i][j]='@'; //标记生病 
				}
			}
		}
	}
	//第m天后，统计感染的的人数，并输出 
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(a[i][j]=='@'){
				cnt++;
			}
		}
	}
	cout<<cnt;
	return 0;
}

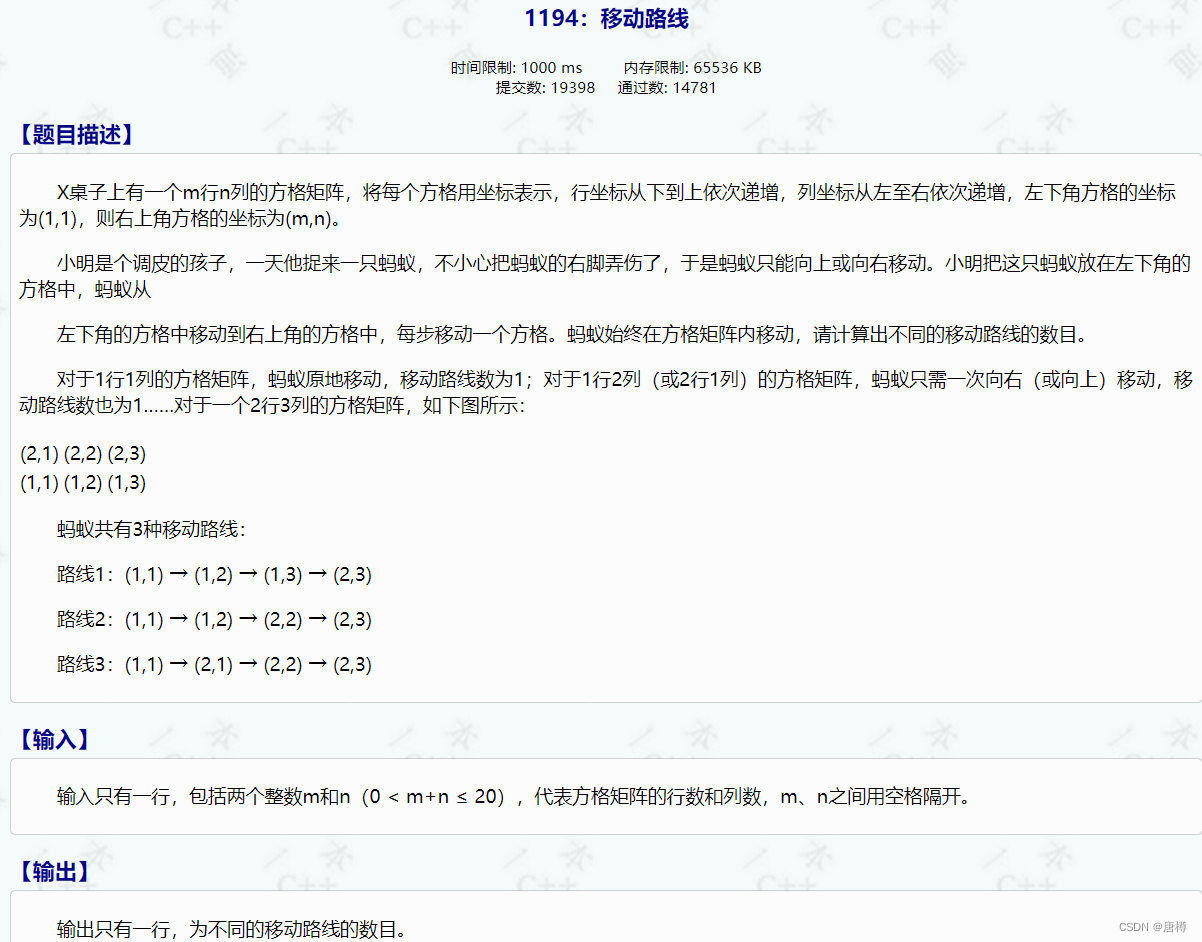
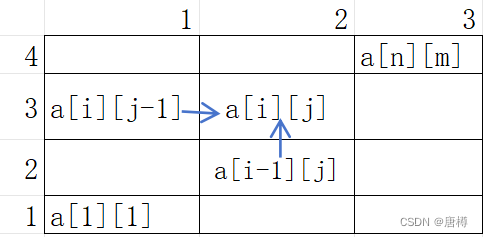
这道题跟“过河卒”很像，而且简单些。前提条件：只能往上或往右走！ ，也就是行会变大、或列变大。 计算走的路线和。 注意单行单列只有一种走法！

• 递推式：a[i][j]=a[i-1][j] + a[i][j-1];

#include<bits/stdc++.h>
using namespace std;
int a[21][21];
int main(){
	int m,n;
	cin>>m>>n;
	for(int i=1;i<=m;i++){
		for(int j=1;j<=n;j++){
			if(i==1 && j!=1){ //单行(1,1) (1,2)的路径数1
				a[1][j]=1;
			}
			else if(j==1 && i!=1){ //单列(1,1) (2,1)的路径数1
				a[i][1]=1;
			}
			else{ //往上走或往右走的递推公式 
				a[i][j]=a[i-1][j] + a[i][j-1];
			}
		}
	}
	cout<<a[m][n];
	return 0;
}