NNDL 实验八网络优化与正则化（3）不同优化算法比较

文章目录

- 7.3 不同优化算法的比较分析
- - 7.3.1 优化算法的实验设定
  - - 7.3.1.1 2D可视化实验
    - 7.3.1.2 简单拟合实验
    - 7.3.1.3 与Torch API对比，验证正确性
  - 7.3.2 学习率调整
  - - 7.3.2.1 AdaGrad算法
    - 7.3.2.2 RMSprop算法
  - 7.3.3 梯度估计修正
  - - 7.3.3.1 动量法
    - 7.3.3.2 Adam算法
  - 7.3.4 不同优化器的3D可视化对比
- 【选做题】
- 总结

7.3 不同优化算法的比较分析

除了批大小对模型收敛速度的影响外，学习率和梯度估计也是影响神经网络优化的重要因素。

神经网络优化中常用的优化方法也主要是如下两方面的改进，包括：

学习率调整：通过自适应地调整学习率使得优化更稳定。AdaGrad、RMSprop、AdaDelta算法等。
梯度估计修正：通过修正每次迭代时估计的梯度方向来加快收敛速度。动量法、Nesterov加速梯度方法等。
本节还会介绍综合学习率调整和梯度估计修正的优化算法，如Adam算法。

7.3.1 优化算法的实验设定

7.3.1.1 2D可视化实验

为了更好地展示不同优化算法的能力对比，我们选择一个二维空间中的凸函数，然后用不同的优化算法来寻找最优解，并可视化梯度下降过程的轨迹。
在这里插入图片描述
将被优化函数实现为OptimizedFunction算子，其forward方法是Sphere函数的前向计算，backward方法则计算被优化函数对x的偏导。代码实现如下：

from nndl.op import Op
import torch
class OptimizedFunction(Op):
    def __init__(self, w):
        super(OptimizedFunction, self).__init__()
        self.w = torch.as_tensor(w,dtype=torch.float32)
        self.params = {'x': torch.as_tensor(0,dtype=torch.float32)}
        self.grads = {'x': torch.as_tensor(0,dtype=torch.float32)}

    def forward(self, x):
        self.params['x'] = x
        return torch.matmul(self.w.T, torch.square(self.params['x']))

    def backward(self):
        self.grads['x'] = 2 * torch.multiply(self.w.T, self.params['x'])

nndl.op.Op：

class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(torch.as_tensor(inputs,dtype=torch.float32))

    def forward(self, inputs):
        raise NotImplementedError

    def backward(self, inputs):
        raise NotImplementedError

小批量梯度下降优化器复用3.1.4.3节定义的梯度下降优化器SimpleBatchGD。
训练函数定义一个简易的训练函数，记录梯度下降过程中每轮的参数x和损失。代码实现如下：

def train_f(model, optimizer, x_init, epoch):
    x = x_init
    all_x = []
    losses = []
    for i in range(epoch):
        all_x.append(copy.copy(x.numpy()))
        loss = model(x)
        losses.append(loss)
        model.backward()
        optimizer.step()
        x = model.params['x']
    return torch.as_tensor(all_x), losses

可视化函数定义一个Visualization类，用于绘制x的更新轨迹。代码实现如下：

import numpy as np
import matplotlib.pyplot as plt
class Visualization(object):
    def __init__(self):
        x1 = np.arange(-5, 5, 0.1)
        x2 = np.arange(-5, 5, 0.1)
        x1, x2 = np.meshgrid(x1, x2)
        self.init_x = torch.as_tensor([x1, x2])

    def plot_2d(self, model, x, fig_name):
        fig, ax = plt.subplots(figsize=(10, 6))
        cp = ax.contourf(self.init_x[0], self.init_x[1], model(self.init_x.transpose(1,0)), colors=['#e4007f', '#f19ec2', '#e86096', '#eb7aaa', '#f6c8dc', '#f5f5f5', '#000000'])
        c = ax.contour(self.init_x[0], self.init_x[1], model(self.init_x.transpose(1,0)), colors='black')
        cbar = fig.colorbar(cp)
        ax.plot(x[:, 0], x[:, 1], '-o', color='#000000')
        ax.plot(0, 'r*', markersize=18, color='#fefefe')

        ax.set_xlabel('$x1$')
        ax.set_ylabel('$x2$')

        ax.set_xlim((-2, 5))
        ax.set_ylim((-2, 5))
        plt.savefig(fig_name)

定义train_and_plot_f函数，调用train_f和Visualization，训练模型并可视化参数更新轨迹。代码实现如下：

def train_and_plot_f(model, optimizer, epoch, fig_name):
    x_init = torch.as_tensor([3, 4], dtype=torch.float32)
    print('x1 initiate: {}, x2 initiate: {}'.format(x_init[0].numpy(), x_init[1].numpy()))
    x, losses = train_f(model, optimizer, x_init, epoch)
    losses = np.array(losses)

    # 展示x1、x2的更新轨迹
    vis = Visualization()
    vis.plot_2d(model, x, fig_name)

模型训练与可视化:

from nndl.op import SimpleBatchGD
# 固定随机种子
torch.seed()
w = torch.as_tensor([0.2, 2])
model = OptimizedFunction(w)
opt = SimpleBatchGD(init_lr=0.2, model=model)
# train_and_plot_f(model, opt, epoch=20, fig_name='opti-vis-para.pdf')

nndl.op.SimpleBatchGD：

class SimpleBatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        #参数更新
        if isinstance(self.model.params, dict):
            for key in self.model.params.keys():
                self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]

Optimizer：

# 优化器基类
class Optimizer(object):
    def __init__(self, init_lr, model):
        self.init_lr = init_lr
        #指定优化器需要优化的模型
        self.model = model

    @abstractmethod
    def step(self):
        pass

结果：
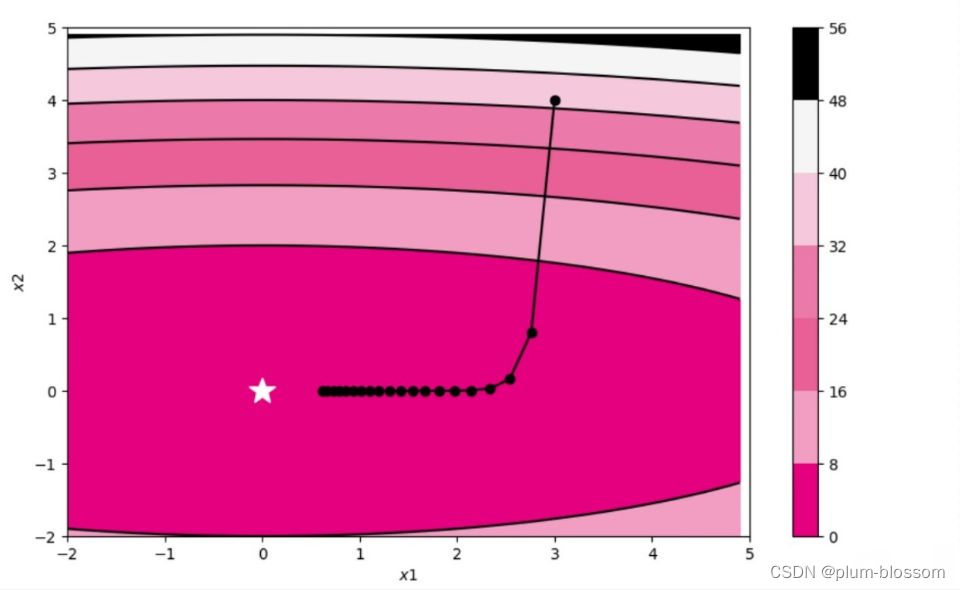
在这里插入图片描述
输出图中不同颜色代表f(x1,x2)的值，具体数值可以参考图右侧的对应表，比如深粉色区域代表f(x1,x2)在0～8之间，不同颜色间黑色的曲线是等值线，代表落在该线上的点对应的f(x1,x2)的值都相同。

7.3.1.2 简单拟合实验

这里我们随机生成一组数据作为数据样本，再构建一个简单的单层前馈神经网络，用于前向计算。

与Paddle API对比，验证正确性

分别实例化自定义SimpleBatchGD优化器和调用paddle.optimizer.SGD API, 验证自定义优化器的正确性。

# 固定随机种子
torch.seed()
# 随机生成shape为（1000，2）的训练数据
X = torch.randn([1000, 2])
w = torch.as_tensor([0.5, 0.8])
w = torch.unsqueeze(w, dim=1)
noise = 0.01 * torch.rand([1000])
noise = torch.unsqueeze(noise, dim=1)
# 计算y
y = torch.matmul(X, w) + noise
# 打印X, y样本
print('X: ', X[0].numpy())
print('y: ', y[0].numpy())

# X，y组成训练样本数据
data = torch.concat((X, y), dim=1)
print('input data shape: ', data.shape)
print('data: ', data[0].numpy())

运行结果：
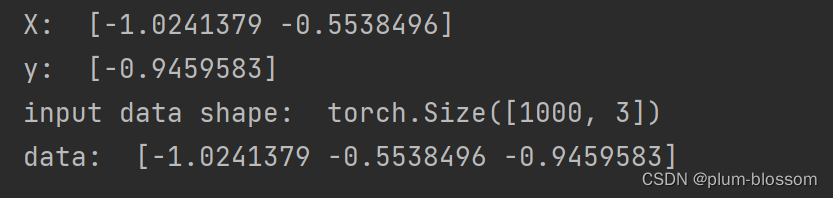
在这里插入图片描述
定义Linear算子，实现一个线性层的前向和反向计算。代码实现如下：

class Linear(Op):
    def __init__(self, input_size,  weight_init=np.random.standard_normal, bias_init=torch.zeros):
        self.params = {}
        self.params['W'] = weight_init([input_size, 1])
        self.params['W'] = torch.as_tensor(self.params['W'],dtype=torch.float32)
        self.params['b'] = bias_init([1])

        self.inputs = None
        self.grads = {}

    def forward(self, inputs):
        self.inputs = inputs
        self.outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return self.outputs

    def backward(self, labels):
        K = self.inputs.shape[0]
        self.grads['W'] = 1./ K*torch.matmul(self.inputs.T, (self.outputs - labels))
        self.grads['b'] = 1./K* torch.sum(self.outputs-labels, dim=0)

模型训练train函数的代码实现如下：

def train(data, num_epochs, batch_size, model, calculate_loss, optimizer, verbose=False):

    # 记录每个回合损失的变化
    epoch_loss = []
    # 记录每次迭代损失的变化
    iter_loss = []
    N = len(data)
    for epoch_id in range(num_epochs):
        # np.random.shuffle(data) #不再随机打乱数据
        # 将训练数据进行拆分，每个mini_batch包含batch_size条的数据
        mini_batches = [data[i:i+batch_size] for i in range(0, N, batch_size)]
        for iter_id, mini_batch in enumerate(mini_batches):
            # data中前两个分量为X
            inputs = mini_batch[:, :-1]
            # data中最后一个分量为y
            labels = mini_batch[:, -1:]
            # 前向计算
            outputs = model(inputs)
            # 计算损失
            loss = calculate_loss(outputs, labels).numpy()
            # 计算梯度
            model.backward(labels)
            # 梯度更新
            optimizer.step()
            iter_loss.append(loss)
        # verbose = True 则打印当前回合的损失
        if verbose:
            print('Epoch {:3d}, loss = {:.4f}'.format(epoch_id, np.mean(iter_loss)))
        epoch_loss.append(np.mean(iter_loss))
    return iter_loss, epoch_loss

优化过程可视化定义plot_loss函数，用于绘制损失函数变化趋势。代码实现如下：

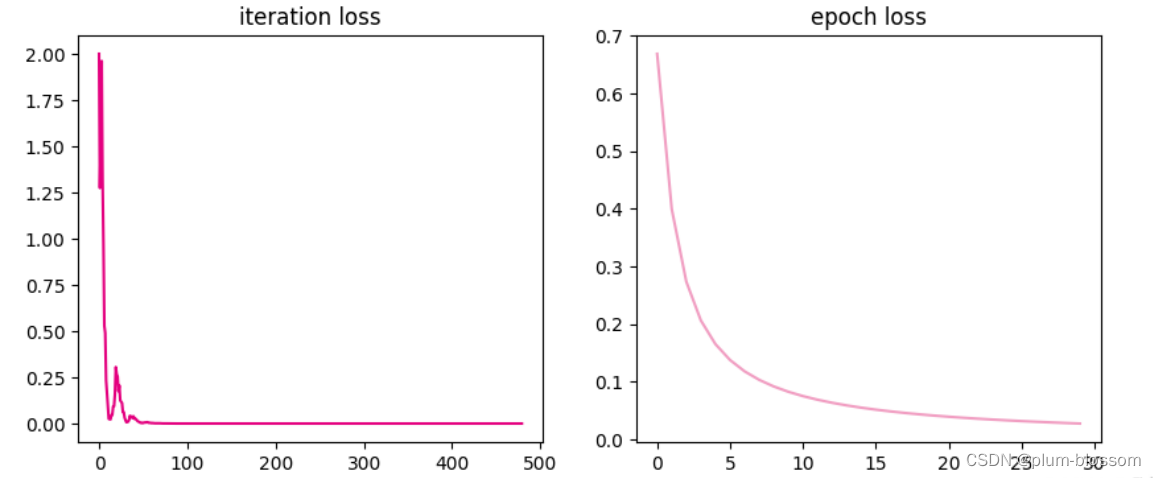
def plot_loss(iter_loss, epoch_loss, fig_name):
    """
    可视化损失函数的变化趋势
    """
    plt.figure(figsize=(10, 4))
    ax1 = plt.subplot(121)
    ax1.plot(iter_loss, color='#e4007f')
    plt.title('iteration loss')
    ax2 = plt.subplot(122)
    ax2.plot(epoch_loss, color='#f19ec2')
    plt.title('epoch loss')
    plt.savefig(fig_name)
    plt.show()

对于使用不同优化器的模型训练，保存每一个回合损失的更新情况，并绘制出损失函数的变化趋势，以此验证模型是否收敛。定义train_and_plot函数，调用train和plot_loss函数，训练并展示每个回合和每次迭代(Iteration)的损失变化情况。在模型训练时，使用torch.nn.MSELoss()计算均方误差。代码实现如下：

import torch.nn as nn
def train_and_plot(optimizer, fig_name):
    """
    训练网络并画出损失函数的变化趋势
    输入：
        - optimizer：优化器
    """
    # 定义均方差损失
    mse = nn.MSELoss()
    iter_loss, epoch_loss = train(data, num_epochs=30, batch_size=64, model=model, calculate_loss=mse, optimizer=optimizer)
    plot_loss(iter_loss, epoch_loss, fig_name)

训练网络并可视化损失函数的变化趋势。代码实现如下：

# 固定随机种子
torch.seed()
# 定义网络结构
model = Linear(2)
# 定义优化器
opt = SimpleBatchGD(init_lr=0.01, model=model)
train_and_plot(opt, 'opti-loss.pdf')

运行结果：
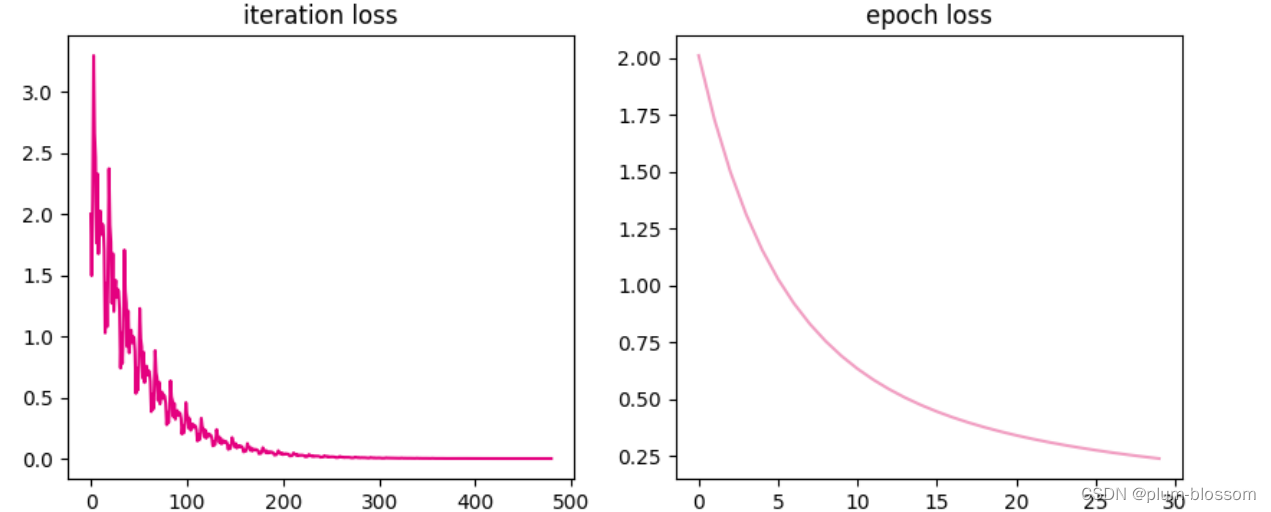
在这里插入图片描述
从输出结果可以看出：loss在不断减小，模型也在逐渐收敛。

7.3.1.3 与Torch API对比，验证正确性

分别实例化自定义SimpleBatchGD优化器和调用torch.optim.SGD API, 验证自定义优化器的正确性。代码如下：

# 固定随机种子
torch.seed()
# 定义网络结构
model = Linear(2)
# 定义优化器
opt = SimpleBatchGD(init_lr=0.01, model=model)

x = data[0, :-1].unsqueeze(0)
y = data[0, -1].unsqueeze(0)

model1 = Linear(2)
print('model1 parameter W: ', model1.params['W'].numpy())
opt1 = SimpleBatchGD(init_lr=0.01, model=model1)
output1 = model1(x)

model2 = nn.Linear(2, 1)
model2.weight = torch.nn.Parameter(model1.params['W'])
print('model2 parameter W: ', model2.state_dict()['weight'].numpy())
output2 = model2(x.T)

model1.backward(y)
opt1.step()
print('model1 parameter W after train step: ', model1.params['W'].numpy())

opt2 = torch.optim.SGD(lr=0.01, params=model2.parameters())
loss = torch.nn.functional.mse_loss(output2, y) / 2
loss.backward()
opt2.step()
opt2.zero_grad()
print('model2 parameter W after train step: ', model2.state_dict()['weight'].numpy())

运行结果：

model1 parameter W: [[ 0.8403961]
[-0.1934289]]
model2 parameter W: [[ 0.8403961 -0.1934289]]
model1 parameter W after train step: [[ 0.85348997 ]
[-0.18250407]]
model2 parameter W after train step: [[ 0.85317418 -0.1826655]]

7.3.2 学习率调整

学习率是神经网络优化时的重要超参数。在梯度下降法中，学习率α的取值非常关键，如果取值过大就不会收敛，如果过小则收敛速度太慢。
常用的学习率调整方法包括如下几种方法：

学习率衰减：如分段常数衰减（Piecewise Constant Decay）、余弦衰减（Cosine Decay）等；
学习率预热：如逐渐预热(Gradual Warmup) 等；
周期性学习率调整：如循环学习率等；
自适应调整学习率的方法：如AdaGrad、RMSprop、AdaDelta等。自适应学习率方法可以针对每个参数设置不同的学习率。

7.3.2.1 AdaGrad算法

构建优化器定义Adagrad类，继承Optimizer类。定义step函数调用adagrad进行参数更新。代码实现如下：


class Adagrad(Optimizer):
    def __init__(self, init_lr, model, epsilon):
        super(Adagrad, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.epsilon = epsilon

    def adagrad(self, x, gradient_x, G, init_lr):
        G += gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G

    def step(self):
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)

2D可视化实验使用被优化函数展示Adagrad算法的参数更新轨迹。代码实现如下：

# 固定随机种子
torch.seed()
w = torch.as_tensor([0.2, 2])
model2 = OptimizedFunction(w)
opt2 = Adagrad(init_lr=0.5, model=model2, epsilon=1e-7)
train_and_plot_f(model2, opt2, epoch=50, fig_name='opti-vis-para2.pdf')

运行结果：
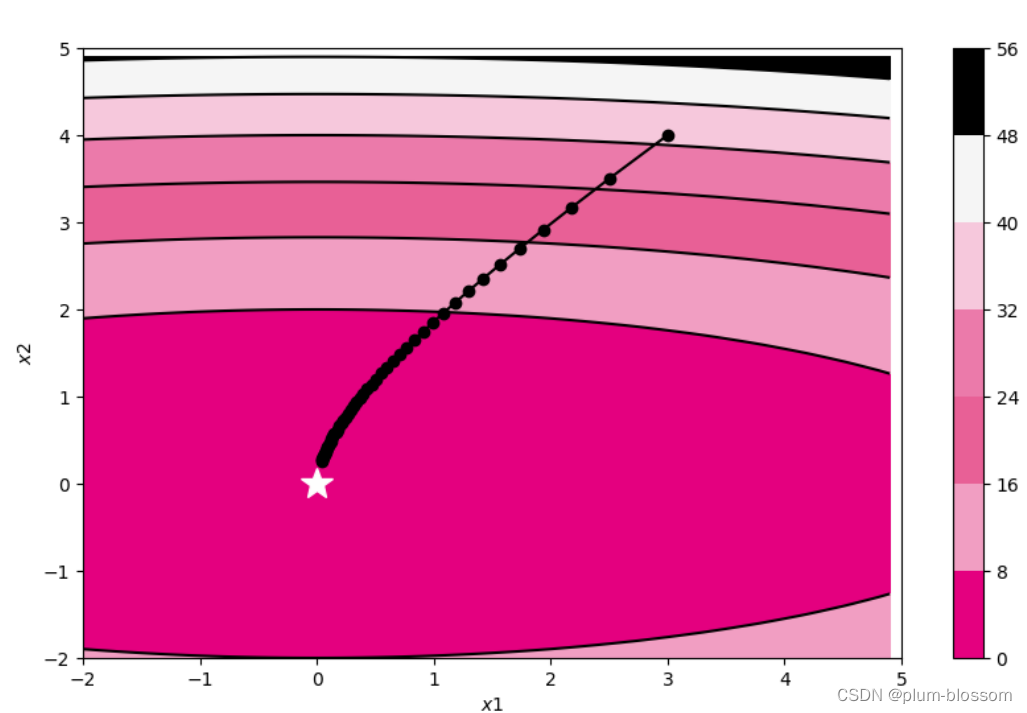
在这里插入图片描述
从输出结果看，AdaGrad算法在前几个回合更新时参数更新幅度较大，随着回合数增加，学习率逐渐缩小，参数更新幅度逐渐缩小。在AdaGrad算法中，如果某个参数的偏导数累积比较大，其学习率相对较小。相反，如果其偏导数累积较小，其学习率相对较大。但整体随着迭代次数的增加，学习率逐渐缩小。该算法的缺点是在经过一定次数的迭代依然没有找到最优点时，由于这时的学习率已经非常小，很难再继续找到最优点。

简单拟合实验训练单层线性网络，验证损失是否收敛。代码实现如下：

# 固定随机种子
torch.seed()
# 定义网络结构
model = Linear(2)
# 定义优化器
opt = Adagrad(init_lr=0.1, model=model, epsilon=1e-7)
train_and_plot(opt, 'opti-loss2.pdf')

运行结果：
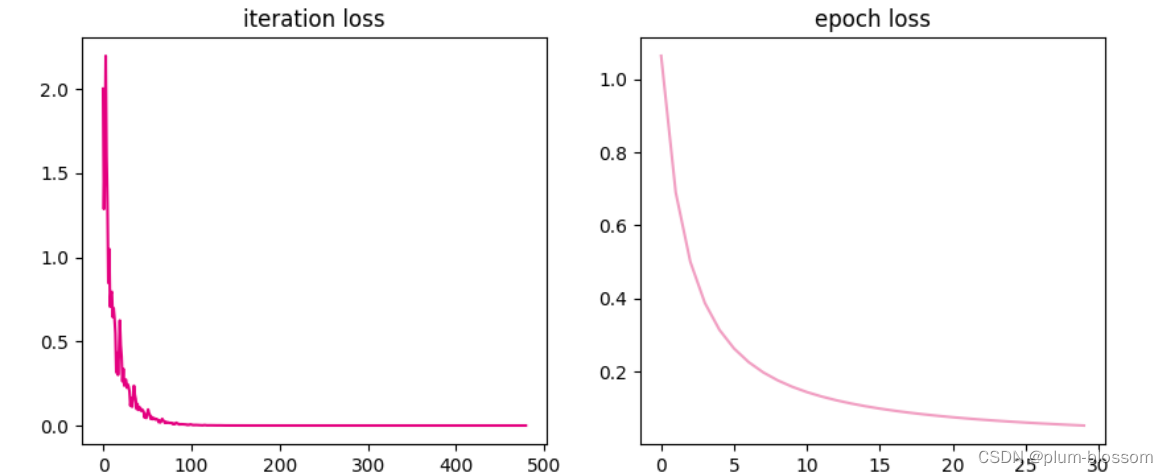
在这里插入图片描述

7.3.2.2 RMSprop算法

构建优化器定义RMSprop类，继承Optimizer类。定义step函数调用rmsprop更新参数。代码实现如下：

class RMSprop(Optimizer):
    def __init__(self, init_lr, model, beta, epsilon):
        """
        RMSprop优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - beta：衰减率
            - epsilon：保持数值稳定性而设置的常数
        """
        super(RMSprop, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.beta = beta
        self.epsilon = epsilon
 
    def rmsprop(self, x, gradient_x, G, init_lr):
        """
        rmsprop算法更新参数，G为迭代梯度平方的加权移动平均
        """
        G = self.beta * G + (1 - self.beta) * gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)

2D可视化实验使用被优化函数展示RMSprop算法的参数更新轨迹。代码实现如下：

# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = RMSprop(init_lr=0.1, model=model, beta=0.9, epsilon=1e-7)
train_and_plot_f(model, opt, epoch=50, fig_name='opti-vis-para3.pdf')

运行结果：
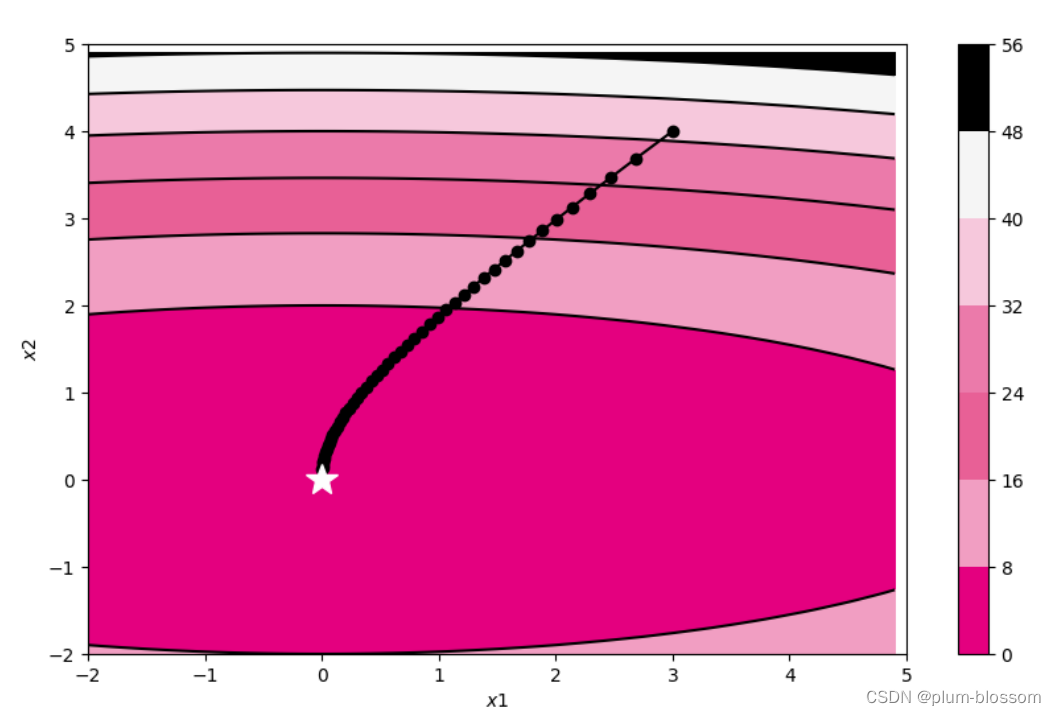
在这里插入图片描述
简单拟合实验训练单层线性网络，进行简单的拟合实验。代码实现如下：

# 固定随机种子
torch.manual_seed(0)
# 定义网络结构
model = Linear(2)
# 定义优化器
opt = RMSprop(init_lr=0.1, model=model, beta=0.9, epsilon=1e-7)
train_and_plot(opt, 'opti-loss3.pdf')

运行结果：
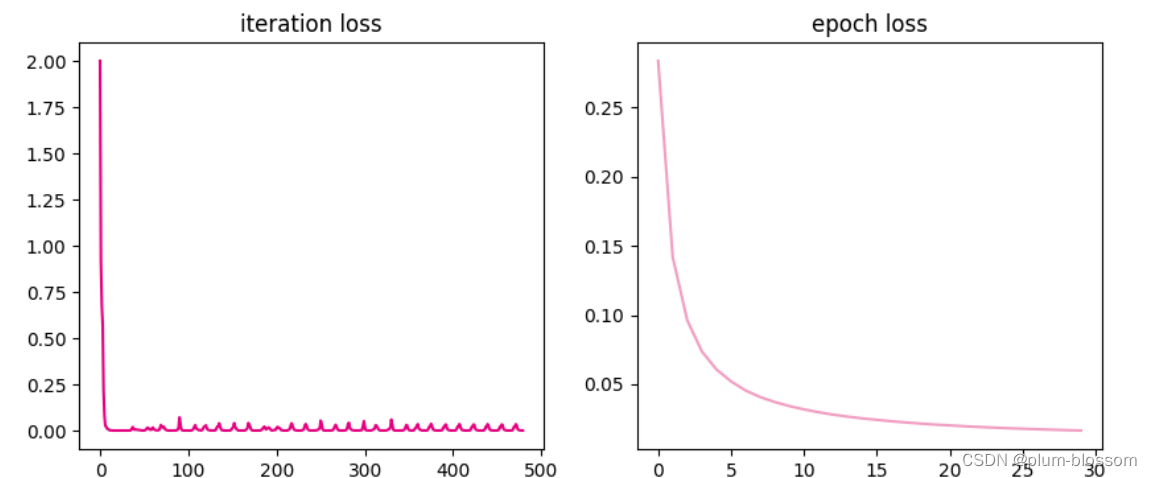
在这里插入图片描述

7.3.3 梯度估计修正

除了调整学习率之外，还可以进行梯度估计修正。在小批量梯度下降法中，由于每次迭代的样本具有一定的随机性，因此每次迭代的梯度估计和整个训练集上的最优梯度并不一致。如果每次选取样本数量比较小，损失会呈振荡的方式下降。
一种有效地缓解梯度估计随机性的方式是通过使用最近一段时间内的平均梯度来代替当前时刻的随机梯度来作为参数更新的方向，从而提高优化速度。

7.3.3.1 动量法

用之前积累动量来替代真正的梯度。每次迭代的梯度可以看作加速度。

class Momentum(Optimizer):
    def __init__(self, init_lr, model, rho):
        """
        Momentum优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - rho：动量因子
        """
        super(Momentum, self).__init__(init_lr=init_lr, model=model)
        self.delta_x = {}
        for key in self.model.params.keys():
            self.delta_x[key] = 0
        self.rho = rho
 
    def momentum(self, x, gradient_x, delta_x, init_lr):
        """
        momentum算法更新参数，delta_x为梯度的加权移动平均
        """
        delta_x = self.rho * delta_x - init_lr * gradient_x
        x += delta_x
        return x, delta_x
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],
                                                                      self.model.grads[key],
                                                                      self.delta_x[key],
                                                                      self.init_lr)

# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = Momentum(init_lr=0.01, model=model, rho=0.9)
train_and_plot_f(model, opt, epoch=50, fig_name='opti-vis-para4.pdf')

运行结果：
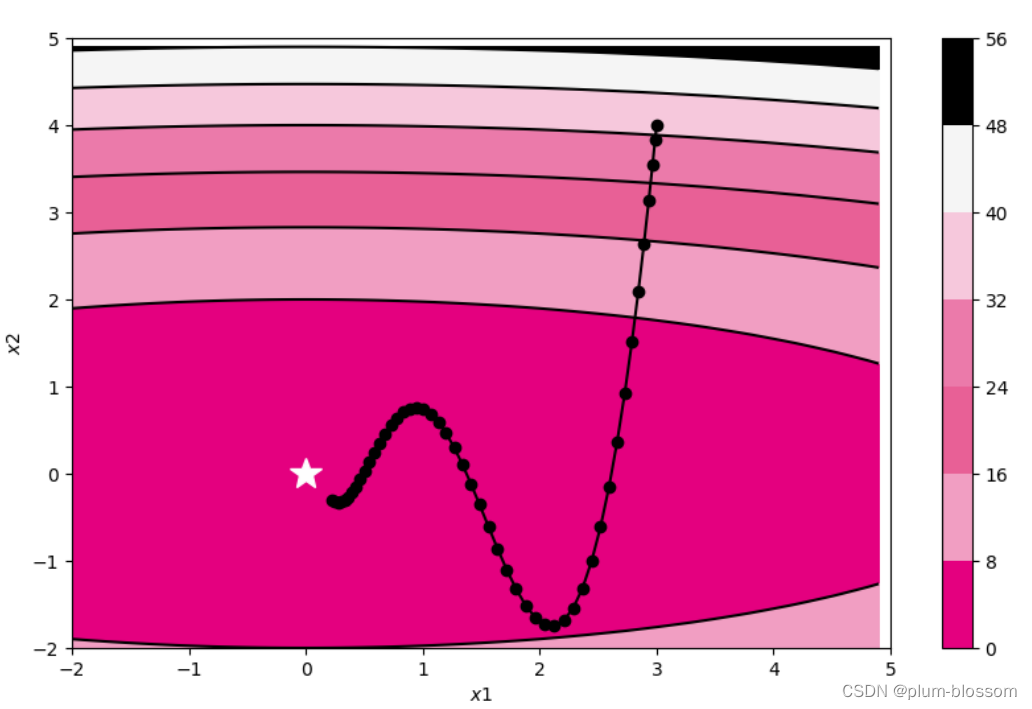
在这里插入图片描述
从输出结果可以看出:在模型训练初期，梯度方向比较一致，参数更新幅度逐渐增大;在迭代后期，参数更新幅度减小，在收敛值附近振荡。

简单拟合实验训练单层线性网络，进行简单的拟合实验。代码实现如下

# 固定随机种子
torch.manual_seed(0)
 
# 定义网络结构
model = Linear(2)
# 定义优化器
opt = Momentum(init_lr=0.01, model=model, rho=0.9)
train_and_plot(opt, 'opti-loss4.pdf')

运行结果：
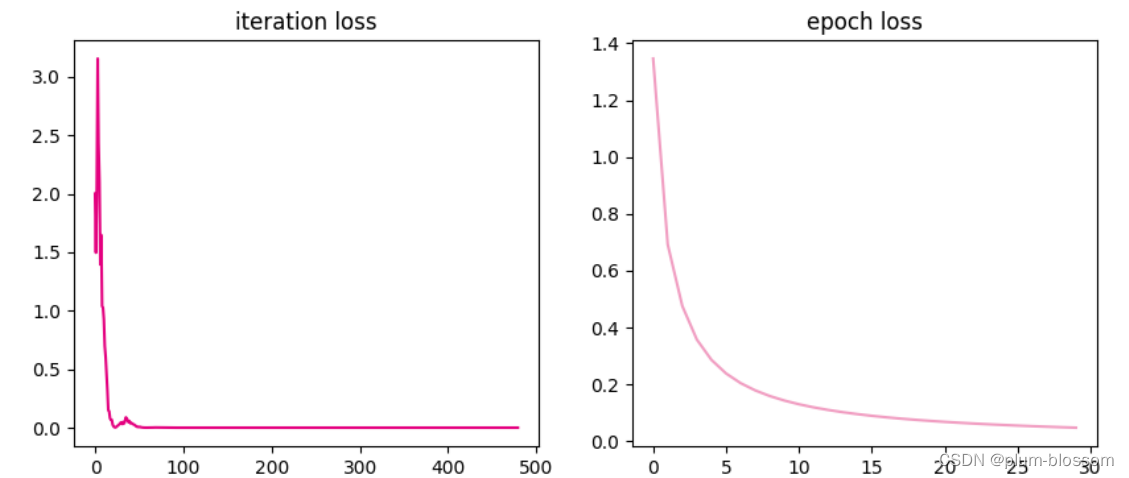
在这里插入图片描述

7.3.3.2 Adam算法

Adam算法（自适应矩估计算法）可以看作动量法和RMSprop算法的结合，不但使用动量作为参数更新方向，而且可以自适应调整学习率。

class Adam(Optimizer):
    def __init__(self, init_lr, model, beta1, beta2, epsilon):
        """
        Adam优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - beta1, beta2：移动平均的衰减率
            - epsilon：保持数值稳定性而设置的常数
        """
        super(Adam, self).__init__(init_lr=init_lr, model=model)
        self.beta1 = beta1
        self.beta2 = beta2
        self.epsilon = epsilon
        self.M, self.G = {}, {}
        for key in self.model.params.keys():
            self.M[key] = 0
            self.G[key] = 0
        self.t = 1
 
    def adam(self, x, gradient_x, G, M, t, init_lr):
        """
        adam算法更新参数
        输入：
            - x：参数
            - G：梯度平方的加权移动平均
            - M：梯度的加权移动平均
            - t：迭代次数
            - init_lr：初始学习率
        """
        M = self.beta1 * M + (1 - self.beta1) * gradient_x
        G = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2
        M_hat = M / (1 - self.beta1 ** t)
        G_hat = G / (1 - self.beta2 ** t)
        t += 1
        x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hat
        return x, G, M, t
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],
                                                                                 self.model.grads[key],
                                                                                 self.G[key],
                                                                                 self.M[key],
                                                                                 self.t,
                                                                                 self.init_lr)

# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = Adam(init_lr=0.2, model=model, beta1=0.9, beta2=0.99, epsilon=1e-7)
train_and_plot_f(model, opt, epoch=20, fig_name='opti-vis-para5.pdf')

运行结果：
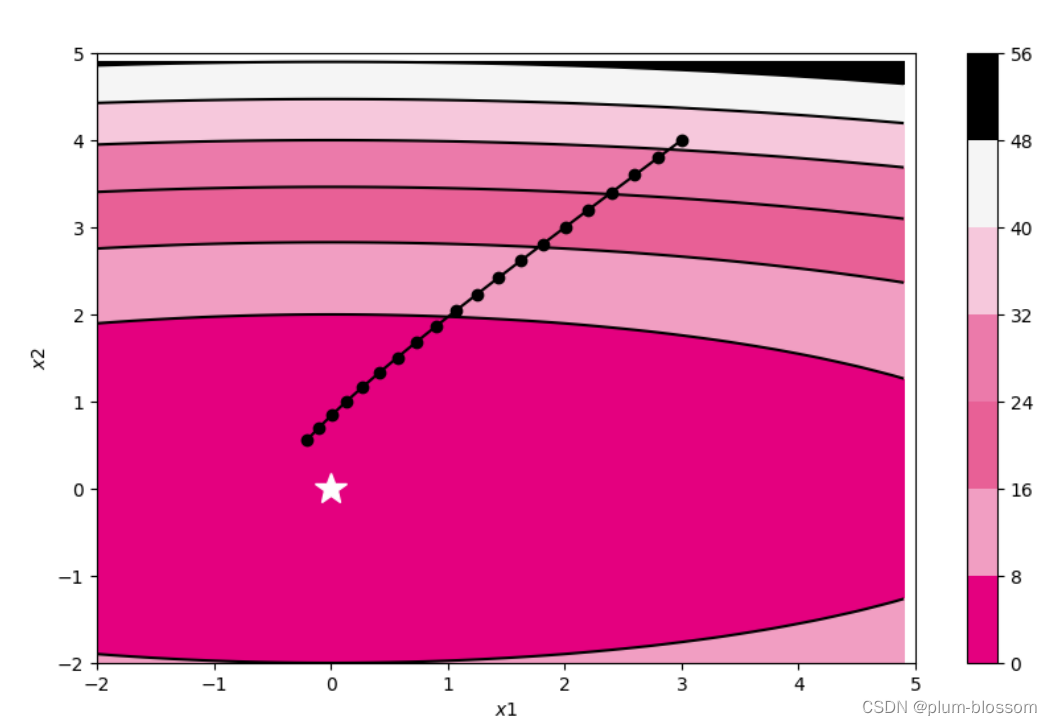
在这里插入图片描述
从输出结果看，Adam算法可以自适应调整学习率，参数更新更加平稳。
简单拟合实验训练单层线性网络，进行简单的拟合实验。代码实现如下：

# 固定随机种子
torch.manual_seed(0)
# 定义网络结构
model = Linear(2)
# 定义优化器
opt = Adam(init_lr=0.1, model=model, beta1=0.9, beta2=0.99, epsilon=1e-7)
train_and_plot(opt, 'opti-loss5.pdf')

运行结果：
在这里插入图片描述

7.3.4 不同优化器的3D可视化对比

import torch
import numpy as np
import copy
from matplotlib import pyplot as plt
from matplotlib import animation
from itertools import zip_longest
 
 
class Op(object):
    def __init__(self):
        pass
 
    def __call__(self, inputs):
        return self.forward(inputs)
 
    # 输入：张量inputs
    # 输出：张量outputs
    def forward(self, inputs):
        # return outputs
        raise NotImplementedError
 
    # 输入：最终输出对outputs的梯度outputs_grads
    # 输出：最终输出对inputs的梯度inputs_grads
    def backward(self, outputs_grads):
        # return inputs_grads
        raise NotImplementedError
 
 
class Optimizer(object):  # 优化器基类
    def __init__(self, init_lr, model):
        """
        优化器类初始化
        """
        # 初始化学习率，用于参数更新的计算
        self.init_lr = init_lr
        # 指定优化器需要优化的模型
        self.model = model
 
    def step(self):
        """
        定义每次迭代如何更新参数
        """
        pass
 
 
class SimpleBatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)
 
    def step(self):
        # 参数更新
        if isinstance(self.model.params, dict):
            for key in self.model.params.keys():
                self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]
 
 
class Adagrad(Optimizer):
    def __init__(self, init_lr, model, epsilon):
        """
        Adagrad 优化器初始化
        输入：
            - init_lr： 初始学习率 - model：模型，model.params存储模型参数值  - epsilon：保持数值稳定性而设置的非常小的常数
        """
        super(Adagrad, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.epsilon = epsilon
 
    def adagrad(self, x, gradient_x, G, init_lr):
        """
        adagrad算法更新参数，G为参数梯度平方的累计值。
        """
        G += gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G
 
    def step(self):
        """
        参数更新
        """
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)
 
 
class RMSprop(Optimizer):
    def __init__(self, init_lr, model, beta, epsilon):
        """
        RMSprop优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - beta：衰减率
            - epsilon：保持数值稳定性而设置的常数
        """
        super(RMSprop, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.beta = beta
        self.epsilon = epsilon
 
    def rmsprop(self, x, gradient_x, G, init_lr):
        """
        rmsprop算法更新参数，G为迭代梯度平方的加权移动平均
        """
        G = self.beta * G + (1 - self.beta) * gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)
 
 
class Momentum(Optimizer):
    def __init__(self, init_lr, model, rho):
        """
        Momentum优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - rho：动量因子
        """
        super(Momentum, self).__init__(init_lr=init_lr, model=model)
        self.delta_x = {}
        for key in self.model.params.keys():
            self.delta_x[key] = 0
        self.rho = rho
 
    def momentum(self, x, gradient_x, delta_x, init_lr):
        """
        momentum算法更新参数，delta_x为梯度的加权移动平均
        """
        delta_x = self.rho * delta_x - init_lr * gradient_x
        x += delta_x
        return x, delta_x
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],
                                                                      self.model.grads[key],
                                                                      self.delta_x[key],
                                                                      self.init_lr)
 
 
class Adam(Optimizer):
    def __init__(self, init_lr, model, beta1, beta2, epsilon):
        """
        Adam优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - beta1, beta2：移动平均的衰减率
            - epsilon：保持数值稳定性而设置的常数
        """
        super(Adam, self).__init__(init_lr=init_lr, model=model)
        self.beta1 = beta1
        self.beta2 = beta2
        self.epsilon = epsilon
        self.M, self.G = {}, {}
        for key in self.model.params.keys():
            self.M[key] = 0
            self.G[key] = 0
        self.t = 1
 
    def adam(self, x, gradient_x, G, M, t, init_lr):
        """
        adam算法更新参数
        输入：
            - x：参数
            - G：梯度平方的加权移动平均
            - M：梯度的加权移动平均
            - t：迭代次数
            - init_lr：初始学习率
        """
        M = self.beta1 * M + (1 - self.beta1) * gradient_x
        G = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2
        M_hat = M / (1 - self.beta1 ** t)
        G_hat = G / (1 - self.beta2 ** t)
        t += 1
        x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hat
        return x, G, M, t
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],
                                                                                 self.model.grads[key],
                                                                                 self.G[key],
                                                                                 self.M[key],
                                                                                 self.t,
                                                                                 self.init_lr)
 
 
class OptimizedFunction3D(Op):
    def __init__(self):
        super(OptimizedFunction3D, self).__init__()
        self.params = {'x': 0}
        self.grads = {'x': 0}
 
    def forward(self, x):
        self.params['x'] = x
        return x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]
 
    def backward(self):
        x = self.params['x']
        gradient1 = 2 * x[0] + x[1]
        gradient2 = 2 * x[1] + 3 * x[1] ** 2 + x[0]
        grad1 = torch.Tensor([gradient1])
        grad2 = torch.Tensor([gradient2])
        self.grads['x'] = torch.cat([grad1, grad2])
 
 
class Visualization3D(animation.FuncAnimation):
    """    绘制动态图像，可视化参数更新轨迹    """
 
    def __init__(self, *xy_values, z_values, labels=[], colors=[], fig, ax, interval=600, blit=True, **kwargs):
        """
        初始化3d可视化类
        输入：
            xy_values：三维中x,y维度的值
            z_values：三维中z维度的值
            labels：每个参数更新轨迹的标签
            colors：每个轨迹的颜色
            interval：帧之间的延迟（以毫秒为单位）
            blit：是否优化绘图
        """
        self.fig = fig
        self.ax = ax
        self.xy_values = xy_values
        self.z_values = z_values
 
        frames = max(xy_value.shape[0] for xy_value in xy_values)
        self.lines = [ax.plot([], [], [], label=label, color=color, lw=2)[0]
                      for _, label, color in zip_longest(xy_values, labels, colors)]
        super(Visualization3D, self).__init__(fig, self.animate, init_func=self.init_animation, frames=frames,
                                              interval=interval, blit=blit, **kwargs)
 
    def init_animation(self):
        # 数值初始化
        for line in self.lines:
            line.set_data([], [])
            # line.set_3d_properties(np.asarray([]))  # 源程序中有这一行，加上会报错。 Edit by David 2022.12.4
        return self.lines
 
    def animate(self, i):
        # 将x,y,z三个数据传入，绘制三维图像
        for line, xy_value, z_value in zip(self.lines, self.xy_values, self.z_values):
            line.set_data(xy_value[:i, 0], xy_value[:i, 1])
            line.set_3d_properties(z_value[:i])
        return self.lines
 
 
def train_f(model, optimizer, x_init, epoch):
    x = x_init
    all_x = []
    losses = []
    for i in range(epoch):
        all_x.append(copy.deepcopy(x.numpy()))  # 浅拷贝 改为 深拷贝, 否则List的原值会被改变。 Edit by David 2022.12.4.
        loss = model(x)
        losses.append(loss)
        model.backward()
        optimizer.step()
        x = model.params['x']
    return torch.Tensor(np.array(all_x)), losses
 
 
# 构建5个模型，分别配备不同的优化器
model1 = OptimizedFunction3D()
opt_gd = SimpleBatchGD(init_lr=0.01, model=model1)
 
model2 = OptimizedFunction3D()
opt_adagrad = Adagrad(init_lr=0.5, model=model2, epsilon=1e-7)
 
model3 = OptimizedFunction3D()
opt_rmsprop = RMSprop(init_lr=0.1, model=model3, beta=0.9, epsilon=1e-7)
 
model4 = OptimizedFunction3D()
opt_momentum = Momentum(init_lr=0.01, model=model4, rho=0.9)
 
model5 = OptimizedFunction3D()
opt_adam = Adam(init_lr=0.1, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)
 
models = [model1, model2, model3, model4, model5]
opts = [opt_gd, opt_adagrad, opt_rmsprop, opt_momentum, opt_adam]
 
x_all_opts = []
z_all_opts = []
 
# 使用不同优化器训练
 
for model, opt in zip(models, opts):
    x_init = torch.FloatTensor([2, 3])
    x_one_opt, z_one_opt = train_f(model, opt, x_init, 150)  # epoch
    # 保存参数值
    x_all_opts.append(x_one_opt.numpy())
    z_all_opts.append(np.squeeze(z_one_opt))
 
# 使用numpy.meshgrid生成x1,x2矩阵，矩阵的每一行为[-3, 3]，以0.1为间隔的数值
x1 = np.arange(-3, 3, 0.1)
x2 = np.arange(-3, 3, 0.1)
x1, x2 = np.meshgrid(x1, x2)
init_x = torch.Tensor(np.array([x1, x2]))
 
model = OptimizedFunction3D()
 
# 绘制 f_3d函数 的 三维图像
fig = plt.figure()
ax = plt.axes(projection='3d')
X = init_x[0].numpy()
Y = init_x[1].numpy()
Z = model(init_x).numpy()  # 改为 model(init_x).numpy() David 2022.12.4
ax.plot_surface(X, Y, Z, cmap='rainbow')
 
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x1,x2)')
 
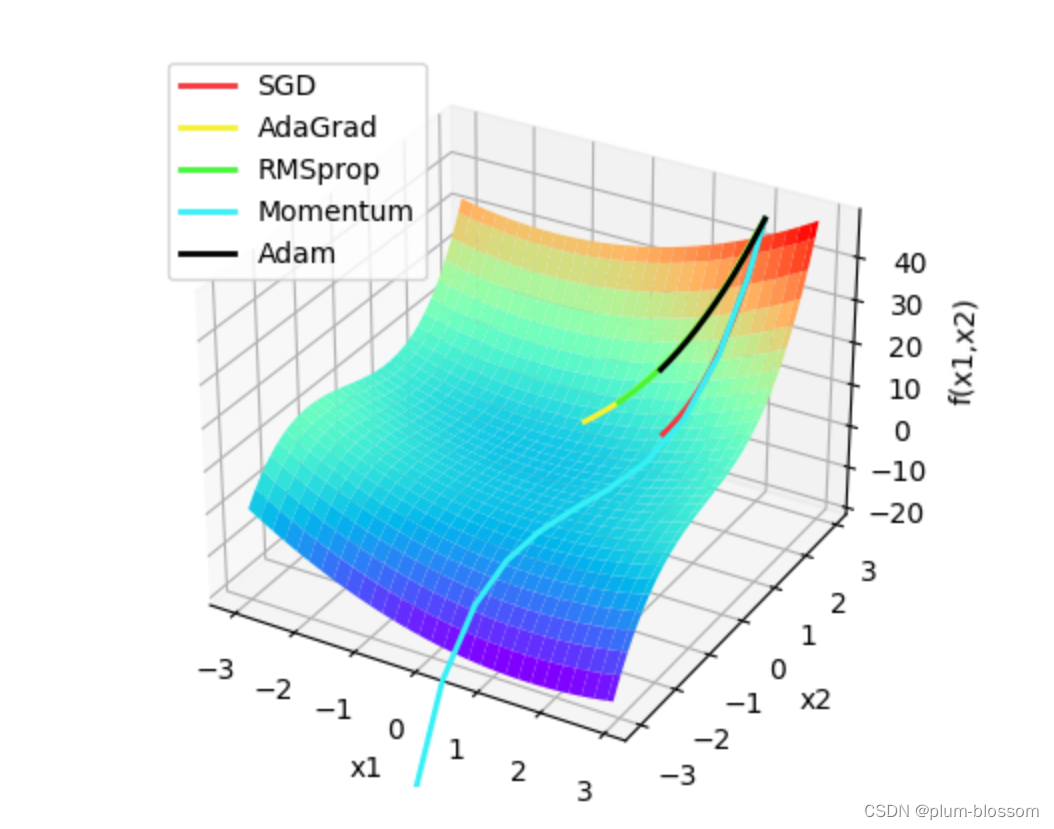
labels = ['SGD', 'AdaGrad', 'RMSprop', 'Momentum', 'Adam']
colors = ['#f6373c', '#f6f237', '#45f637', '#37f0f6', '#000000']
 
animator = Visualization3D(*x_all_opts, z_values=z_all_opts, labels=labels, colors=colors, fig=fig, ax=ax)
ax.legend(loc='upper left')
 
plt.show()
animator.save('animation.gif')

运行结果：
在这里插入图片描述

【选做题】

1.编程实现下面的动画

在这里插入图片描述
代码如下：

import torch
import numpy as np
import copy
from matplotlib import pyplot as plt
from matplotlib import animation
from itertools import zip_longest
from matplotlib import cm
 
 
class Op(object):
    def __init__(self):
        pass
 
    def __call__(self, inputs):
        return self.forward(inputs)
 
    # 输入：张量inputs
    # 输出：张量outputs
    def forward(self, inputs):
        # return outputs
        raise NotImplementedError
 
    # 输入：最终输出对outputs的梯度outputs_grads
    # 输出：最终输出对inputs的梯度inputs_grads
    def backward(self, outputs_grads):
        # return inputs_grads
        raise NotImplementedError
 
 
class Optimizer(object):  # 优化器基类
    def __init__(self, init_lr, model):
        """
        优化器类初始化
        """
        # 初始化学习率，用于参数更新的计算
        self.init_lr = init_lr
        # 指定优化器需要优化的模型
        self.model = model
 
    def step(self):
        """
        定义每次迭代如何更新参数
        """
        pass
 
 
class SimpleBatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)
 
    def step(self):
        # 参数更新
        if isinstance(self.model.params, dict):
            for key in self.model.params.keys():
                self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]
 
 
class Adagrad(Optimizer):
    def __init__(self, init_lr, model, epsilon):
        """
        Adagrad 优化器初始化
        输入：
            - init_lr： 初始学习率 - model：模型，model.params存储模型参数值  - epsilon：保持数值稳定性而设置的非常小的常数
        """
        super(Adagrad, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.epsilon = epsilon
 
    def adagrad(self, x, gradient_x, G, init_lr):
        """
        adagrad算法更新参数，G为参数梯度平方的累计值。
        """
        G += gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G
 
    def step(self):
        """
        参数更新
        """
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)
 
 
class RMSprop(Optimizer):
    def __init__(self, init_lr, model, beta, epsilon):
        """
        RMSprop优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - beta：衰减率
            - epsilon：保持数值稳定性而设置的常数
        """
        super(RMSprop, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.beta = beta
        self.epsilon = epsilon
 
    def rmsprop(self, x, gradient_x, G, init_lr):
        """
        rmsprop算法更新参数，G为迭代梯度平方的加权移动平均
        """
        G = self.beta * G + (1 - self.beta) * gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)
 
 
class Momentum(Optimizer):
    def __init__(self, init_lr, model, rho):
        """
        Momentum优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - rho：动量因子
        """
        super(Momentum, self).__init__(init_lr=init_lr, model=model)
        self.delta_x = {}
        for key in self.model.params.keys():
            self.delta_x[key] = 0
        self.rho = rho
 
    def momentum(self, x, gradient_x, delta_x, init_lr):
        """
        momentum算法更新参数，delta_x为梯度的加权移动平均
        """
        delta_x = self.rho * delta_x - init_lr * gradient_x
        x += delta_x
        return x, delta_x
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],
                                                                      self.model.grads[key],
                                                                      self.delta_x[key],
                                                                      self.init_lr)
 
 
class Adam(Optimizer):
    def __init__(self, init_lr, model, beta1, beta2, epsilon):
        """
        Adam优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - beta1, beta2：移动平均的衰减率
            - epsilon：保持数值稳定性而设置的常数
        """
        super(Adam, self).__init__(init_lr=init_lr, model=model)
        self.beta1 = beta1
        self.beta2 = beta2
        self.epsilon = epsilon
        self.M, self.G = {}, {}
        for key in self.model.params.keys():
            self.M[key] = 0
            self.G[key] = 0
        self.t = 1
 
    def adam(self, x, gradient_x, G, M, t, init_lr):
        """
        adam算法更新参数
        输入：
            - x：参数
            - G：梯度平方的加权移动平均
            - M：梯度的加权移动平均
            - t：迭代次数
            - init_lr：初始学习率
        """
        M = self.beta1 * M + (1 - self.beta1) * gradient_x
        G = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2
        M_hat = M / (1 - self.beta1 ** t)
        G_hat = G / (1 - self.beta2 ** t)
        t += 1
        x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hat
        return x, G, M, t
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],
                                                                                 self.model.grads[key],
                                                                                 self.G[key],
                                                                                 self.M[key],
                                                                                 self.t,
                                                                                 self.init_lr)
 
 
class OptimizedFunction3D(Op):
    def __init__(self):
        super(OptimizedFunction3D, self).__init__()
        self.params = {'x': 0}
        self.grads = {'x': 0}
 
    def forward(self, x):
        self.params['x'] = x
        return - x[0] * x[0] / 2 + x[1] * x[1] / 1  # x[0] ** 2 + x[1] ** 2 + x[1] ** 3 + x[0] * x[1]
 
    def backward(self):
        x = self.params['x']
        gradient1 = - 2 * x[0] / 2
        gradient2 = 2 * x[1] / 1
        grad1 = torch.Tensor([gradient1])
        grad2 = torch.Tensor([gradient2])
        self.grads['x'] = torch.cat([grad1, grad2])
 
 
class Visualization3D(animation.FuncAnimation):
    """    绘制动态图像，可视化参数更新轨迹    """
 
    def __init__(self, *xy_values, z_values, labels=[], colors=[], fig, ax, interval=100, blit=True, **kwargs):
        """
        初始化3d可视化类
        输入：
            xy_values：三维中x,y维度的值
            z_values：三维中z维度的值
            labels：每个参数更新轨迹的标签
            colors：每个轨迹的颜色
            interval：帧之间的延迟（以毫秒为单位）
            blit：是否优化绘图
        """
        self.fig = fig
        self.ax = ax
        self.xy_values = xy_values
        self.z_values = z_values
 
        frames = max(xy_value.shape[0] for xy_value in xy_values)
 
        self.lines = [ax.plot([], [], [], label=label, color=color, lw=2)[0]
                      for _, label, color in zip_longest(xy_values, labels, colors)]
        self.points = [ax.plot([], [], [], color=color, markeredgewidth=1, markeredgecolor='black', marker='o')[0]
                       for _, color in zip_longest(xy_values, colors)]
        # print(self.lines)
        super(Visualization3D, self).__init__(fig, self.animate, init_func=self.init_animation, frames=frames,
                                              interval=interval, blit=blit, **kwargs)
 
    def init_animation(self):
        # 数值初始化
        for line in self.lines:
            line.set_data_3d([], [], [])
        for point in self.points:
            point.set_data_3d([], [], [])
        return self.points + self.lines
 
    def animate(self, i):
        # 将x,y,z三个数据传入，绘制三维图像
        for line, xy_value, z_value in zip(self.lines, self.xy_values, self.z_values):
            line.set_data_3d(xy_value[:i, 0], xy_value[:i, 1], z_value[:i])
        for point, xy_value, z_value in zip(self.points, self.xy_values, self.z_values):
            point.set_data_3d(xy_value[i, 0], xy_value[i, 1], z_value[i])
        return self.points + self.lines
 
 
def train_f(model, optimizer, x_init, epoch):
    x = x_init
    all_x = []
    losses = []
    for i in range(epoch):
        all_x.append(copy.deepcopy(x.numpy()))  # 浅拷贝 改为 深拷贝, 否则List的原值会被改变。 Edit by David 2022.12.4.
        loss = model(x)
        losses.append(loss)
        model.backward()
        optimizer.step()
        x = model.params['x']
    return torch.Tensor(np.array(all_x)), losses
 
 
# 构建5个模型，分别配备不同的优化器
model1 = OptimizedFunction3D()
opt_gd = SimpleBatchGD(init_lr=0.05, model=model1)
 
model2 = OptimizedFunction3D()
opt_adagrad = Adagrad(init_lr=0.05, model=model2, epsilon=1e-7)
 
model3 = OptimizedFunction3D()
opt_rmsprop = RMSprop(init_lr=0.05, model=model3, beta=0.9, epsilon=1e-7)
 
model4 = OptimizedFunction3D()
opt_momentum = Momentum(init_lr=0.05, model=model4, rho=0.9)
 
model5 = OptimizedFunction3D()
opt_adam = Adam(init_lr=0.05, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)
 
models = [model5, model2, model3, model4, model1]
opts = [opt_adam, opt_adagrad, opt_rmsprop, opt_momentum, opt_gd]
 
x_all_opts = []
z_all_opts = []
 
# 使用不同优化器训练
 
for model, opt in zip(models, opts):
    x_init = torch.FloatTensor([0.00001, 0.5])
    x_one_opt, z_one_opt = train_f(model, opt, x_init, 100)  # epoch
    # 保存参数值
    x_all_opts.append(x_one_opt.numpy())
    z_all_opts.append(np.squeeze(z_one_opt))
 
# 使用numpy.meshgrid生成x1,x2矩阵，矩阵的每一行为[-3, 3]，以0.1为间隔的数值
x1 = np.arange(-1, 2, 0.01)
x2 = np.arange(-1, 1, 0.05)
x1, x2 = np.meshgrid(x1, x2)
init_x = torch.Tensor(np.array([x1, x2]))
 
model = OptimizedFunction3D()
 
# 绘制 f_3d函数 的 三维图像
fig = plt.figure()
ax = plt.axes(projection='3d')
X = init_x[0].numpy()
Y = init_x[1].numpy()
Z = model(init_x).numpy()  # 改为 model(init_x).numpy() David 2022.12.4
surf = ax.plot_surface(X, Y, Z, edgecolor='grey', cmap=cm.coolwarm)
# fig.colorbar(surf, shrink=0.5, aspect=1)
ax.set_zlim(-3, 2)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x1,x2)')
 
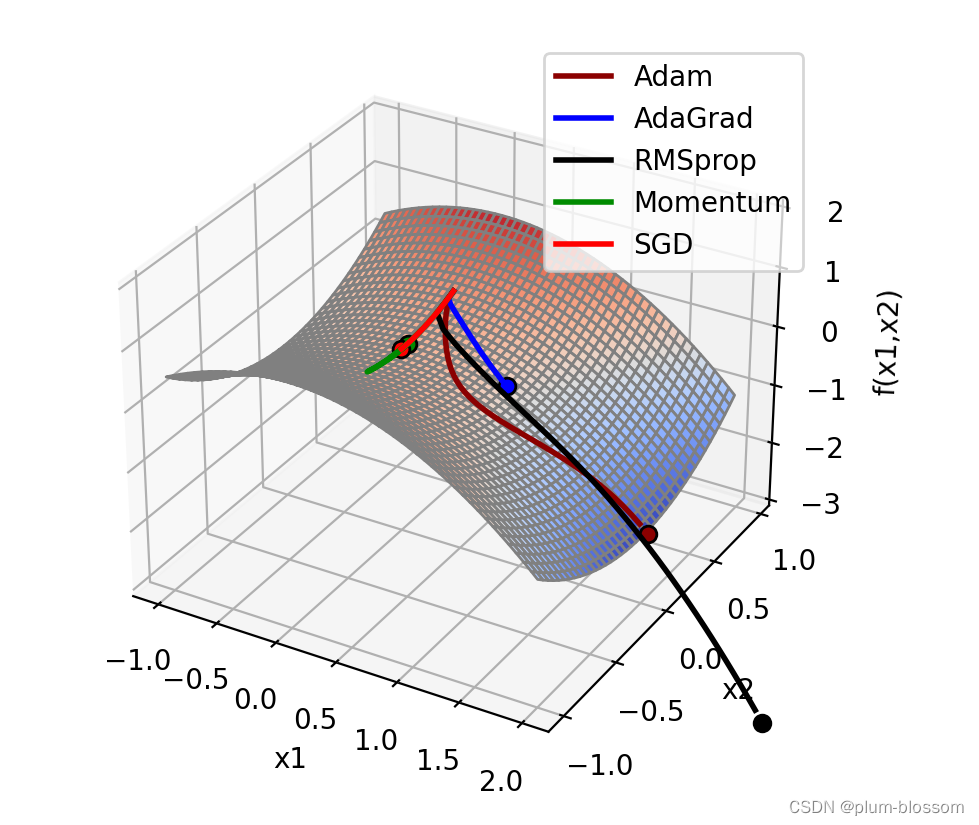
labels = ['Adam', 'AdaGrad', 'RMSprop', 'Momentum', 'SGD']
colors = ['#8B0000', '#0000FF', '#000000', '#008B00', '#FF0000']
 
animator = Visualization3D(*x_all_opts, z_values=z_all_opts, labels=labels, colors=colors, fig=fig, ax=ax)
ax.legend(loc='upper right')
 
plt.show()