题目描述：

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [width(i), length(i), height(i)]（下标从 0 开始）。请你从 cuboids 选出一个子集，并将它们堆叠起来。
如果 width(i) <= width(j) 且 length(i) <= length(j) 且 height(i) <= height(j) ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。
返回堆叠长方体 cuboids 可以得到的最大高度。

测试用例：

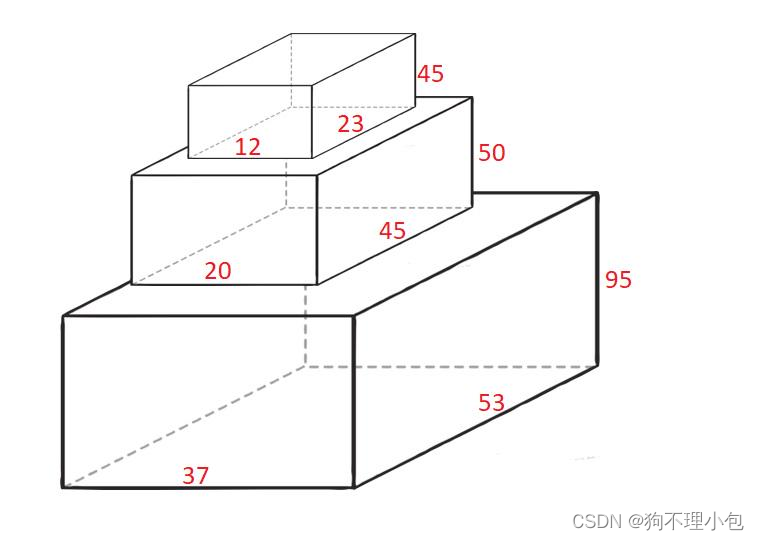
在这里插入图片描述

示例1：
输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
输出：190
解释：第 1个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。

示例 2：
输入：cuboids = [[38,25,45],[76,35,3]]
输出：76
解释：无法将任何长方体放在另一个上面。
选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。

分析：

本题允许我们旋转长方体，意味着我们可以选择长方体的任意一边作为长方体的“高”。对于任意一种合法的堆叠，如果我们把里面每个长方体都旋转至“长 <= 宽 <= 高”，堆叠仍然是合法的，并且能够保证堆叠的高度最大化。

因此，我们可以把所有长方体的边长进行排序，使得每个长方体满足“长 <= 宽 <= 高”。然后将每个长方体升序排列。
然后本题就可以转化成经典的线性dp问题最长递增子序列
来源：力扣（LeetCode）ylb:https://leetcode.cn/problems/maximum-height-by-stacking-cuboids/solutions/2014535/by-lcbin-1uv5/

代码：

func maxHeight(cuboids [][]int) (ans int) {
    for _, v := range cuboids {
        sort.Ints(v)   //对每个长方体按照长 <= 宽 <= 高排序
    }
    //将每个长方体升序排列
    sort.Slice(cuboids, func(i, j int) bool {  
        a, b := cuboids[i], cuboids[j]
        return a[0] < b[0] || a[0] == b[0] && (a[1] < b[1] || a[1] == b[1] && a[2] < b[2])
    })
    n := len(cuboids)
    f := make([]int, n)
    for i := range f { //这里dp的意思大致是将第i个长方体堆叠在之前最高长度的堆叠体上，而j就是已经堆叠的长方体
        for j := 0; j < i; j++ {
            //满足可堆叠的条件后再选出i之前最高的堆叠体
            if cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2] {
                f[i] = max(f[i], f[j])
            }
        }
        f[i] += cuboids[i][2]  //加上之前最高堆叠体高度就是第i个最高堆叠体
        ans = max(ans, f[i])   //每次循环求得最大的结果
    }
    return
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}