前言

在实际工作中，我们经常会遇到这样一类问题：给机器输入大量的特征数据，并期望机器通过学习找到数据中存在的某种共性特征或者结构，亦或是数据之间存在的某种关联。
例如，视频网站根据用户的观看行为对用户进行分组从而建立不同的推荐策略，或是寻找视频播放是否流畅与用户是否退订之间的关系等。这类问题被称作“非监督学习”问题，它并不是像监督学习那样希望预测某种输出结果。
相比于监督学习，非监督学习的输入数据没有标签信息，需要通过算法模型来挖掘数据内在的结构和模式。
非监督学习主要包含两大类学习方法：数据聚类和特征变量关联。其中，聚类算法往往是通过多次迭代来找到数据的最优分割，而特征变量关联则是利用各种相关性分析方法来找到变量之间的关系。

K均值聚类

场景描述
支持向量机、逻辑回归、决策树等经典的机器学习算法主要用于分类问题，即根据一些已给定类别的样本，训练某种分类器，使得它能够对类别未知的样本进行分类。与分类问题不同，聚类是在事先并不知道任何样本类别标签的情况下，通过数据之间的内在关系把样本划分为若干类别，使得同类别样本之间的相似度高，不同类别之间的样本相似度低。

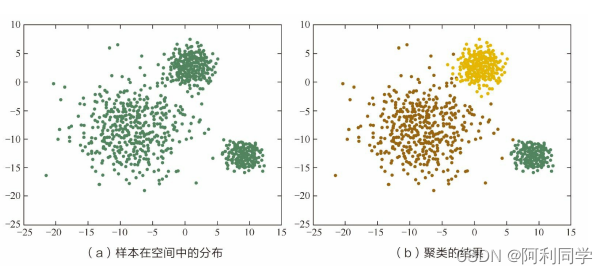
（不同颜色代表不同类别）。

分类问题属于监督学习的范畴，而聚类则是非监督学习。K均值聚类（KMeans Clustering）是最基础和最常用的聚类算法。它的基本思想是，通过迭代方式寻找K个簇（Cluster）的一种划分方案，使得聚类结果对应的代价函数最小。特别地，代价函数可以定义为各个样本距离所属簇中心点的误差平方和

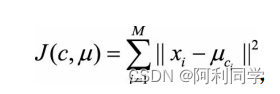
其中xi代表第i个样本，ci是xi所属于的簇，μci代表簇对应的中心点，M是样本总数。

算法描述

K均值聚类的核心目标是将给定的数据集划分成K个簇，并给出每个数据对应的簇中心点。算法的具体步骤描述如下：

流程

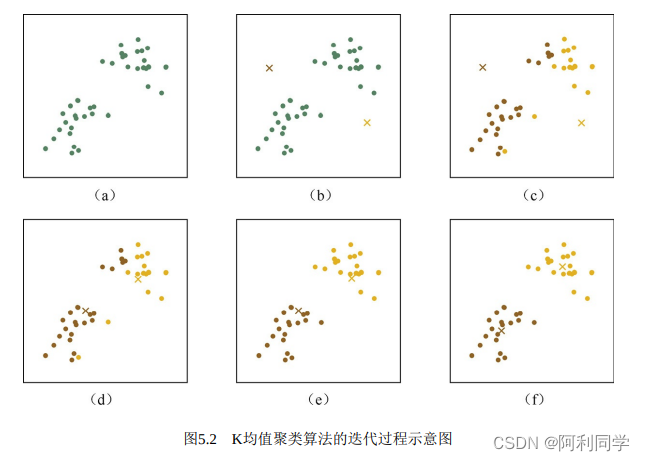
图2是K-means算法的一个迭代过程示意图。首先，给定二维空间上的一些样本点（见图2（a）），直观上这些点可以被分成两类；
接下来，初始化两个中心点（图2（b）的棕色和黄色叉子代表中心点），并根据中心点的位计算每个样本所属的簇（图2（c）用不同颜色表示）；
然后根据每个簇中的所有点的平均值计算新的中心点位置（见图2（d））；图2（e）和图2（f）展示了新一轮的迭代结果；在经过两轮的迭代之后，算法基本收敛。

优缺点

K均值算法的主要缺点如下。
（1）需要人工预先确定初始K值，且该值和真实的数据分布未必吻合。
（2）K均值只能收敛到局部最优，效果受到初始值很大。
（3）易受到噪点的影响。