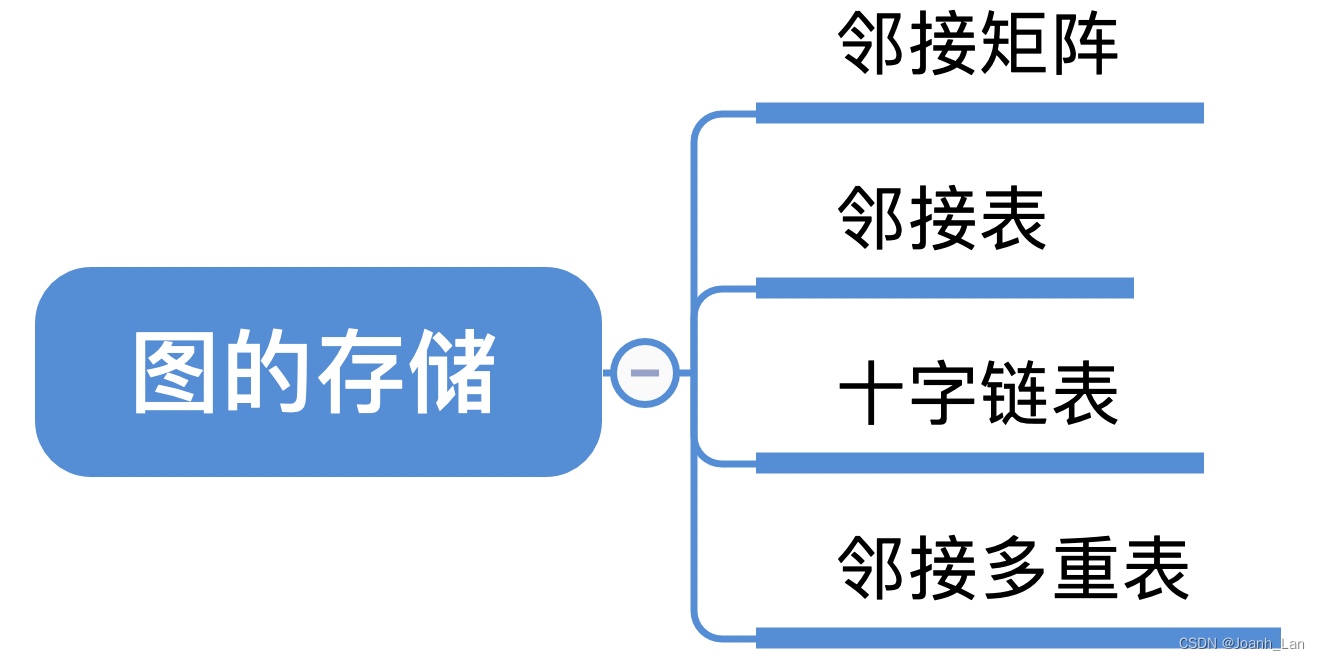
数据结构–图的存储邻接矩阵法

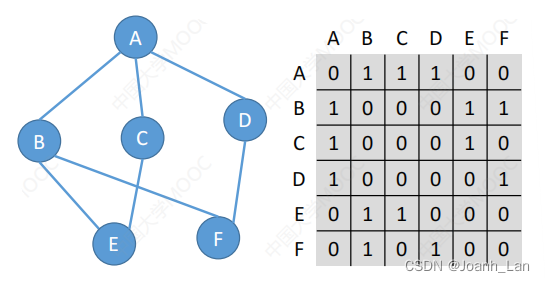
无向图：

有向图：

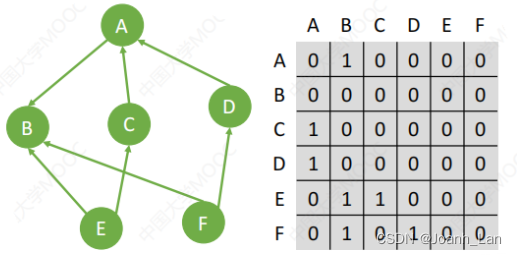
#define MaxVerTexNum 100 //顶点数目的最大值
typedef struct 
{
    char vex[MaxVerTexNum]; //顶点表
    int Edge[MaxVerTexNum][MaxVerTexNum]; //邻接矩阵，边表
    int vexnum, arcnum; //图的当前顶点数和边数/弧数
} MGraph;

无向图：
第i个结点的$度$ = $第i行（或第i列）$有向图的非零元素个数

有向图：
第i个结点的$出度$ = $第i行$的非零元素个数
第i个结点的$入度$ = $第i列$的非零元素个数
第i个结点的$度$ = $第i行、第i列$的非零元素个数之和

$邻接矩阵法求顶点的度/出度/入度的时间复杂度为O(|V|)$

邻接矩阵法存储带权图（网)

无向网:

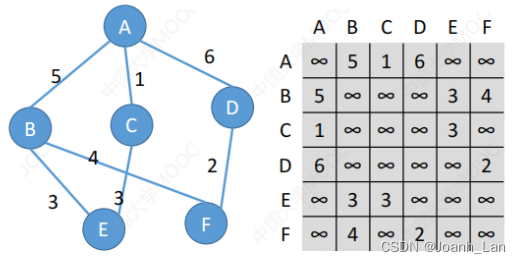
有向网:

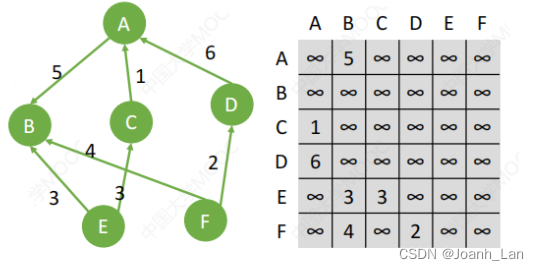
#define MaxVerTexNum 100 //顶点数目的最大值
#define INF 0x3f3f3f3f
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型

typedef struct 
{
    VertexType Vex[MaxVerTexNum]; //顶点
    EdgeType Edge[MaxVerTexNum][MaxVerTexNum]; //边的权
    int vexnum, arcnum; //图的当前顶点数和弧数
} MGraph;

邻接矩阵法的性能分析\

空间复杂度：$O(|V{|}^2)$ ——只和顶点数相关，和实际的边数无关
适合用于存储稠密图
无向图的邻接矩阵是对称矩阵，可以压缩存储（只存储上三角区/下三角区）

邻接矩阵法的性质

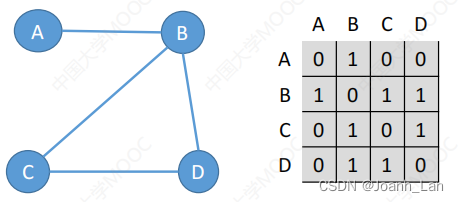
设图G的邻接矩阵为A（矩阵元素为0/1），则$A^n$的元素$A^n[i][j]$等于由顶点 i 到顶点 j 的长度为 n 的路径的数目

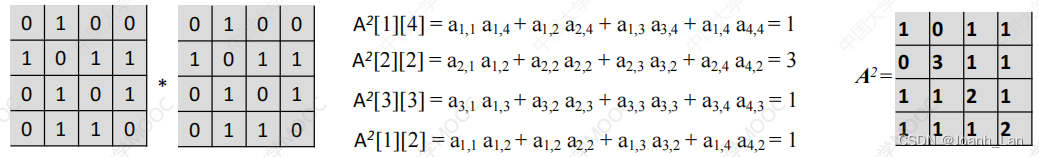
知识回顾与重要考点

邻接矩阵法要点回顾：
• 如何计算指定顶点的度、入度、出度（分无向图、有向图来考虑）？时间复杂度如何？
• 如何找到与顶点相邻的边（入边、出边）？时间复杂度如何？
• 如何存储带权图？
• 空间复杂度——$O(|V{|}^2)$，适合存储稠密图
• 无向图的邻接矩阵为对称矩阵，如何压缩存储？
• 设图G的邻接矩阵为A（矩阵元素为0/1），则An的元素An[i][j]等于由顶点i到顶点j的长度为n的路径的数目