Rivest-Shamir-Adleman (RSA) - 经典非对称加密算法
如果我们知道𝑝, 𝑞 (即𝑁 = 𝑝𝑞) 我们可以在mod N中进行反幂运算。
比如:
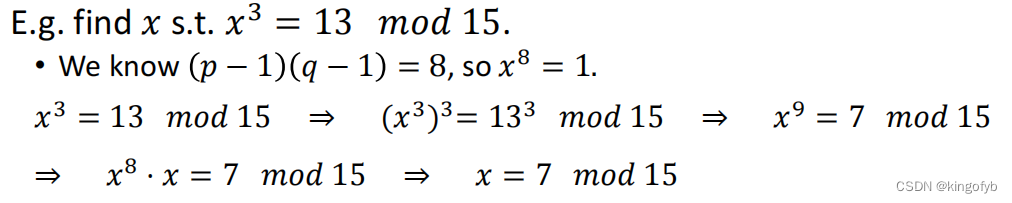
我们有一个单向陷门函数,非常适合加密。
“教科书式”RSA加密
- 取两个大素数,然后N = 𝑝𝑞, 然后挑选一对𝑒, 𝑑
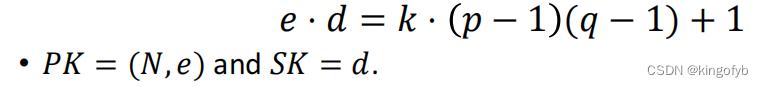
- 加密:给定𝑃𝐾 = (𝑁, 𝑒) 和一条消息𝑚 在里面
计算密文𝑐 :
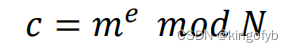
- 解密:给定一个密文𝑐 将原始消息计算为
![]()
- 运算过程
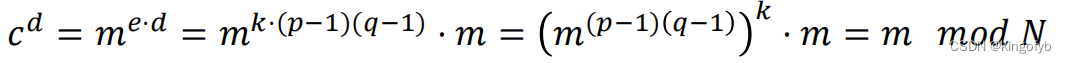
教科书式RSA加密并不是IND-CPA
教科书(又名Plain,Vanilla)RSA是确定性的,即相同的明文总是产生相同的密文,因此攻击者能够发现重复。
如果攻击者发现:
-
71F63EA被RSA加密为卖
-
6AE81B4被RSA加密为买
攻击者下次看到6AE81B4时就知道这是“购买”的加密。
教科书RSA满足了一周的安全概念:整个消息无法从密文中恢复。
修复教科书RSA
- 好的通用加密必须是概率性的,即每次加密明文时,都应该得到一个新的随机密文
- 确定性加密对于特殊目的非常有用,例如保留格式的加密
如果我们只是用随机填充来填充消息呢?
![]()
𝑟 需要足够长,才能让暴力破解不可行。
PKCS#1 v1.5使用了这个想法:
![]()
- 被认为是IND-CPA安全的
- CCA攻击是可能的,例如Bleichenbacher的攻击
Optimal Asymmetric Encryption Padding (OAEP) - RSA-OAEP

Factoring Hardness
在实践中,RSA模数大小为2048或3072位。
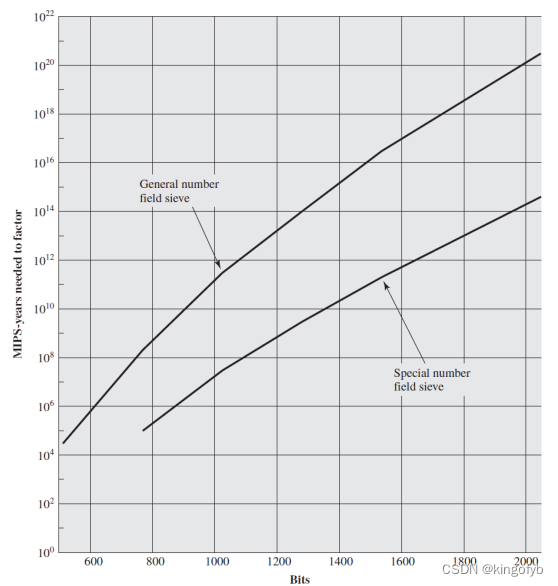
图片来源:Stallings
RSA中需要避免的其他问题
- 不要共用一个共同的模数 -- 共模攻击。
- 不要共用公共素数。公共素数可以通过有效的gcd算法找到,例如:
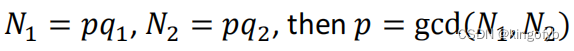
- 不要使用小公钥𝑒 加快加密速 -- 低加密指数攻击,尽管OAEP可以阻止此攻击
- 不要使用小密钥𝑑 以加快解密速度 -- 低解密指数攻击
NIST RSA密钥大小建议
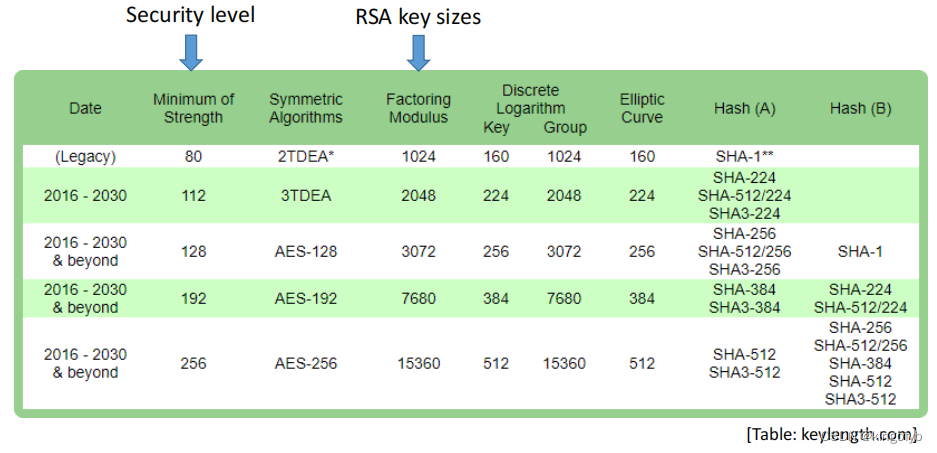
混合加密
公钥加密比对称加密慢得多,但不需要事先就共享密钥达成一致。
- 在实践中,几乎总是使用混合加密(也称为KEM-EM):
- 为对称加密生成新密钥
- 使用公钥加密对密钥进行加密(密钥封装机制)
- 使用对称加密和密钥来加密数据(数据封装机制)
比如:标准化DLIES/ECIES

混合加密的安全性和有效性
混合加密方案是IND-CPA安全的,如果
- 公钥加密方案PKEnc是IND-CPA安全的
- 对称加密方案SymEnc在窃听情况下无法区分
公钥加密方案
广泛使用:
- 基于因子分解:RSA家族、Rabin、Paillier
- 基于离散对数:ElGamal家族,Cramer–Shoup