Floyd算法学习笔记
前言
同步于 c n b l o g s cnblogs cnblogs 发布
如有错误,欢迎各位 dalao 批评指出。
前置芝士:
1.邻接矩阵(Floyd要用邻接矩阵存图)
2.动态规划思想(最好学过,没学过也没有太大影响)
1. Floyd 所解决问题的类型
我们可以发现,如 Dijkstra,SPFA,Bellman Ford 一类的最短路算法都是解决单源点最短路问题,也就是确定了起点或者终点来求最短路的问题。但是,我们发现,这些算法解决多源点最短路问题,也就是有多个起点和终点的最短路问题 ,的效率太低。假设有
n
n
n 个点,
m
m
m 条边。解决多源最短路时,如果用以上三种算法来解决,都需要分别做
n
n
n 次,来求解以每个点为起点的单源最短路,时间复杂度最慢分别是
O
(
n
m
l
o
g
n
)
,
O
(
n
2
m
)
,
O
(
n
2
m
)
O(nmlogn),O(n^2m),O(n^2m)
O(nmlogn),O(n2m),O(n2m),在稠密图
m
=
n
∗
(
n
−
1
)
/
2
≈
n
2
m=n*(n-1)/2≈n^2
m=n∗(n−1)/2≈n2其中最快的都需要
O
(
n
3
l
o
g
m
)
O(n^3logm)
O(n3logm) ,最慢的甚至是
O
(
n
4
)
O(n^4)
O(n4) ,效率太低。因此,我们今天的主角 Floyd 就因解决多源最短路问题而诞生了!
2. Floyd 的思想和基本做法
Floyd算法的基本思想是动态规划。
设 d p i j dp_{ij} dpij 表示 i i i 到 j j j 的最短距离。(有 n n n 个点)
首先对于这个 d p dp dp 数组的初始化就是将输入的边 x − y x-y x−y 权值为 z z z (无权图就是 1 1 1),如果图是无向,则 d p x y = d p y x = z dp_{xy}=dp_{yx}=z dpxy=dpyx=z ,如果图是有向,则 d p x y = z dp_{xy}=z dpxy=z,最后将所有 d p i i = 0 ( 0 ≤ i ≤ n ) dp_{ii}=0 (0\le i\le n) dpii=0(0≤i≤n),比较显然,这里不做解释。
接着我们进行状态转移。显然,我们要转移 d p i j dp_{ij} dpij,就需要找一个点 k k k,来进行转移,也就是 d p i j ← m i n ( d p i j , d p i k + d p k j ) dp_{ij}\gets min(dp_{ij},dp_{ik}+dp_{kj}) dpij←min(dpij,dpik+dpkj),其中 d p i k + d p k j dp_{ik}+dp_{kj} dpik+dpkj 就表示 i − k i-k i−k 的最短路与 j − k j-k j−k 的最短路之和,其实也就相当于一个松弛操作。
这里特别要注意的是:我们的 k k k 那一层循环一定要放在 i i i 和 j j j 两层循环之外,因为如果放在 i , j i,j i,j 以内的话,你就会发现每两个点的最短路只会被算到一次,而当你在进行状态转移时,你只算到一次的话,你会发现有些点在转移时,还没有被更新,就会出现没有求出最短路的情况,所以, k k k 的循环要放到 i , j i,j i,j 的循环之外。
Floyd算法由于
i
,
j
,
k
i,j,k
i,j,k 都要枚举一层循环,所以时间复杂度为
O
(
n
3
)
O(n^3)
O(n3),比开头讲的三个算法要快。
3.Floyd 代码实现
//n表示有n个点
memset(dp,0x3f,sizeof(dp));//赋一个极大值,并且防止在转移时不溢出。
//接下来进行边的初始化和dp[i][i]=0
............
//状态转移
for(int k=1;k<=n;++k)//枚举k
{
for(int i=1;i<=n;++i)//枚举i
{
if(i==k)//如果i,k个点相等,则不需要更新
continue;
for(int j=1;j<=n;++j)
{
if(i==j||k==j)//同第八行
continue;
dp[i][j]=min(dp[i][k]+dp[k][j],dp[i][j]);//状态转移。
}
}
}
4.Floyd 算法的一些其他应用
(1).Floyd 输出路径
对于输出路径,我们可以定义一个 p a t h i j path_{ij} pathij 表示 d p i j dp_{ij} dpij 是有 d p i p a t h i j + d p p a t h i j j dp_{ipath_{ij}}+dp_{path_{ij}j} dpipathij+dppathijj 转移而来。并且在一开始,我们将所有 p a t h path path 数组的元素赋一个特殊值。(假定为 − 1 -1 −1 )
显然,要输出 i − j i-j i−j 的路径,我们可以通过递归来解决。
具体代码如下:
//赋特殊值并且做 floyd
-----------
//输出路径函数
void print(int i,int j)//print(a,b) 表示输出a,b的最短路径
{
if(path[i][j]==-1)//因为开始初始化为-1,这里就可以避免相邻的再次输出
return;
print(i,path[i][j]);//前半部分
cout<<path[i][j]<<"-->";//输出该点
print(path[i][j],j);//后半部分
}
(2).Floyd 判断负环
在说这一个应用之前,我们先来讲一下负环的定义。
负环,就是指一个图中,存在一个环,使得这个环的权值之和为负数,这个环就是负环。
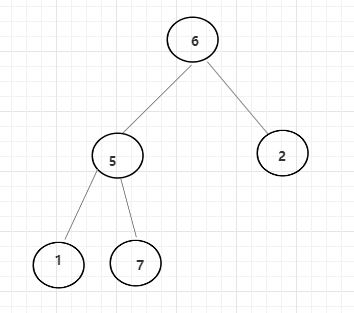
例如下图:
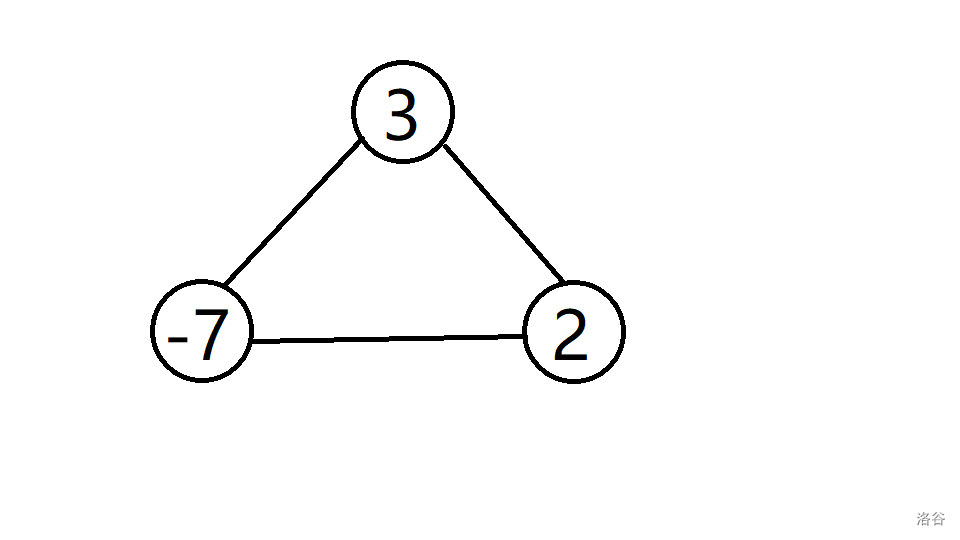
可以发现,由图中三个点组成的一个环的权值之和为负数,这就是一个简单的负环。
一个图中一旦存在负环,环里的两个点之间的最短路可以被无限更新,因为为了使得路径长度最短,它可以一直走这个负环,无限循环,这个最短路径就可以无限缩小。也就是说,一个图一旦存在负环,它的最短路就是 − ∞ -\infty −∞ ,也就相当于无解。
虽然说 SPFA Bellmanford 两个最短路算法可以判断负环,但是我们还是要讲一讲 Floyd 算法判断负环的方法。
因为负环可以使得两个点之间的最短路无限变小,所以我们可以发现,我们可以做两次 Floyd ,第一次来更新所谓的最短路,然后再做第二次的时候,如果两个点之间的最短路还可以被更新,就可以说明这个图中存在负环,比较显然。(自己想一想)。
第二次 Floyd 代码实现:
for(int k=1;k<=n;++k)
{
for(int i=1;i<=n;++i)
{
if(i==k)//同第一次
continue;
for(int j=1;j<=n;++j)
{
if(i==j||j==k)//同上
continue;
if(dp[i][j]>dp[i][k]+dp[k][j])//如果可以被更新,则存在负环
{
puts("No solution!");
}
}
}
}
(3).Floyd 判断有向图的连通性
我们知道,对于无向图的两个点是否联通,我们可以运用并查集来判断两个点是否联通。
但是对于一个有向图,并查集是不能够维护的,所以这个时候,我们就再一次请出今天的主角 Floyd 来判断两个点
i
,
j
i,j
i,j 是否连通。
我们定义 d p i j dp{ij} dpij 表示 i , j i,j i,j 是否连通,若联通则为 1 1 1 ,不连通则为 0 0 0 。
显然,我们可以根据 Floyd 一一样的方式进行初始化。一开始除了
d
p
i
i
dp_{ii}
dpii 全部赋值为
0
0
0 ,输入边的时候直接初始化即可。
接下来就是状态转移。我们可以模仿普通的 Floyd ,再找一个点
k
k
k ,如果
i
i
i 可以到达
k
k
k ,
k
k
k 可以到达
j
j
j ,就可以说明
i
i
i 可以到达
j
j
j ,转化成转移方程就是
d
p
i
j
∣
=
d
p
i
k
&
d
p
k
j
dp_{ij}|=dp_{ik}\&dp_{kj}
dpij∣=dpik&dpkj。
核心代码:
//n表示有n个点
memset(dp,0,sizeof(dp));//赋值。
//接下来进行边的初始化和dp[i][i]=1
............
//状态转移
for(int k=1;k<=n;++k)//枚举k
{
for(int i=1;i<=n;++i)//枚举i
{
if(i==k)//同上
continue;
for(int j=1;j<=n;++j)
{
if(i==j||k==j)//同上
continue;
dp[i][j]|=dp[i][k]&dp[k][j];//状态转移。
}
}
}
关于 Floyd 算法的讲解就到这里了,
s
e
e
y
o
u
see~ you
see you 。