文章目录
- 一、完全背包
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 二、322. 零钱兑换
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 三、518. 零钱兑换 II
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 四、279. 完全平方数
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 总结
一、完全背包
1.题目简介
DP42 【模板】完全背包
本题目来源于牛客网,大家可以点开上面的链接,进入题目页面进行练习。



2.解题思路
3.代码
#include <iostream>
using namespace std;
#include<vector>
int main() {
int n, V;
cin>>n;
cin>>V;
vector<int> v(n, 0);//存放物品到的体积
vector<int> w(n, 0);//存放物品的价值
for(int i = 0;i < n; ++i)
{
cin>>v[i];
cin>>w[i];
}
//问题1
vector<int> dp1(V + 1, 0);//dp[j]表示体积为j的背包至多能装多大价值的物品
for(int i = 0;i < n; ++i)
{
for(int j = v[i];j <= V; ++j)
{
dp1[j] = max(dp1[j - v[i]] + w[i], dp1[j]);
}
}
cout<<dp1[V]<<endl;
//问题2
vector<int> dp2(V + 1, -1);//dp[j]表示体积为j的背包至多能装多大价值的物品
dp2[0] = 0;//初始化体积为0时的dp值
for(int i = 0;i < n; ++i)
{
for(int j = v[i];j <= V; ++j)
{
if(dp2[j - v[i]] != -1)
{
dp2[j] = max(dp2[j - v[i]] + w[i], dp2[j]);
}
}
}
cout<<(dp2[V] == -1 ? 0 : dp2[V])<<endl;
return 0;
}
4.运行结果
二、322. 零钱兑换
1.题目简介
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。

2.解题思路
3.代码
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX);//dp[j]表示要凑成总金额为j所需要的硬币数
dp[0] = 0;//总金额为0的话,所需硬币数为0
for(int i = 0;i < coins.size(); ++i)
{
for(int j = coins[i];j <= amount; ++j)
{
if(dp[j - coins[i]] != INT_MAX)//如果等于INT_MAX说明该位置不能被合成,不能使用该位置
{
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
}
}
}
return (dp[amount] == INT_MAX ? -1 : dp[amount]);
}
};
4.运行结果

三、518. 零钱兑换 II
1.题目简介
518. 零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。


2.解题思路
3.代码
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int> dp(amount + 1, 0);//dp[j]表示凑成总金额为j的硬币组合数
//初始化
dp[0] = 1;//凑成0的硬币组合只有一种,就是一个硬币也没有;其他位置都初始化为0(为了避免影响结果)
for(int i = 0;i < coins.size(); ++i)
{
for(int j = coins[i];j <= amount; ++j)
{
if(dp[j - coins[i]] != 0)//如果等于-1,说明该位置无法凑出,所以不能使用该位置
dp[j] += dp[j - coins[i]];//要求组合数,因此要用+
}
}
return (dp[amount] == 0 ? 0 : dp[amount]);
}
};
4.运行结果
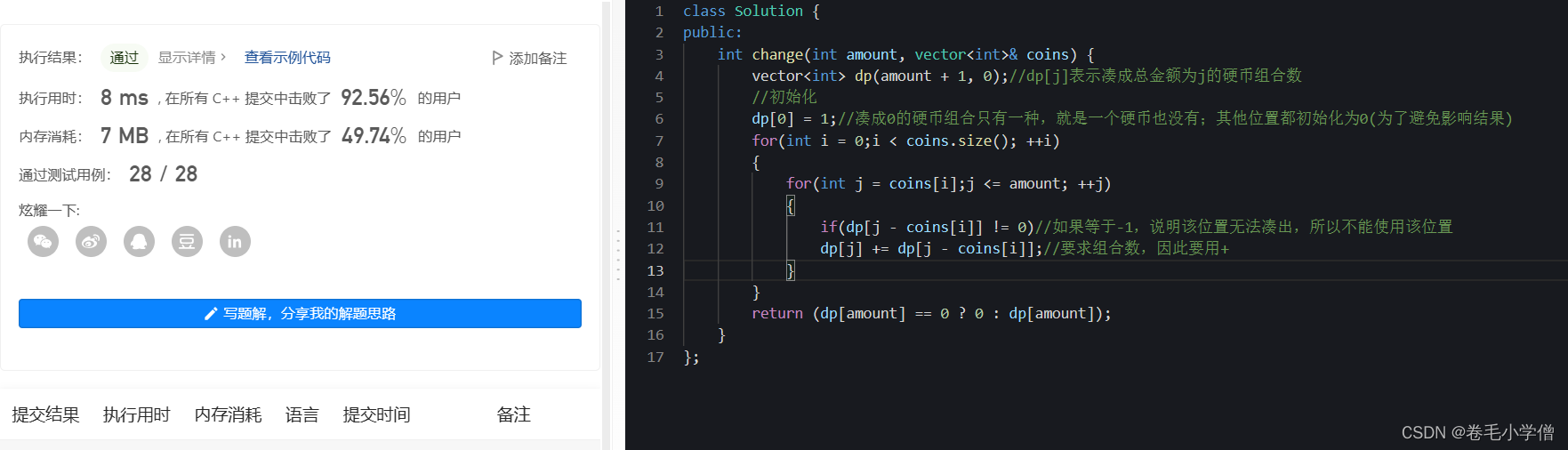
四、279. 完全平方数
1.题目简介
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。

2.解题思路
3.代码
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n + 1, INT_MAX);//dp[j]表示和为j的完全平方数的最少数量
dp[0] = 0;
//dp[0]初始化为0,和为0的完全平方数的数量为0
//其他位置全部初始化为INT_MAX,避免影响min的结果
for(int i = 1;i <= n; ++i)
{
for(int j = i * i;j <= n; ++j)
{
if(dp[j - i * i] != INT_MAX)//如果相等,说明该位置不能被组成,因此该位置不能被使用
dp[j] = min(dp[j - i * i] + 1, dp[j]);
}
}
return dp[n];
}
};
4.运行结果
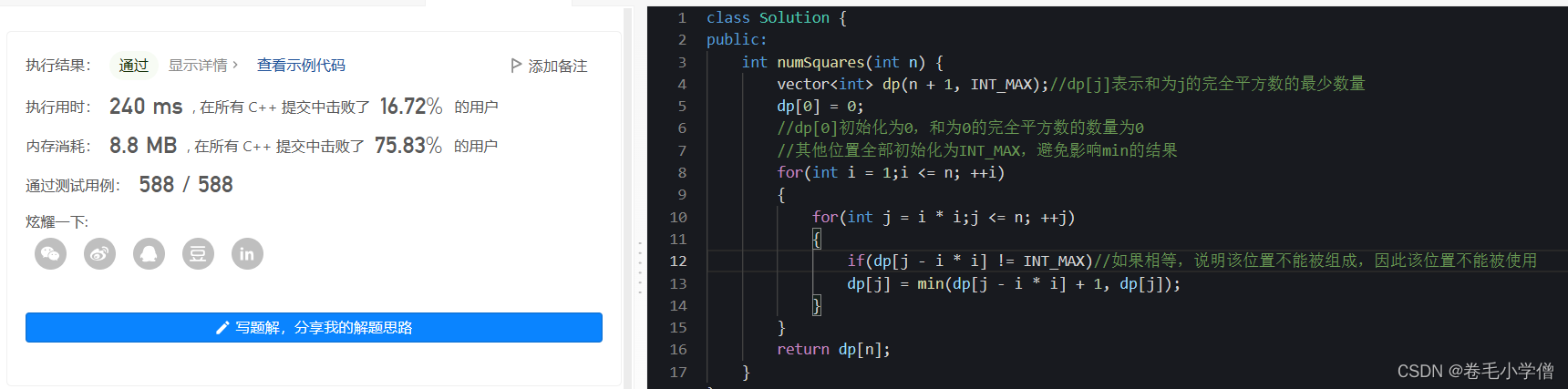
总结
今天是算法练习的第16天。
博观而约取,厚积而薄发 ,继续加油。
来源:力扣(LeetCode),著作权归领扣网络所有。
如果本篇文章对你有所启发的话,希望可以多多支持作者,谢谢大家!