前言:
- 大家好,我是良辰丫,第二十篇,牛客网选择题+编程题 字符串反转+公共子串计算(dp问题).💞💞💞
- 生活就像一只盲盒,藏着意想不到的辛苦,当然也有万般惊喜的可能。不管是次次都如愿以偿,还是赢面寥寥无几,终究起起伏伏才是常态。我们既有过顺遂,也难免绝望,但若一陷入困境就立即抽身而退,那就再也没有翻盘的可能。只要生活还在继续,就有赢的可能。
🧑个人主页:良辰针不戳
📖所属专栏:百日冲大厂
🍎励志语句:生活也许会让我们遍体鳞伤,但最终这些伤口会成为我们一辈子的财富。
💦期待大家三连,关注,点赞,收藏。
💌作者能力有限,可能也会出错,欢迎大家指正。
💞愿与君为伴,共探Java汪洋大海。

目录
- 1. 选择题
- 2. 编程题
- 2.1 字符串反转
- 2.2 公共子串计算
1. 选择题
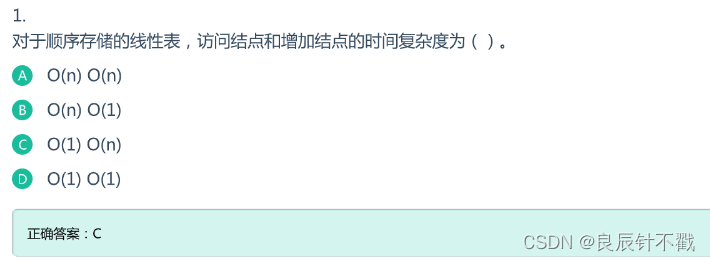
- 顺序存储的底层是数组.
- 数组可以根据下标快速定位元素,时间复杂度为O(1).
- 在某个地方增加节点的时候,得移动该位置后面的所有元素,因此时间复杂度为O(n)

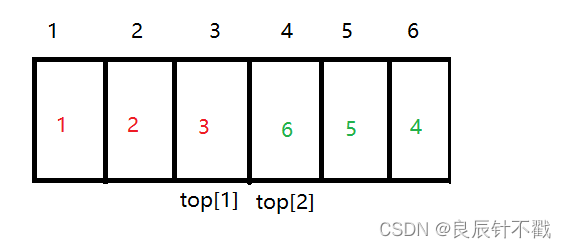
- top[i]表示第i个栈的栈顶,因此top[1]表示第一个栈的栈顶
- 第一个栈存元素从左开始,第二个栈存元素从右开始.
- 当数组没有存储空间的时候,元素就会满,此时两个栈的栈顶元素相邻,那么top[1]+1 = top[2]说明栈满了.
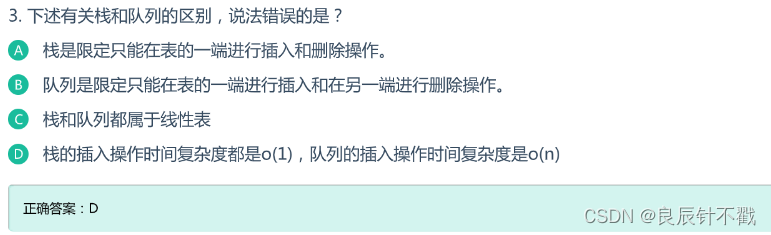
D中栈和队列的插入时间复杂度都是O(1).
- 这道题容易混淆的是回溯与递归.
- 递归是我们刚学代码基本就接触了,我们把函数自己调用自己的方式叫做递归,题目中老和尚给小和尚讲故事,就是重复同一件事情,因此我们可以把它看做递归.(但是递归往往有结束条件哈)
- 回溯经常用在深搜中,我们把回溯看做试探法,可以想象成迷宫探路,这条路走不通,返回去走下一条路.

n0 = n2 + 1;

前序遍历是根左右,中序遍历是左根右,二者遍历序列相同,那么没有左孩子,因此该二叉树为右单枝.

画图求解即可


这组数据接近排列后的数据,此时采用冒泡排序的方式比较快,因为冒泡排序在排列的时候发现数据没有交换的时候,它就已经有序了,跳出循环.

- 线性结构表示一对一.
- 树和图是非线性结构.
2. 编程题
2.1 字符串反转
做题链接:
链接: 字符串反转
题目描述:
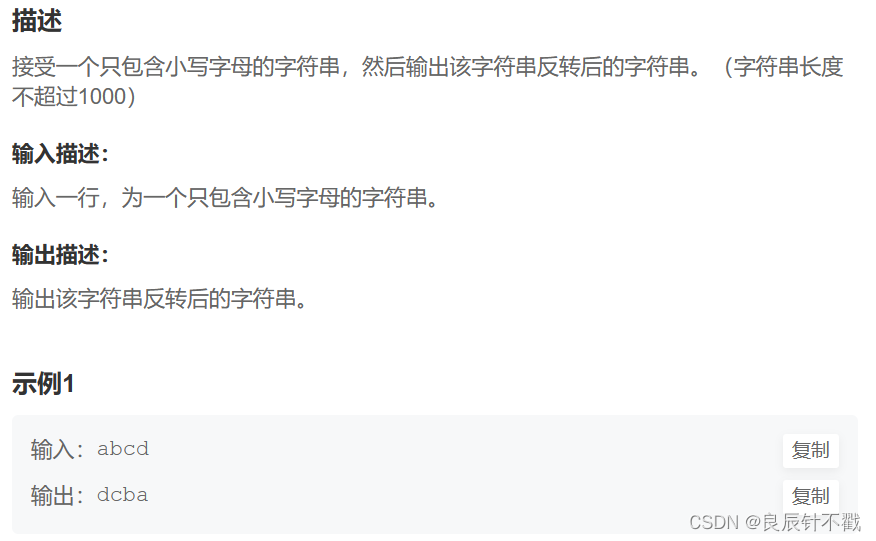
题目分析:
- 一看到字符串翻转我们就会想到双指针算法,一前一后交换元素.
- 代码比较简单,具体细节在代码中体现.
- 但是在这里我们解锁一个新知识,这里的结果要打印一个字符串,ch是一个字符数组,我们直接打印ch也可以,不用做无谓的转换.
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String str = in.nextLine();
char[] ch = str.toCharArray();
int left = 0;
int right = str.length()-1;
while(left < right){
char temp = ch[left];
ch[left] = ch[right];
ch[right] = temp;
left++;
right--;
}
//1. 第一种方式
// String str2 = new String(ch);
// System.out.println(str2);
//2. 第二种方式,ch是字符数组,但是也能这样使用
System.out.println(ch);
}
}
2.2 公共子串计算
做题链接:
链接: 公共子串计算
题目描述:
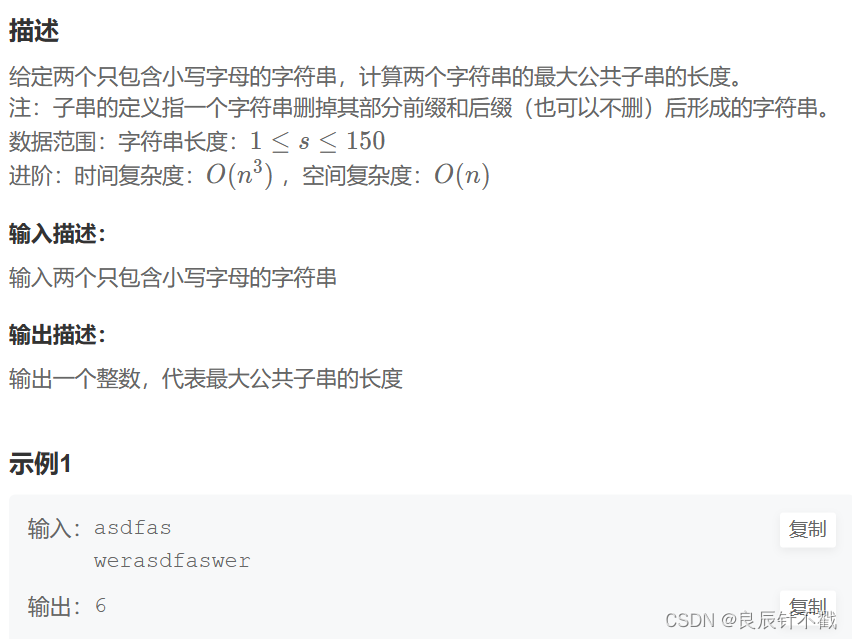
题目分析:
哎呦喂,又到了惊心动魄的动态规划题了,不要害怕,dp没有大家想的那么难,多做题多总结.
- 状态 : f(i,j) 表示a字符串以第 i 个字符结尾的串和b字符串以第 j 个字符结尾的串的最大公共子串的长度.
- 状态转移方程,如果a字符串的第 i 个字符与b字符串的第 j 个字符相同的时候f[i][j] = f[i-1 ][j-1 ] + 1,否则f[i][j] = 0.
- 返回值是最大公共子串的长度,我们只需要通过一个变量记录即可.
下面两种方式的代码都可以.
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String str1 = in.next();
String str2 = in.next();
char[] arr1 = new char[310];
for(int i = 1;i<=str1.length();i++){
arr1[i] = str1.charAt(i-1);
}
char[] arr2 = new char[160];
for(int i = 1;i<=str2.length();i++){
arr2[i] = str2.charAt(i-1);
}
int[][] f = new int[160][160];
// int begin = 0;
int len = 0;
//System.out.println(Arrays.toString(arr2));
for (int i = 1; i <= str1.length(); i++) {
for (int j = 1; j <= str2.length(); j++) {
//f[i][j] = Math.max(f[i-1][j],f[i][j-1]);
if (arr1[i] == arr2[j ]) {
f[i][j] = f[i-1 ][j-1 ] + 1;
} else{
f[i][j] = 0;
}
len = Math.max(f[i][j],len);
}
}
//String str3 = str1.substring(start,start+maxLen);
System.out.println(len);
}
}
import java.io.*;
import java.util.*;
public class Main
{
public static int getMaxLen(String str1, String str2)
{
char[] arr1 = str1.toCharArray();
char[] arr2 = str2.toCharArray();
int len1 = arr1.length;
int len2 = arr2.length;
int[][] maxSubLen = new int[len1 + 1][len2 + 1];
int maxLen = 0;
for(int i = 1; i <= len1; ++i)
{
for(int j = 1; j <= len2; ++j)
{
if(arr1[i - 1] == arr2[j - 1])
{
//F(i,j) = F(i - 1, j - 1) + 1
maxSubLen[i][j] = maxSubLen[i - 1][j - 1] + 1;
//更新最大值
if(maxLen < maxSubLen[i][j])
{
maxLen = maxSubLen[i][j];
}
}
}
}
return maxLen;
}
public static void main(String[] args) throws Exception
{
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String str1;
String str2;
while((str1 = reader.readLine()) != null)
{
str2 = reader.readLine();
System.out.println(getMaxLen(str1, str2));
}
}
}