每日一题：折半查找法，二分查找法

​ 💖💖个人博客:比昨天强一点， 昨天强一点就好的博客💖💖

​ 💖💖多年再寒暄，所遇非故人💖💖

二分查找法定义：

先看折半查找的定义：

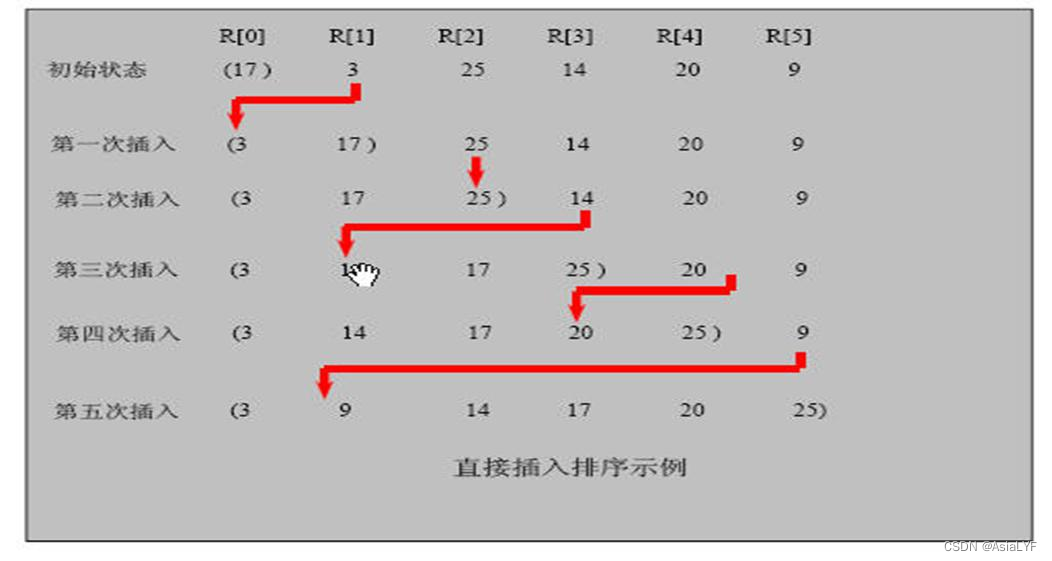
折半查找法是效率较高的一种查找方法。假设有已经按照从小到大的顺序排列好的五个整数a0~a4，要查找的数是X，其基本思想是： 设查找数据的范围下限为l=0，上限为h=4，求中点m=(l+h)/2，用X与中点元素am比较，若X等于am,即找到，停[查找,否则，若X大于am，替换下限l=m+1，到下半段继续查找；若X小于am，换上限h=m-1，到上半段继续查找；如此重复前面的过程直到找到或者l>h为止。如果l>h，说明没有此数，打印找不到信息，程序结束。该方法是查找的范围不断缩小一半，所以查找效率较高。

更加详细的概念：折半查找法_百度百科 (baidu.com)

看概念可能有点懵，我们来理解一下：

注意，注意，注意！！！折半查找法有个硬性条件：必须是有序的数列（升序降序均可）

理解了方法，可能觉得其实也没什么，而且还必须是有序的数列才能使用，但是千万不要小瞧了这个方法，现在数字很少你可能觉得没什么厉害的，但是如果你格局打开一点，

假设有1亿个数字，一次就可以干掉一半，这还是很恐怖的了，与遍历方法相比在时间复杂度上可想而知。

下面我们来看代码：

代码1：

//二分查找法
//折半查找法

//找出数字7并且打印下标
#include<stdio.h>

int main()
{
	int flag = 0;
	printf("请输入要查找的数字:>\n");
	scanf("%d", &flag);
	int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	int left = 0;
	int right = sz - 1;
	while (left <= right)
	{
		int mid = (left + right) / 2;
		if (arr[mid] < flag)
		{
			left = mid + 1;
		}
		else if (arr[mid] > flag)
		{
			right = mid-1;
		}
		else if(arr[mid]==flag)
		{
			printf("找到了，数字%d的下标是:%d\n",flag, mid);
			break;
		}
	}
	if (left > right)
	{
		printf("找不到\n");
	}
	return 0;
}

当然了，我们也可以用函数来实现：

代码2：

//写一个函数实现二分查找

#include<stdio.h>

int half_find(int* arr, int left, int right,int key)
{
	while (left <= right)
	{
		int mid = (left + right) / 2;
		if (arr[mid] < key)
		{
			left = mid + 1;
		}
		else if (arr[mid] > key)
		{
			right = mid - 1;
		}
		else if (arr[mid] == key)
		{
			return mid;
		}
	}
	return 0;
}

int main()
{
	int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	int key = 0;
	printf("请输入要查找的元素:>\n");
	scanf("%d", &key);
	int flag=half_find(arr, 0, sz - 1,key);
	if (flag == 0)
	{
		printf("找不到\n");
	}
	else
	{
		printf("找到了,下标是:%d\n", flag);
	}
	return 0;
}