六、排序算法介绍2

news2024/11/18 23:36:33

1、冒泡排序

1.1 基本介绍

  • 冒泡排序（Bubble Sorting） 的基本思想是： 通过对待排序序列从前向后（从下标较小的元素开始），依次比较相邻元素的值， 若发现逆序则交换， 使值较大的元素逐渐从前移向后部， 就像水底下的气泡一样逐渐向上冒。
  • 优化：因为排序的过程中， 各元素不断接近自己的位置， 如果一趟比较下来没有进行过交换， 就说明序列有序， 因此要在排序过程中设置一个标志 flag 判断元素是否进行过交换。 从而减少不必要的比较。 (这里说的优化， 可以在冒泡排序写好后， 再进行)

1.2 冒泡排序图解

  • 第一趟：
    从数组 arr 第一个元素开始，与其后面一个元素比较大小
    如果 arr[i] > arr[i+1] ，则交换，将大的元素换到后面去
    由于是当前元素与其后面一个元素比较大小，所以只需要执行 arr.length - 1 次循环
  • 第二趟：
    从数组 arr 第一个元素开始，与其后面一个元素比较大小
    由于第一趟排序完成，数组最后一个元素已是最大元素，所以只需要执行 arr.length - 1 - 1 次循环

啥时候完成？下面两个条件满足任意一个即可：
当其中有一趟排序没有元素交换位置时，说明数组已经有序
或：按照上述流程，跑完第 arr.length - 1 趟之后
这样来想：5 个元素的数组，最多只需要跑 4 趟
为什么最多只需要跑 4 趟？因为跑完 4 趟之后，数组第二个元素已经成为了数组第二小的元素，那么数组自然就是有序数组
即数组长度如果为 n ，那么则需要跑 n - 1 趟

1.3 代码实现

public class BubbleSort {

	public static void main(String[] args) {
		int[] arr = {3,9,-1,10,-2};
		bubbleSort(arr);
		System.out.println("排序后:"+Arrays.toString(arr));
	}
	
	/**
	 * 冒泡排序  时间复杂度o(n^2)
	 * @param arr
	 */
	private static void bubbleSort(int[] arr) {
		int temp ;
		for (int i = 0; i < arr.length -1; i++) {
			for (int j = 0; j < arr.length -1 - i; j++) {
				if (arr[j] > arr[j+1]) {
					temp = arr[j];
					arr[j] = arr[j+1];
					arr[j+1] = temp;
				}
			}
		}
	}
}

1.4 优化后的代码实现

public class BubbleSort {

	public static void main(String[] args) {
		int[] arr = {3,9,-1,10,20};
		bubbleSort(arr);
		System.out.println("排序后:"+Arrays.toString(arr));
	}
	
	/**
	 * 冒泡排序  时间复杂度o(n^2)
	 * @param arr
	 */
	private static void bubbleSort(int[] arr) {
		int temp ;
		boolean flag = false;//表示是否进行过交换
		for (int i = 0; i < arr.length -1; i++) {
			for (int j = 0; j < arr.length -1 - i; j++) {
				if (arr[j] > arr[j+1]) {
					flag = true;
					temp = arr[j];
					arr[j] = arr[j+1];
					arr[j+1] = temp;
				}
			}
			System.out.println("第" + (i + 1) + "趟排序后的数组");
	 		System.out.println(Arrays.toString(arr));
			if (!flag) {
				//在一趟排序中，一次交换都没有发生过
				break;
			}else {
				//重置flag!!!, 进行下次判断
				flag = false;
			}
		}
	}
}

1.5 测试冒泡排序性能

public class BubbleSort {

	public static void main(String[] args) {
		
		int[] arr = new int[80000];
		for (int i = 0; i < 80000; i++) {
			arr[i] = (int)(Math.random()*8000000);
		}
		
		Date date1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String before = simpleDateFormat.format(date1);
		System.out.println("排序前的时间是=" + before);
		
		bubbleSort(arr);
		
		Date date2 = new Date();
		String after = simpleDateFormat.format(date2);
		System.out.println("排序后的时间是=" + after);
	}
	
	/**
	 * 冒泡排序  时间复杂度o(n^2)
	 * @param arr
	 */
	private static void bubbleSort(int[] arr) {
		int temp ;
		boolean flag = false;//表示是否进行过交换
		for (int i = 0; i < arr.length -1; i++) {
			for (int j = 0; j < arr.length -1 - i; j++) {
				if (arr[j] > arr[j+1]) {
					flag = true;
					temp = arr[j];
					arr[j] = arr[j+1];
					arr[j+1] = temp;
				}
			}
			if (!flag) {
				//在一趟排序中，一次交换都没有发生过
				break;
			}else {
				//重置flag!!!, 进行下次判断
				flag = false;
			}
		}
	}
}

程序运行结果：

排序前的时间是=2022-12-07 08:55:42
排序后的时间是=2022-12-07 08:55:52

2、选择排序

2.1 基本介绍

选择式排序也属于内部排序法， 是从欲排序的数据中， 按指定的规则选出某一元素， 再依规定交换位置后达到排序的目的。

2.2 排序思想

选择排序（select sorting） 也是一种简单的排序方法。 它的基本思想是（n 是数组大小）：

  • 第一次从 arr[0]~arr[n-1]中选取最小值，与 arr[0] 交换
  • 第二次从 arr[1]~arr[n-1]中选取最小值， 与 arr[1] 交换
  • 第三次从 arr[2]~arr[n-1]中选取最小值， 与 arr[2] 交换
  • 第 i 次从 arr[i-1]~arr[n-1]中选取最小值， 与 arr[i-1] 交换
  • 第 n-1 次从 arr[n-2]~arr[n-1]中选取最小值，与 arr[n-2] 交换
  • 总共通过 n-1 次， 得到一个按排序码从小到大排列的有序序列

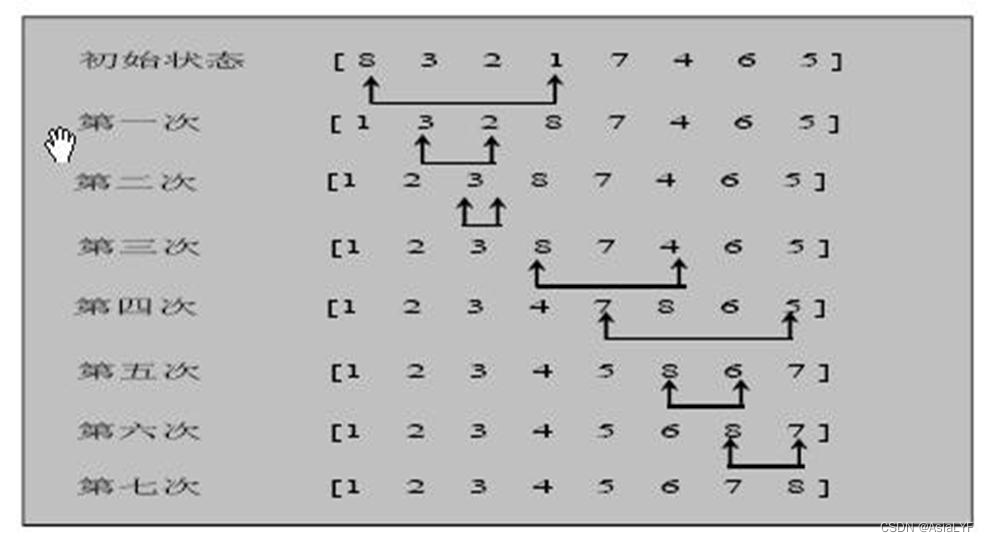
2.3 排序图解

  • 选择排序流程：
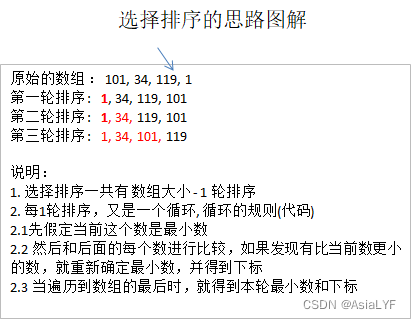
    第一次循环，默认 arr[0] 是最小的元素，将其与 arr[1]~arr[n-1] 进行比较，找到最小的元素，并与 arr[0] 的位置位置
    第二次循环，默认 arr[1] 是最小的元素，将其与 arr[2]~arr[n-1] 进行比较，找到最小的元素，并与 arr[1] 的位置位置
    第 i 次循环，默认 arr[i] 是最小的元素，将其与 arr[i+1]~arr[n-1] 进行比较，找到最小的元素，并与 arr[i] 的位置位置
    直到循环执行 n - 1 次

  • 总结：两层 for 循环

    第一层 for 循环控制走多少趟：for (int i = 0; i < arr.length - 1; i++) {
    从数组第一个元素开始，因为每次都是拿当前元素 arr[j] 和其后一个元素 arr[j+1] 进行比较
    到数组倒数第二个元素结束，将 arr[arr.length - 2] 与 arr[arr.length - 1] 进行比较后，数组就已经是有序数组
    如果数组大小为 n ，那么执行完第 n - 1 趟时，数组就已经是有序数组
    第二层 for 循环控制从第几个元素开始执行选择排序：for (int j = i + 1; j < arr.length; j++)
    每次进入第二层 for 循环时，先假设当前元素 arr[i] 是最小的元素：min = arr[i]; ，并记录最小元素的下标：index = i;
    然后依次和其后面的元素 arr[j] 比较，如果找到比 arr[i] 小的元素，则更新最小值和最小值的索引：min = arr[j]; index = j ;
    在这里插入图片描述
    在这里插入图片描述

2.4 代码实现

  • 一步一步理解选择排序算法
//选择排序
public class SelectSort {

	public static void main(String[] args) {
        
		int[] arr = { 101, 34, 119, 1 };
		selectSort(arr);
        
	}

	// 选择排序
	public static void selectSort(int[] arr) {
        
		// 使用逐步推导的方式来，讲解选择排序
		// 第1轮
		// 原始的数组 ： 101, 34, 119, 1
		// 第一轮排序 : 1, 34, 119, 101
		// 算法 先简单--》 做复杂， 就是可以把一个复杂的算法，拆分成简单的问题-》逐步解决

		// 第1轮
		int minIndex = 0;
		int min = arr[0];
		for (int j = 0 + 1; j < arr.length; j++) {
			if (min > arr[j]) { // 说明假定的最小值，并不是最小
				min = arr[j]; // 重置min
				minIndex = j; // 重置minIndex
			}
		}
		// 将最小值，放在arr[0], 即交换
		if (minIndex != 0) {
			arr[minIndex] = arr[0];
			arr[0] = min;
		}
		System.out.println("第1轮后~~");
		System.out.println(Arrays.toString(arr));// 1, 34, 119, 101

		// 第2轮
		minIndex = 1;
		min = arr[1];
		for (int j = 1 + 1; j < arr.length; j++) {
			if (min > arr[j]) { // 说明假定的最小值，并不是最小
				min = arr[j]; // 重置min
				minIndex = j; // 重置minIndex
			}
		}
		// 将最小值，放在arr[0], 即交换
		if (minIndex != 1) {
			arr[minIndex] = arr[1];
			arr[1] = min;
		}
		System.out.println("第2轮后~~");
		System.out.println(Arrays.toString(arr));// 1, 34, 119, 101

		// 第3轮
		minIndex = 2;
		min = arr[2];
		for (int j = 2 + 1; j < arr.length; j++) {
			if (min > arr[j]) { // 说明假定的最小值，并不是最小
				min = arr[j]; // 重置min
				minIndex = j; // 重置minIndex
			}
		}
		// 将最小值，放在arr[0], 即交换
		if (minIndex != 2) {
			arr[minIndex] = arr[2];
			arr[2] = min;
		}
		System.out.println("第3轮后~~");
		System.out.println(Arrays.toString(arr));// 1, 34, 101, 119
	}

}
  • 编写选择排序
//选择排序
public class SelectSort {

	public static void main(String[] args) {
		int[] arr = { 101, 34, 119, 1 };
		selectSort(arr);
	}

	// 选择排序
	public static void selectSort(int[] arr) {

		// 在推导的过程，我们发现了规律，因此，可以使用for来解决
		// 选择排序时间复杂度是 O(n^2)
		for (int i = 0; i < arr.length - 1; i++) {
			int minIndex = i;
			int min = arr[i];
			for (int j = i + 1; j < arr.length; j++) {
				if (min > arr[j]) { // 说明假定的最小值，并不是最小
					min = arr[j]; // 重置min
					minIndex = j; // 重置minIndex
				}
			}

			// 将最小值，放在arr[0], 即交换
			if (minIndex != i) {
				arr[minIndex] = arr[i];
				arr[i] = min;
			}

			System.out.println("第" + (i + 1) + "轮后~~");
			System.out.println(Arrays.toString(arr));
		}

	}
}

2.5 测试选择排序性能

public class SelectSort {

	public static void main(String[] args) {
		int[] arr = new int[80000];
		for (int i = 0; i < 80000; i++) {
			arr[i] = (int)(Math.random()*8000000);
		}
		
		Date date1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String before = simpleDateFormat.format(date1);
		System.out.println("排序前的时间是=" + before);
		
		selectSort(arr);
		
		Date date2 = new Date();
		String after = simpleDateFormat.format(date2);
		System.out.println("排序后的时间是=" + after);
	}

	/**
	 * 选择排序
	 * @param arr
	 */
	private static void selectSort(int[] arr) {
		for (int i = 0; i < arr.length - 1; i++) {
			//假定最小的
			int minIndex = i;
			int min = arr[i];
			for (int j = i + 1; j < arr.length; j++) {
				if (min > arr[j]) {
					minIndex = j;
					min = arr[j];
				}
			}
			//开始交换
			if (minIndex != i) {
				arr[minIndex] = arr[i];
				arr[i] = min;
			}
		}
	}
}

程序运行结果：

排序前的时间是=2022-12-07 08:58:09
排序后的时间是=2022-12-07 08:58:10

2.6 总结

由于选择排序算法在最内层的 for 循环中，满足 if (min > arr[j]) { 条件后，只需要记录最小值和最小值在数组中的索引，无需像冒泡排序那样每次都要执行交换操作，所以选择排序算法的执行速度比冒泡排序算法快一些

3、插入排序

3.1基本介绍

插入式排序属于内部排序法，是对于欲排序的元素以插入的方式找寻该元素的适当位置，以达到排序的目的。

3.2 插入排序法思想

  • 插入排序（Insertion Sorting） 的基本思想是： 把 n 个待排序的元素看成为一个有序表和一个无序表
  • 开始时有序表中只包含一个元素， 无序表中包含有 n-1 个元素， 排序过程中每次从无序表中取出第一个元素， 把它的排序码依次与有序表元素的排序码进行比较， 将它插入到有序表中的适当位置， 使之成为新的有序表

3.3 插入排序图解

3.3.1 插入排序逻辑
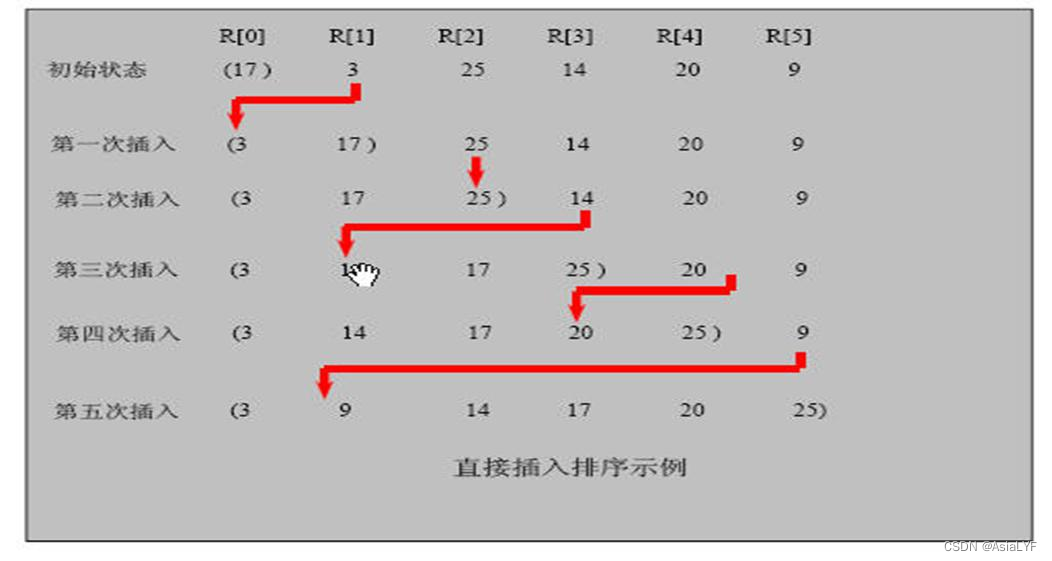
  • 将数组分为两个数组，前部分有序数组，后部分是无序数组，我们的目的就是一点一点取出无序数组中的值，将其放到有序数组中去
  • 第一趟：arr[0] 作为有序数组的元素，arr[1] 作为无序数组中第一个元素，将 arr[1] 与 arr[0] 进行比较，目标是将 arr[1] 插入到有序数组中
  • 第二趟：arr[0] 和 arr[1] 作为有序数组的元素，arr[2] 作为无序数组中第一个元素，将 arr[2] 与 arr[0] 和 arr[1] 比较，目标是将 arr[2] 插入到有序数组中
  • 第 i 趟：arr[0]~arr[i] 作为有序数组的元素，arr[i+1] 作为无序数组中第一个元素，将 arr[i+1] 与 arr[0]~arr[i] 比较，目标是将 arr[i+1] 插入到有序数组中
  • 第 n-1 趟：此时有序数组为 arr[0]~arr[n-2] ，无序数组为 arr[n-1] ，将无序数组中最后一个元素插入到有序数组中即可
3.3.2 如何进行插入？
  • 假设有个指针（index），指向无序数组中的第一个元素，即 arr[index] 是无序数组中的第一个元素，我们定义一个变量来存储该值：int insertVal = arr[index];，现在要将其插入到前面的有序数组中
  • 将 index 前移一步，则指向有序数组最后一个元素，我们定义一个新的变量来存储该指针：insertIndex = index - 1; ，即 arr[insertIndex] 是有序数组最后一个元素
  • 我们需要找到一个比 insertVal 小的值，并将 insertVal 插入在该值后面：
    ①如果 insertVal > arr[insertIndex] ，执行插入
    ②如果 insertVal < arr[insertIndex] ，将有序数组后移，腾出插入空间，insertIndex 指针前移，再看看前一个元素满不满足条件，直到找到插入位置
    ③即循环终止条件为找到插入位置，又分为两种情况：
    （1）在有序数组中间找到插入位置
    （2）insertVal 比有序数组中所有的数都小，插入在数组第一个位置（insertIndex = 0 的情况）
3.3.3 总结
  • for 循环控制走多少趟：for(int i = 1; i < arr.length; i++) { ，从数组第一个元素开始到数组最后一个元素结束
  • while 循环不断将指针前移，在有序数组中寻找插入位置，并执行插入：
    while (insertIndex >= 0 && insertVal < arr[insertIndex])
    在这里插入图片描述

3.4 代码实现

3.4.1 插入排序分步实现

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/72471.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

netcore接入钉钉扫码登录

netcore接入钉钉扫码登录

netcore接入钉钉扫码登录一、首先官方文档预览二、登录钉钉开发者后台三、创建第三方登录授权应用1.新版打开方式2.旧版打开方式&#xff08;1&#xff09;先返回旧版页面&#xff08;2&#xff09;选择应用开发&#xff08;3&#xff09;编辑登录应用信息&#xff08;4&#x…
阅读更多...
npm包是什么？如何发布npm包？

npm包是什么？如何发布npm包？

Node的组成 内置模块 自定义模块 第三方模块&#xff08;什么是包&#xff1f;&#xff09; npm包包括那些东西&#xff1f; package.json README.md 。。。.js 注册npm账号 细节 发布包 package.json README.md index.js date htmlEscape 层级结构 发布指令 N…
阅读更多...
STC15 - C51 - Memory Models

STC15 - C51 - Memory Models

文章目录STC15 - C51 - Memory Models概述笔记内存用量的优化思路ENDSTC15 - C51 - Memory Models 概述 在STC上测试呢, 想看看变量(不同类型的定义)被编译器分配在哪个内存范围(idata, pdata, xdata)? 同时, 总结一下降低内存用量的思路(如果像上位机那样内存管够, 就不用考…
阅读更多...
Linux系统编程第五节——进程创建、终止、等待（通俗易懂快速上手版本）

Linux系统编程第五节——进程创建、终止、等待（通俗易懂快速上手版本）

目录 进程的创建 写时拷贝 进程的终止 进程的等待 状态参数status wait函数和waitpid函数 我们本节内容&#xff0c;主要来讲述进程控制有关的内容。 同样&#xff0c;我们会用通俗易懂、不同于教科书的讲授思路&#xff0c;来为大家讲解。 同时&#xff0c;本节内容板块…
阅读更多...
你了解你的身体吗？- 基因社会

你了解你的身体吗？- 基因社会

关于作者 本书的两位作者分别是以太•亚奈和马丁 • 菜凯尔&#xff0c;前者是哈佛大学髙级研究学者&#xff0c; 任职于纽约大学&#xff0c;是生物化学和分子药理 学的教授&#xff1b;后者是杜塞尔多夫海因西里•海 涅大学的生物信息学教授。两位作者从基 因之间合作和竞争…
阅读更多...
[附源码]计算机毕业设计的4s店车辆管理系统Springboot程序

[附源码]计算机毕业设计的4s店车辆管理系统Springboot程序

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
5款十分好用，但是没有什么知名度的软件

5款十分好用，但是没有什么知名度的软件

随着网络信息技术的发展&#xff0c;越来越多的人在办公时需要用到电脑了。如果你想提高办公效率&#xff0c;那么就少不了工具的帮忙&#xff0c;今天给大家分享5款办公必备的好软件。 1.数据可视化软件——Power BI Power BI是一款出色的业务分析软件。Power BI主要是用于在…
阅读更多...
[Go] go基础4

[Go] go基础4

1. 并发编程 1.1 并发和并行 并发: 多个线程在同个核心的CPU上运行.并发的本质是串行. 并行: 多个线程在多个核心的CPU上运行. 1.2 协程和线程 协程: 独立的栈空间,共享堆空间,调度由用户控制,本质上有点类似用户及线程,这些用户及线程的调度也是自己实现的. 线程: 一个线…
阅读更多...
[附源码]JAVA毕业设计网络饮品销售管理系统（系统+LW）

[附源码]JAVA毕业设计网络饮品销售管理系统（系统+LW）

[附源码]JAVA毕业设计网络饮品销售管理系统&#xff08;系统LW&#xff09; 项目运行 环境项配置&#xff1a; Jdk1.8 Tomcat8.5 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目…
阅读更多...
全新社交电商模式来袭，消费增值结合共享经济完成消费升级

全新社交电商模式来袭，消费增值结合共享经济完成消费升级

大家好&#xff0c;我是林工&#xff0c;不知道大家是否了解消费增值&#xff1f;这是一个消费储量为基础的理念&#xff0c;体现的是消费者的消费与回报问题&#xff0c;普遍的消费返利&#xff0c;消费全返渐渐地已经不能够满足目前的客户&#xff0c;也就有了一个满足与这部…
阅读更多...
【嵌入式硬件芯片开发笔记】4-20mA DAC芯片AD5421配置流程

【嵌入式硬件芯片开发笔记】4-20mA DAC芯片AD5421配置流程

【嵌入式硬件芯片开发笔记】4-20mA DAC芯片AD5421配置流程 16位、串行输入、环路供电、4 mA至20 mA DAC 可用于HART协议相关电路 同AD5700配合使用 AD5421的SPI和普通的不一样 回读时要发两段 CS中间拉高一次 数据在SCLK上升沿逐个输出&#xff0c;而且在 SCLK下降沿有效 固CP…
阅读更多...
使用方法丨艾美捷Caspase-1活性分析试剂盒介绍

使用方法丨艾美捷Caspase-1活性分析试剂盒介绍

如何动态检测活细胞内的Caspase-1的活性&#xff0c;做更真实的实验&#xff1f;艾美捷推荐Immunochemistry Tech&#xff08;ICT&#xff09;的FLICA系列科研工具&#xff0c;轻松检测活细胞Caspase-1 活性。 艾美捷Immunochemistry Caspase-1活性分析试剂盒原理&#xff1a…
阅读更多...
Qt第三十四章：总结【隐藏标题栏边框、隐藏背景、窗体透明】

Qt第三十四章：总结【隐藏标题栏边框、隐藏背景、窗体透明】

目录 隐藏标题栏边框 ①隐藏标题栏代码&#xff1a; ​编辑②自定义标题栏(可以直接Copy) 使用 隐藏背景 ①隐藏背景代码,此时背景上的样式都是无效的。 ②自定义背景,通过重写paintEvent事件来完成 中间绘制的部分是我们想要的&#xff0c;只需要将标题栏边框隐藏掉就可…
阅读更多...
五、卷积神经网络CNN5（图像卷积与反卷积）

五、卷积神经网络CNN5（图像卷积与反卷积）

图像卷积 首先给出一个输入输出结果那他是怎样计算的呢&#xff1f; 卷积的时候需要对卷积核进行 180 的旋转&#xff0c;同时卷积核中心与需计算的图像像素对齐&#xff0c;输出结构为中心对齐像素的一个新的像素值&#xff0c;计算例子如下&#xff1a;这样计算出左上角(即第…
阅读更多...
【畅购商城】内网穿透之EchoSite

【畅购商城】内网穿透之EchoSite

目录 概述 注册用户 抢注域名 ​​​​​​​下载客户端 ​​​​​​​编写配置文件 ​​​​​​​启动 ​​​​​​​访问 ​​​​​​​概述 EchoSite一款收费的内网映射工具&#xff08;已下架&#xff09; 花生壳&#xff1a;内网穿透工具&#xff0c;免费版…
阅读更多...
springboot集成Lombok、MybaitsPlus、SwaggerUI

springboot集成Lombok、MybaitsPlus、SwaggerUI

springboot集成Lombok、MybaitsPlus、SwaggerUI 基础环境&#xff1a;JDK8或者JDK11版本 Maven3.5(采⽤默认) IDEA旗舰版 Mysql5.7以上版本 创建springboot项目 在线构建⼯具 https://start.spring.io/ 修改pom.xml中内容 <!-- 代码库 --> <repositories> &l…
阅读更多...
如何提高量化策略回测的效率

如何提高量化策略回测的效率

数量技术宅团队在CSDN学院推出了量化投资系列课程 欢迎有兴趣系统学习量化投资的同学&#xff0c;点击下方链接报名&#xff1a; 量化投资速成营&#xff08;入门课程&#xff09; Python股票量化投资 Python期货量化投资 Python数字货币量化投资 C语言CTP期货交易系统开…
阅读更多...
教你轻松设计圣诞节日活动的邀请函？

教你轻松设计圣诞节日活动的邀请函？

即将迎来一年一度的圣诞活动&#xff0c;商家们要如何对此次活动展开宣传呢&#xff1f;要如何制作出一张符合节日气氛的活动邀请函&#xff1f;下面小编就教你如何使用在线工具乔拓云&#xff0c;用在线邀请函模板设计活动邀请函&#xff0c;一键就能生成活动邀请函链接&#…
阅读更多...
springmvc整体运行流程

springmvc整体运行流程

请求处理的流程 1&#xff1a;浏览器发送请求送至前端控制器DispatcherServlet。 2&#xff1a;DispatcherServlet收到请求后调用HandlerMapping处理器映射器。 3&#xff1a;处理器映射器找到具体的Handler处理器&#xff0c;封装成为执行链 4&#xff1a;返回执行链给Disp…
阅读更多...
SpringBoot+MyBatis多表查询：以点餐系统的订单管理为例

SpringBoot+MyBatis多表查询：以点餐系统的订单管理为例

文章目录项目场景数据库设计POJODaoServiceTest运行结果问题及解决项目场景 SpringBoot MyBatis &#xff0c;实现点餐系统的订单查询。 参考&#xff1a;SpringBootMyBatis多表联合查询 数据库设计 通常一个订单中会包含多个菜品&#xff0c;即一条 order 里含多个 item&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023