前言

本文讲解关于动态规划思路的两道题目。

一、动态规划五步曲

1.确定状态表示（确定dp数组的含义）
2.确定状态转移方程（确定dp的递推公式）
3.确定如何初始化（初始化要保证填表正确）
4.确定遍历顺序
5.返回值

二、地下城游戏

点我直达~
在这里插入图片描述

题目分析

根据题目可知，每一个位置都对应这三种情况：
（d[i][j]由题目给出。）

1.d[i][j] < 0 ：该位置有恶魔，骑士打败恶魔会掉血。
2.d[i][j] = 0 ：该位置是一条过道，不消耗血量。
3.d[i][j] > 0 ：该位置有一个血包，吃了血包可以加血。

我们知道，到达某个位置必须保证骑士血量大于1，否则就算该位置是一个大血包，骑士也享受不到。

思路：动态规划

1.状态表示（确定dp数组的含义）
每一道dp题的第一点往往是最重要的，我们需要根据经验+题目要求来确定。
一般来说，根据经验，确定状态表示有两种：

（1）以[i,j]位置为终点，…
（2）以[i,j]位置为起点，…

写了众多dp题，大部分题型是以[i,j]位置为终点，…，所以我们先看第一种情况：

- （1）dp[i][j]表示：从起点出发，到达以[i,j]位置为终点时，所需要的最低健康值为dp[i][j].
  那么来看第二步，如何确定递推公式呢？
  请看下图：
  
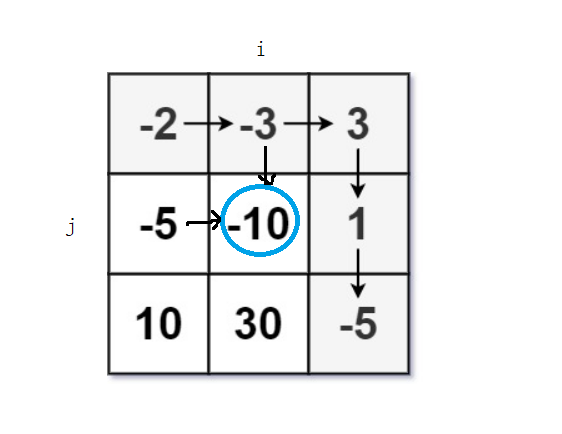
  以该图[i,j]位置为例，到达该位置一定是由上方走来或者左侧走来，所以我们需要考虑上方和左方的两种情况。
  根据题目意思，到达任意一个位置所需要的最低血量最少是1。
  所以我们不仅需要考虑当前位置，还需要考虑上方位置，左方位置，那么到达上方位置又需要进一步考虑，也就是说：到达[i,j]位置需要考虑其之前的所有的位置。并且到达[i,j]位置之后，如果未到达公主所在位置，我们仍然需要考虑后面的位置。并且初始的位置也是题目所要求我们求的，所以这个状态表示行不通。
  来看第二种。
- （2）dp[i][j]表示：从[i,j]位置出发，到达终点时，所需要的最低健康值为dp[i][j].
  这样就可以行得通了。
  我们只需要考虑它的右方和下方位置即可。
2.状态转移方程（确定递推公式）
根据状态表示，和题目描述，我们知道[i,j]位置的下一步一定是走到[i+1,j] 或者[i,j+1]位置上的。所以我们应该考虑这三者之间的关系。
我们知道，骑士到达任意一个位置，要求的最低血量必须大于等于1。
所以我们从[i,j]位置出发，走到[i+1,j] 或者[i,j+1]位置上之后，在两个位置的任意一个中，血量必须大于等于1。否则就算该位置有大血包，骑士也无法享受。
那么我们在考虑走到下一步时，应该先考虑自己位置上的值，应该+d[i][j],那么走到下一个位置的话，当前位置的最低健康点数必须大于等于下一个位置的最低健康点数，这样才能保证我们顺利走到下一个位置。
所以递推公式如下：
dp[i][j] + d[i][j] >= dp[i+1][j]或 dp[i][j] + d[i][j] >= dp[i][j+1]
进行一下移项，得：
dp[i][j] >= dp[i+1][j] - d[i][j]或 dp[i][j] >= dp[i][j+1] - d[i][j]
由于要求最小的健康值，则当等于号成立时，就是最低的健康点数了：
dp[i][j] = min(dp[i][j+1],dp[i+1][j]) - d[i][j]

但是有一个需要注意的点，当d[i][j]是一个非常大的数时，可能会导致减了d[i][j]之后，dp[i][j]是一个非正整数了，则表示骑士走到[i,j]位置是挂了的状态，并且还能吃了当前位置的血包顺利走到下一个位置，这显然是不符合逻辑的。
所以当dp[i,j]是一个非正整数时，所要求能通过当前位置的最低健康值就是1。
即dp[i][j] = max(1,dp[i][j])

代码如下：

dp[i][j] = min(dp[i-1][j],dp[i][j-1]) - d[i][j];
dp[i][j] = max(1,dp[i][j]);

3.确定如何进行初始化
上面分析了那么久，我们大概知道当骑士从公主所在位置出发到达公主所在位置时，即：

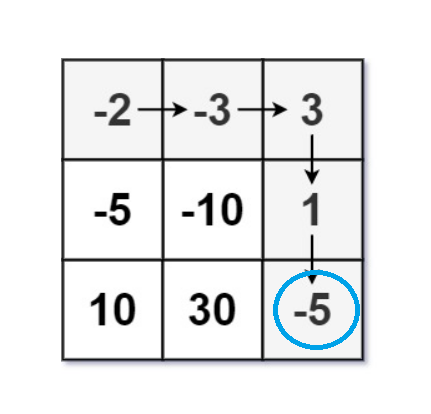
需要知道[i+1,j]位置和[i,j+1]位置。
所以我们在初始化时，需要多开一行一列的虚拟空间，来更好地进行初始化。具体如下图：

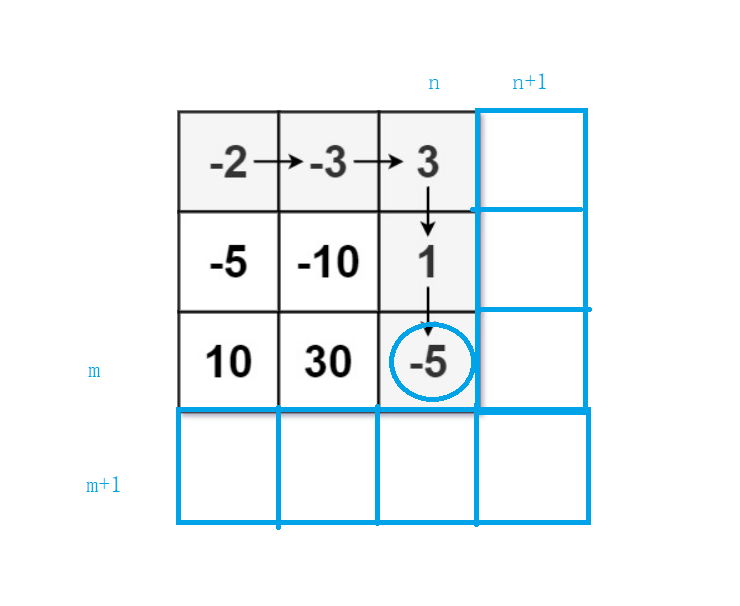
此时我们需要注意的点是：
虚拟空间的初始化必须保证不能影响正常结果。
在之前写的dp题目中，虚拟空间还需要注意第二点：
下标的映射关系，在这道题中，不需要注意，因为虚拟的空间并没有影响下标。
所以dp[m][n+1] 和dp[m+1][n]位置应该初始化成1，因为走到那个位置，最低健康值必须大于等于1，所以最小值为1。则其他位置根据以往经验，要保证不影响其他值，需要初始化成正无穷大。

4.遍历顺序
应该从下往上遍历，每行从右往左遍历。
5.返回值
返回dp[0][0]的值。

具体代码如下

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& d) 
    {
        //1.确定dp数组的含义
        //dp[i,j]表示:以[i,j]位置为起点，到达终点位置所需要的最小健康点数为dp[i][j]
        
        //2.确定递推公式    
        //dp[i][j] = min(dp[i+1][j],dp[i][j+1]) - d[i][j]
        //但是有可能算出来是非正整数，意味着走到这个位置已经是死了的状态，不符合题目要求。所以如果是非正整数的话，必须最小健康点数为1.
        //dp[i][j] = max(1,dp[i][j]);   
        //3.确定如何初始化
        //由于dp数组的含义是以[i,j]位置为起点的，所以我们必须从终点位置开始初始化，那么应该多开一行一列的虚拟空间来更好地初始化。
        //注意：1.虚拟空间的初始化不能影响结果。
        //这道题不同于之前的题，这里无需再注意下标的映射关系
        //4.遍历顺序(从下到上遍历，每行从右往左遍历)
        //5.返回值
        //dp[0][0]
        int m = d.size();
        int n = d[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
        dp[m-1][n] = dp[m][n-1] = 1;

        for(int i = m-1;i>=0;i--)
        {
            for(int j = n-1;j>=0;j--)
            {
                dp[i][j] = min(dp[i][j+1],dp[i+1][j]) - d[i][j];
                //如果dp[i][j] <=0 ，则必须保证到[i,j]位置最低血量为1
                dp[i][j] = max(1,dp[i][j]);
            }
        }

        return dp[0][0];
        //时空复杂度O(m*n)
    }
};