❓ 463. 岛屿的周长

难度：简单

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地，grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 1：

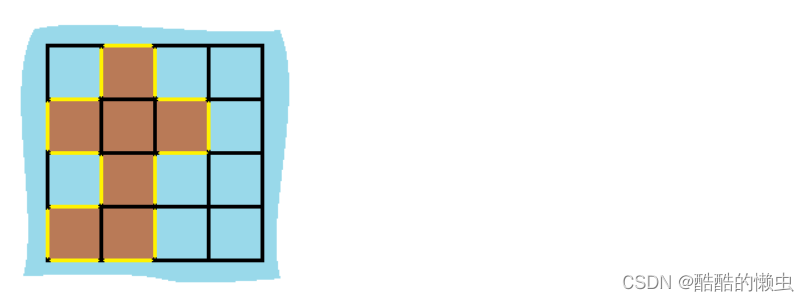
输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

示例 2：

输入：grid = [[1]]
输出：4

示例 3：

输入：grid = [[1,0]]
输出：4

提示：

• row == grid.length
• col == grid[i].length
• 1 <= row, col <= 100
• grid[i][j] 为 0 或 1

💡思路：模拟

岛屿问题最容易让人想到 BFS 或者 DFS，但是这道题还真的没有必要，别把简单问题搞复杂了。

法一：

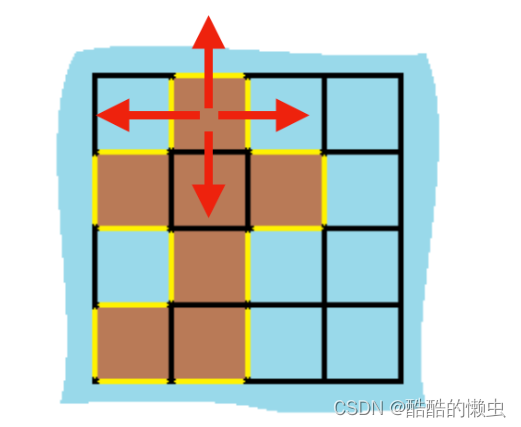
遍历所有格子，判断每个格子的四周：

• 如果直接和水域相连，则周长 +1;
• 如果和陆地相连，周长不变。
  

法二：

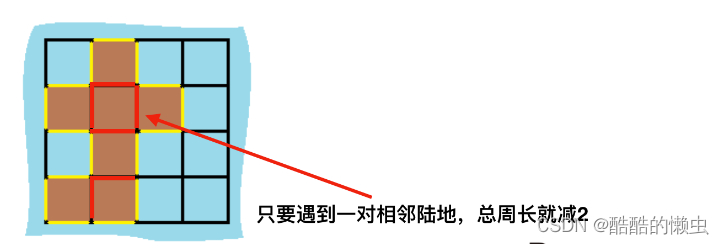
计算出总的岛屿数量，因为有一对相邻两个陆地，边的总数就减2，那么在计算出相邻岛屿的数量就可以了。

🍁代码：(C++、Java)

法一：
C++

class Solution {
public:
    int islandPerimeter(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int ans = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 0) continue;
                if(j == 0 || (j > 0 && grid[i][j - 1] == 0)) ans++;//左
                if(i == 0 || (i > 0 && grid[i - 1][j] == 0)) ans++;//上
                if(j == n - 1 || (j < n - 1 && grid[i][j + 1] == 0)) ans++;//右
                if(i == m - 1 || (i < m - 1 && grid[i + 1][j] == 0)) ans++;//下
            }
        }
        return ans;
    }
};

Java

class Solution {
    public int islandPerimeter(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int ans = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 0) continue;
                if(j == 0 || (j > 0 && grid[i][j - 1] == 0)) ans++;//左
                if(i == 0 || (i > 0 && grid[i - 1][j] == 0)) ans++;//上
                if(j == n - 1 || (j < n - 1 && grid[i][j + 1] == 0)) ans++;//右
                if(i == m - 1 || (i < m - 1 && grid[i + 1][j] == 0)) ans++;//下
            }
        }
        return ans;
    }
}

法二：
C++

class Solution {
public:
    int islandPerimeter(vector<vector<int>>& grid) {
        int count = 0, cover = 0;
        int ans = 0;
        for(int i = 0; i < grid.size(); i++){
            for(int j = 0; j < grid[0].size(); j++){
                if(grid[i][j] == 0) continue;
                count++;
                // 统计上边相邻陆地
                if(i - 1 >= 0 && grid[i - 1][j] == 1) cover++;
                // 统计左边相邻陆地
                if(j - 1 >= 0 && grid[i][j - 1] == 1) cover++;
                // 为什么没统计下边和右边？ 因为避免重复计算
            }
        }
        return count * 4 - cover * 2;
    }
};

Java

class Solution {
    public int islandPerimeter(int[][] grid) {
        int count = 0, cover = 0;
        int ans = 0;
        for(int i = 0; i < grid.length; i++){
            for(int j = 0; j < grid[0].length; j++){
                if(grid[i][j] == 0) continue;
                count++;
                // 统计上边相邻陆地
                if(i - 1 >= 0 && grid[i - 1][j] == 1) cover++;
                // 统计左边相邻陆地
                if(j - 1 >= 0 && grid[i][j - 1] == 1) cover++;
                // 为什么没统计下边和右边？ 因为避免重复计算
            }
        }
        return count * 4 - cover * 2;
    }
}

🚀 运行结果：

🕔 复杂度分析：

• 时间复杂度：$O(mn)$，其中 m 为网格的高度， n 为网格的宽度。我们需要遍历每个格子，每个格子要看其周围 4个格子是否为岛屿，因此总时间复杂度为 $O(4nm)=O(nm)$。
• 空间复杂度：$O(1)$，只需要常数空间存放若干变量。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我LeetCode主页 / CSDN—力扣专栏，每日更新！

注： 如有不足，欢迎指正！