这里写目录标题
- 一、Simulink 系统仿真实例
- 1. 方法一
- 2. 方法二
- 3. 方法三
- 二、S 函数的设计与应用
- 1. 用 MATLAB 语言编写 S 函数
- 1.1 主程序
- 1.2 子程序
- 2. S 函数的应用
一、Simulink 系统仿真实例
- 下面的应用实例我们将分别采用不同建模方法为系统建模并仿真。
- 例如,有初始状态为 0 的二阶微分方程 x ′ ′ + 0.2 x ′ + 0.4 x = 0.2 u ( t ) x''+0.2x'+0.4x=0.2u(t) x′′+0.2x′+0.4x=0.2u(t),其中 u ( t ) u(t) u(t) 是单位阶跃函数,对此我们尝试建立系统模型并仿真 。
1. 方法一
- 我们利用 Integrator(积分器)模块直接构造求解微分方程的模型。
- 我们将原微分方程改写为 x ′ ′ = 0.2 u ( t ) − 0.2 x ′ − 0.4 x x''=0.2u(t)-0.2x'-0.4x x′′=0.2u(t)−0.2x′−0.4x
- x ′ ′ x'' x′′ 经积分作用得 x ‘ x‘ x‘, x ′ x' x′ 再经积分模块作用就得 x x x,而 x ′ x' x′ 和 x x x 经代数运算又产生 x ′ ′ x'' x′′,据此可以建立系统模型并仿真。步骤如下。
- (1) 利用 Simulink 模块库中的基本模块不难建立如下图所示的系统模型。
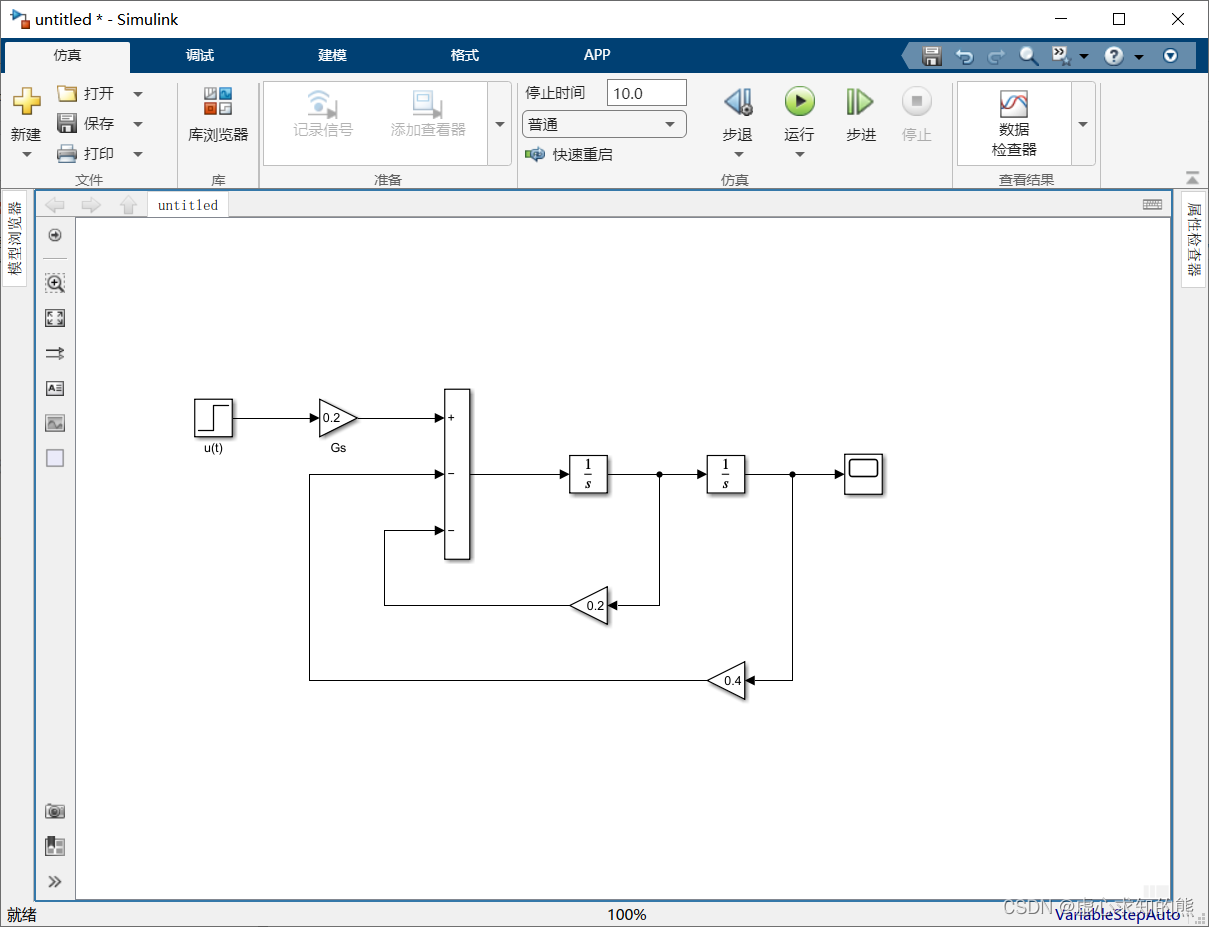
- 模型中各个模块说明如下。
- ① u(t) 输入模块:它的 Step time 被设置为 0,模块名称由原来的 Step 改为 u(t)。
- ② Gs 增益模块:增益参数 Gain 设置为 0.2。
- ③ Add 求和模块:其图标形状 Icon shape 设置为 rectangular,符号列表 List of signs 设置为 ±-。
- ④ Integrator 积分模块:参数不需要改变。
- ⑤ G1 和 G2 反馈增益模块:增益参数分别设置为 0.4 和 0.2,它们的方向翻转可借助快捷菜单中的 Rotate & Flip ⟶ \longrightarrow ⟶Flip Block 命令或模型编辑窗口的 Diagram ⟶ \longrightarrow ⟶Rotate & Flip ⟶ \longrightarrow ⟶Flip Block 命令实现。
- (2) 设置系统仿真参数。打开 Configuration Parameters 窗口,把仿真的终止时间设置为 20s。
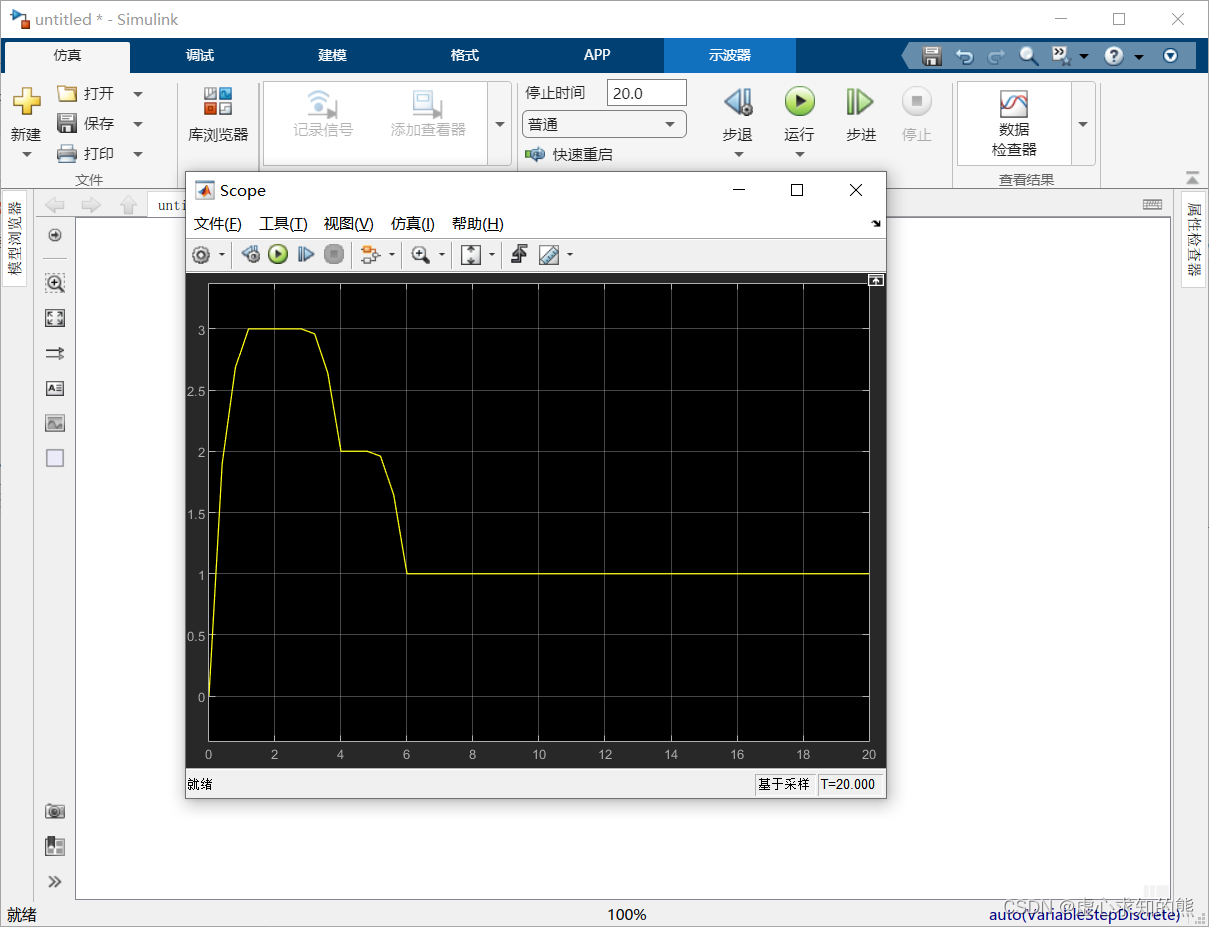
- (3) 仿真操作。双击示波器图标,打开示波器窗口。单击模型编辑窗口工具栏中的 Run 按钮,就可在示波器窗口中看到仿真结果的变化曲线,如下图所示。

2. 方法二
- 利用传递函数模块(Transfer Fcn)建模。
- 对方程 x ′ ′ + 0.2 x ′ + 0.4 x = 0.2 u ( t ) x''+0.2x'+0.4x=0.2u(t) x′′+0.2x′+0.4x=0.2u(t) 两边取 Laplace 变换,得 s 2 X ( s ) + 0.2 s X ( s ) + 0.4 X ( s ) = 0.2 U ( s ) s^{2}X(s)+0.2sX(s)+0.4X(s)=0.2U(s) s2X(s)+0.2sX(s)+0.4X(s)=0.2U(s)
- 经整理得传递函数 G ( s ) = X ( s ) U ( s ) = 0.2 s 2 + 0.2 s + 0.4 G(s)=\frac{X(s)}{U(s)}=\frac{0.2}{s^{2}+0.2s+0.4} G(s)=U(s)X(s)=s2+0.2s+0.40.2
- 在 Continuous 模块库中有标准的传递函数(Transfer Fcn)模块可供调用,于是,就可以构建求解微分方程的模型并仿真。根据系统传递函数构建如下图所示的仿真模型。
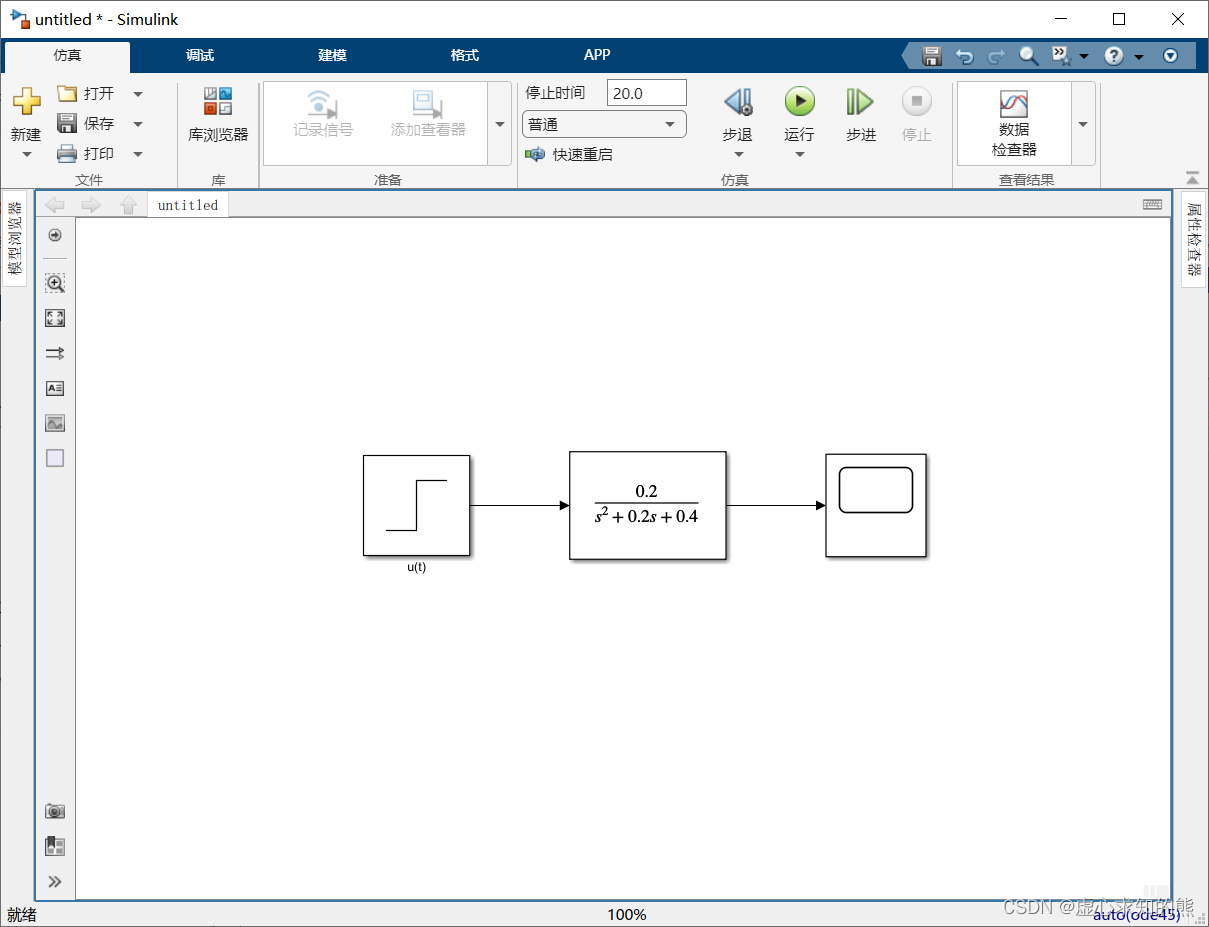
- 模型中各个模块说明如下。
- (1) u(t) 模块:设置 Step time 为 0。
- (2) G(S) 模块:双击 Transfer Fcn 模块,打开参数设置对话框,在 Numerator coefficients 文本框中输入传递函数的分子多项式系数 [0.2],在 Denominator coefficients 文本框中输入传递函数的分母多项式的系数 [1,0.2,0.4],如下图所示。
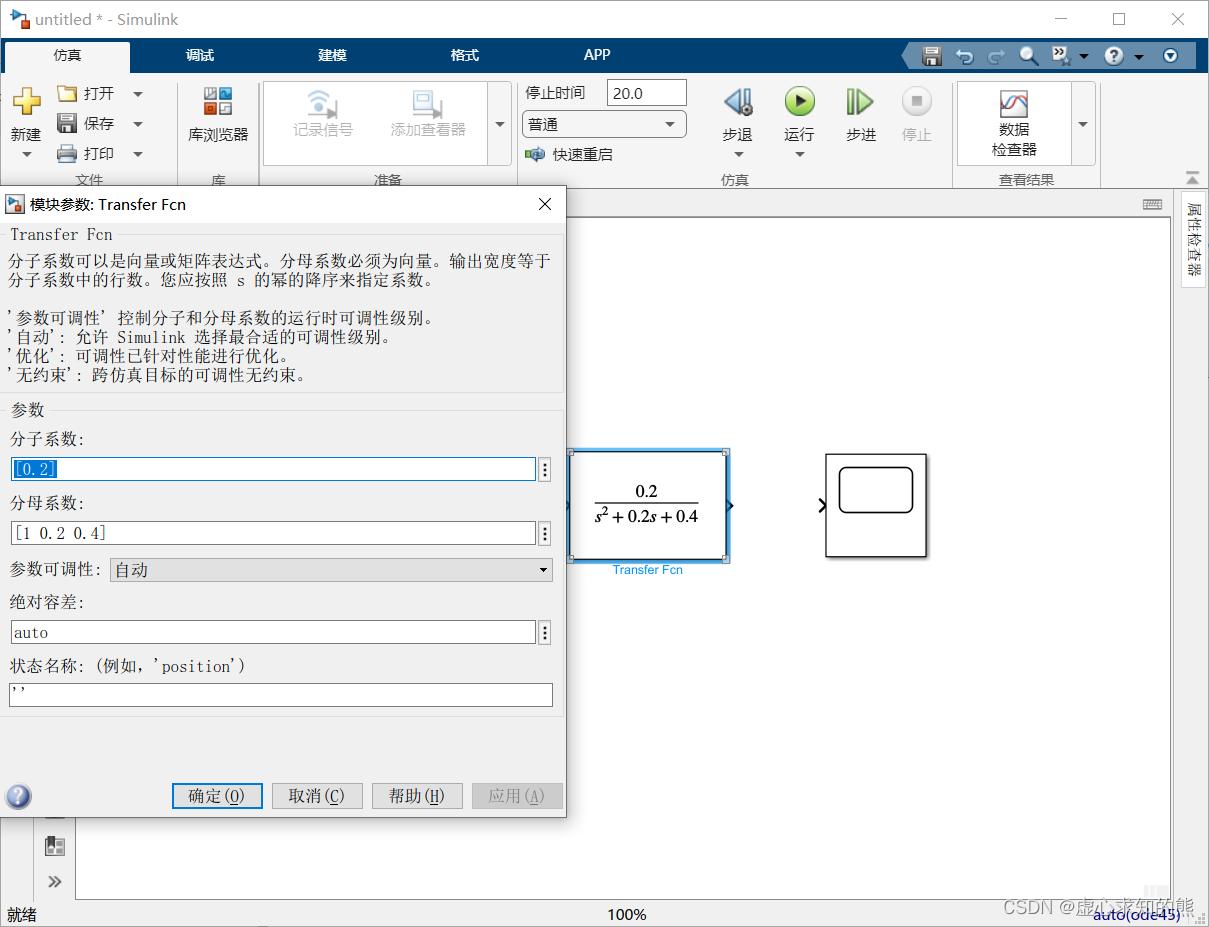
- 以后的操作与方法 1 相同。
3. 方法三
- 利用状态方程模块(State-Space)建模。
- 若令 x 1 = x x_{1}=x x1=x, x 2 = x ′ x_{2}=x' x2=x′,那么微分方程 x ′ ′ + 0.2 x ′ + 0.4 x = 0.2 u ( t ) x''+0.2x'+0.4x=0.2u(t) x′′+0.2x′+0.4x=0.2u(t) 可写成 x ′ = [ x 1 ′ x 2 ′ ] = [ 0 1 − 0.4 − 0.2 ] [ x 1 x 2 ] + [ 0 0.2 ] u ( t ) x'=\begin{bmatrix}x^{'}_{1} \\x^{'}_{2} \end{bmatrix}=\begin{bmatrix} 0&1 \\ -0.4&-0.2 \end{bmatrix}\begin{bmatrix}x_{1} \\x_{2} \end{bmatrix}+\begin{bmatrix}0 \\0.2 \end{bmatrix}u(t) x′=[x1′x2′]=[0−0.41−0.2][x1x2]+[00.2]u(t)
- 写成状态方程为 { x ′ = A x + B u y = C x + D u \left\{\begin{matrix}x^{'}=Ax+Bu \\y=Cx+Du \end{matrix}\right. {x′=Ax+Buy=Cx+Du
- 式中, A = [ 0 1 − 0.4 − 0.2 ] A=\begin{bmatrix} 0&1 \\ -0.4 &-0.2 \end{bmatrix} A=[0−0.41−0.2], B = [ 0 − 0.2 ] B=\begin{bmatrix} 0 \\ -0.2 \end{bmatrix} B=[0−0.2], C = [ 1 0 ] C=\begin{bmatrix} 1&0 \end{bmatrix} C=[10], D = 0 D=0 D=0。
- 在 Continuous 模块库中有标准的状态方程(State-Space)模块可供调用,于是,就可以构建求解微分方程的模型并仿真。根据系统状态方程构建如下图所示的仿真模型。
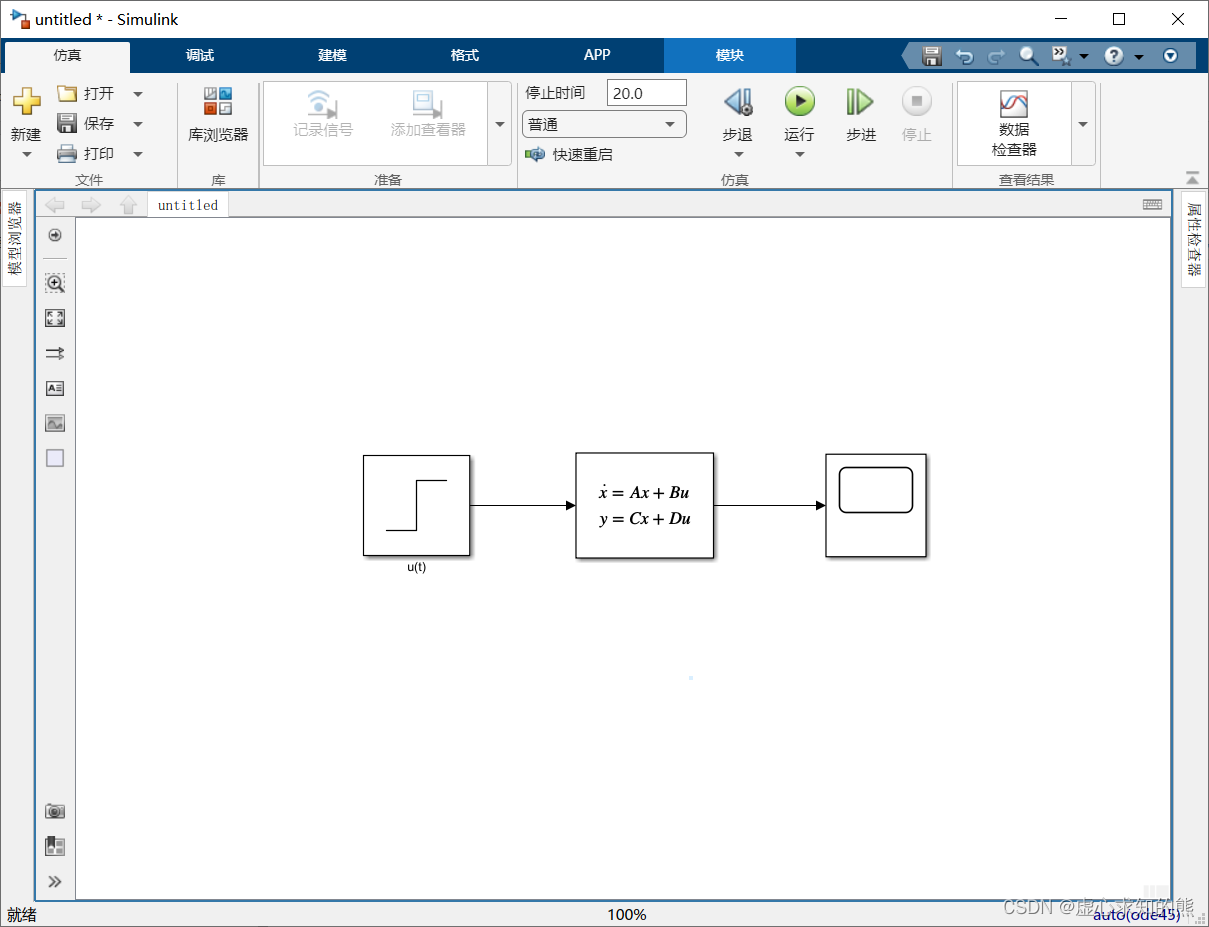
- 模型中各个模块说明如下:
- (1) u(t) 输入模块:它的 Step time 被设置为 0。
- (2) State-Space 模块:A、B、C、D 各文本框中依次输入 [0,1;-0.4,-0.2]、[0;0.2]、[1,0] 和 0,如下图所示。
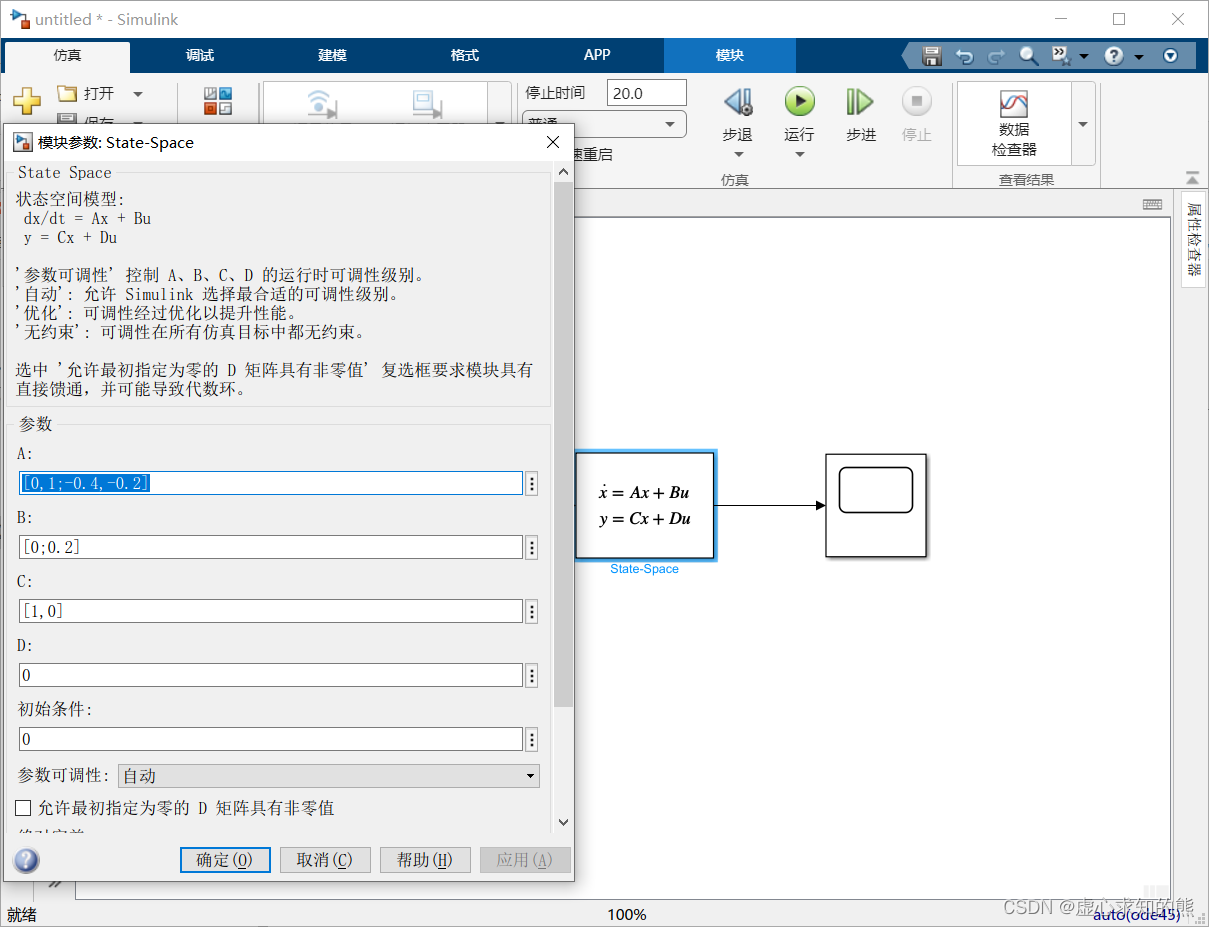
- 后面的操作与方法 1 相同。
二、S 函数的设计与应用
- S 函数用于开发新的 Simulink 通用功能模块,是一种对模块库进行扩展的工具。S 函数可以采用 MATLAB 语言以及 C、C++、FORTRAN 等语言编写。
- 在 S 函数中使用文本方式输入公式、方程,非常适合复杂动态系统的数学描述,并且在仿真过程中可以对仿真进行更精确的控制。
- S 函数称为系统函数(System Function),采用非图形化的方式描述功能模块。
- MATLAB 语言编写的 S 函数可以充分利用 MATLAB 所提供的丰富资源,方便地调用各种工具箱函数和图形函数使用;
- C 语言编写的 S 函数可以实现对操作系统的访问,如实现与其他进程的通信和同步等。
- 非 MATLAB 语言编写的 S 函数需要用编译器生成 MEX 文件。
1. 用 MATLAB 语言编写 S 函数
- S 函数有固定的程序格式,可以从 Simulink 提供的 S 函数模板程序开始构建自己的 S 函数。
1.1 主程序
- S 函数主程序的引导语句如下:
function [sys,x0,str,ts]=fname(t,x,u,flag)
- 其中,fname 是 S 函数的函数名,t、x、u、flag 分别为仿真时间、状态向量、输入向量和子程序调用标志。 flag 控制在仿真的各阶段调用 S 函数的哪一个子程序,其含义和有关信息如下表所示。
| 取值 | 功能 | 调用函数名 | 返回参数 |
|---|---|---|---|
| 0 | 初始化 | mdllnitializeSizes | sys 为初始化参数,x0、str、ts 如定义 |
| 1 | 计算连续状态变量的导数 | mdlDerivatives | sys 返回连续状态 |
| 2 | 计算离散状态变量的更新 | mdIUpdate | sys 返回离散状态 |
| 3 | 计算输出信号 | mdlOutputs | sys 返回系统输出 |
| 4 | 计算下一个采样时刻 | mdlGetTimeOfNextVarHit | sys 返回下一步仿真的时间 |
| 9 | 结束仿真任务 | mdlTerminate | 无 |
- Simulink 每次调用 S 函数时,必须给出这 4 个参数。sys、x0、str 和 ts 是 S 函数的返回参数。
- sys 是一个返回参数的通用符号,它得到何种参数取决于 flag 值。例如,flag=3 时,sys 得到的是 S 函数的输出向量值。
- x0 是初始状态值,如果系统中没有状态变量,x0 将得到一个空阵。
- str 仅用于系统模型同 S 函数 API(应用程序编程接口)的一致性校验。对于 M 文件 S 函数,它将被置成一个空阵。
- ts 是一个两列矩阵,一列是 S 函数中各状态变量的采样周期,另一列是相应的采样时间的偏移量。采样周期按递增顺序排列,ts 中的一行对应一个采样周期。对于连续系统,采样周期和偏移量都应置成 0。如果取采样周期为 -1,则将继承输入信号的采样周期。
- 此外,在主程序输入参数中还可以包括用户自定义参数表: pl,p2,…,pn,这也就是希望赋给 S 函数的可选变量,其值通过相应 S 函数的参数对话框设置,也可以在命令行窗口赋值。
- 于是 S 函数主程序的引导语句可以写成
function [sys,x0,str,ts]=fname(t,x,u,flag,pl,p2,…,pn)
- 主程序采用 switch-case 语句,引导 Simulink 到正确的子程序。
1.2 子程序
- M 文件 S 函数共有 6 个子程序,供 Simulink 在仿真的不同阶段调用,这些子程序的前缀为 mdl。
- 每一次调用 S 函数时,都要给出一个 flag 值,实际执行 S 函数中与该 flag 值对应的那个子程序。
- Simulink 在仿真的不同阶段,需要调用 S 函数中不同的子程序。
- (1) 初始化子程序 mdlInitializeSizes。子程序 mdlInitializeSizes 定义 S 函数参数,如采样时间、输入量、输出量、状态变量的个数以及其他特征。
- 为了向 Simulink 提供这些信息,在子程序 mdlInitializeSizes 的开始处,应调用 simsizes 函数,这个函数返回一个 sizes 结构,结构的成员 sizes.NumContStates、sizes.NumDiscStates、sizes.NumOutputs 和 sizes.NumInputs 分别表示连续状态变量的个数、离散状态变量的个数、输出的个数和输入的个数。这 4 个值可以置为 -1,使其大小动态改变。
- 成员 sizes.DirFeedthrough 是直通标志,即输入信号是否直接在输出端出现的标志,是否设定为直通,取决于输出是否为输入的函数,或者取样时间是否为输入的函数。1 表示 yes,0 表示 no。成员 sizes.NumSampleTimes 是模块采样周期的个数,一般取 1。
- 按照要求设置好的结构 sizes 用 sys=simsizes(sizes) 语句赋给 sys 参数。除了 sys 外,还应该设置系统的初始状态变量 x0、说明变量 str 和采样周期变量 ts。
- (2) 其他子程序。状态的动态更新使用 mdlDerivatives 和 mdIUpdate 两个子程序,前者用于连续状态的更新,后者用于离散状态的更新。这些函数的输出值,即相应的状态,均由 sys 变量返回。
- 对于同时含有连续状态和离散状态的混合系统,则需要同时写出这两个函数来分别描述连续状态和离散状态。
- 模块输出信号的计算使用 mdlOutputs 子程序,系统的输出仍由 sys变量返回。
- 一般应用中很少使用 flag 为 4 和 9 的情况,mdlGetTimeOfNextVarHit 和 mdlTerminate 两个子程序较少使用。
2. S 函数的应用
- 下面来看两个简单的 M 文件 S 函数例子。
- 例如,我们采用 S 函数实现 y = n x y=nx y=nx,即把一个输入信号放大 n n n 倍。
- (1) 利用 MATLAB 语言编写 S 函数,程序如下。
%****************************************
%S函数timesn.m,其输出是输入的n倍
%****************************************
function [sys,x0,str,ts]=timesn(t,x,u,flag,n)
switch flag
case 0
[sys,x0,str,ts]=mdlInitializeSizes; %初始化
case 3
sys=mdloutputs(t,x,u,n); %计算输出量
case {1,2,4,9}
sys=[];
otherwise %出错处理
error(num2str(flag));
end
%****************************************
%mdlInitializesizes:当flag为0时进行整个系统的初始化
%******************** ********************
function [sys,x0,str,ts]=mdlInitializeSizes()
%调用函数simsizes以创建结构sizes
sizes=simsizes;
%用初始化信息填充结构sizes
sizes.NumContStates=0; %无连续状态
sizes.NumDiscStates=0; %无离散状态
sizes.NumOutputs=1; %有一个输出量
sizes.NumInputs=1; %有一个输入信号
sizes.DirFeedthrough=1; %输出量中含有输入量
sizes.NumSampleTimes=1; %单个采样周期
%根据上面的设置设定系统初始化参数
sys=simsizes(sizes);
%给其他返回参数赋值
x0=[]; %设置初始状态为零状态
str=[]; %将str变量设置为空字符串
ts=[-1,0]; %假定继承输入信号的采样周期
%初始化子程序结束
%****************************************
% mdlOutputs:当flag值为3时,计算输出量
%****************************************
function sys=mdloutputs(t,x,u,n)
sys=n*u;
%输出量计算子程序结束
- 将该程序以文件名 timesn.m 存盘。编好 S 函数后,就可以对该模块进行封装和测试了。
- (2) 模块的封装与测试。
- ① 建立 S-Function 模块和编写的S函数文件之间的联系。新建一个模型,向模型编辑窗口中添加 User-Defined Functions 子模块库中的 S-Function 模块、Sine Wave 模块和 Scope 模块,构建如下图所示的仿真模型。
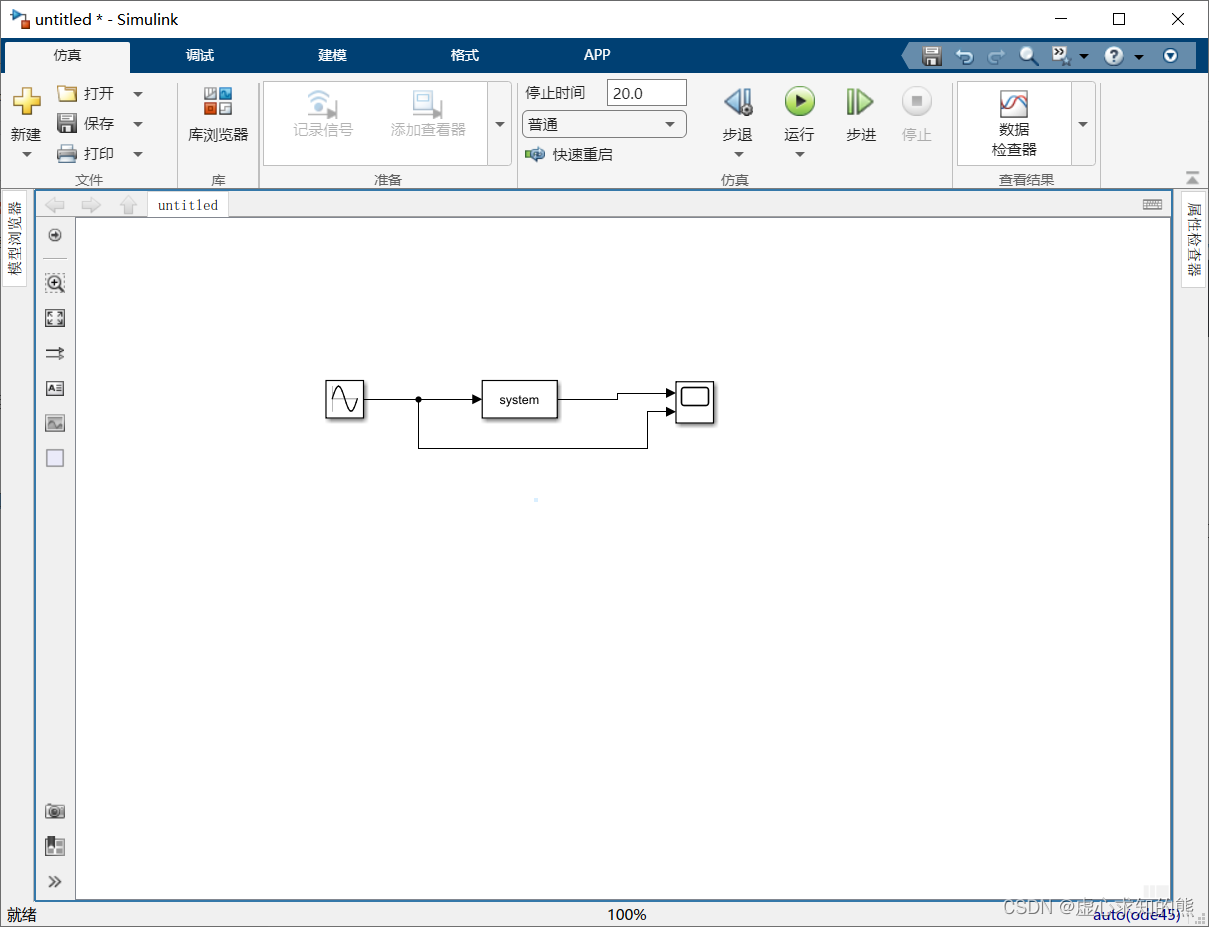
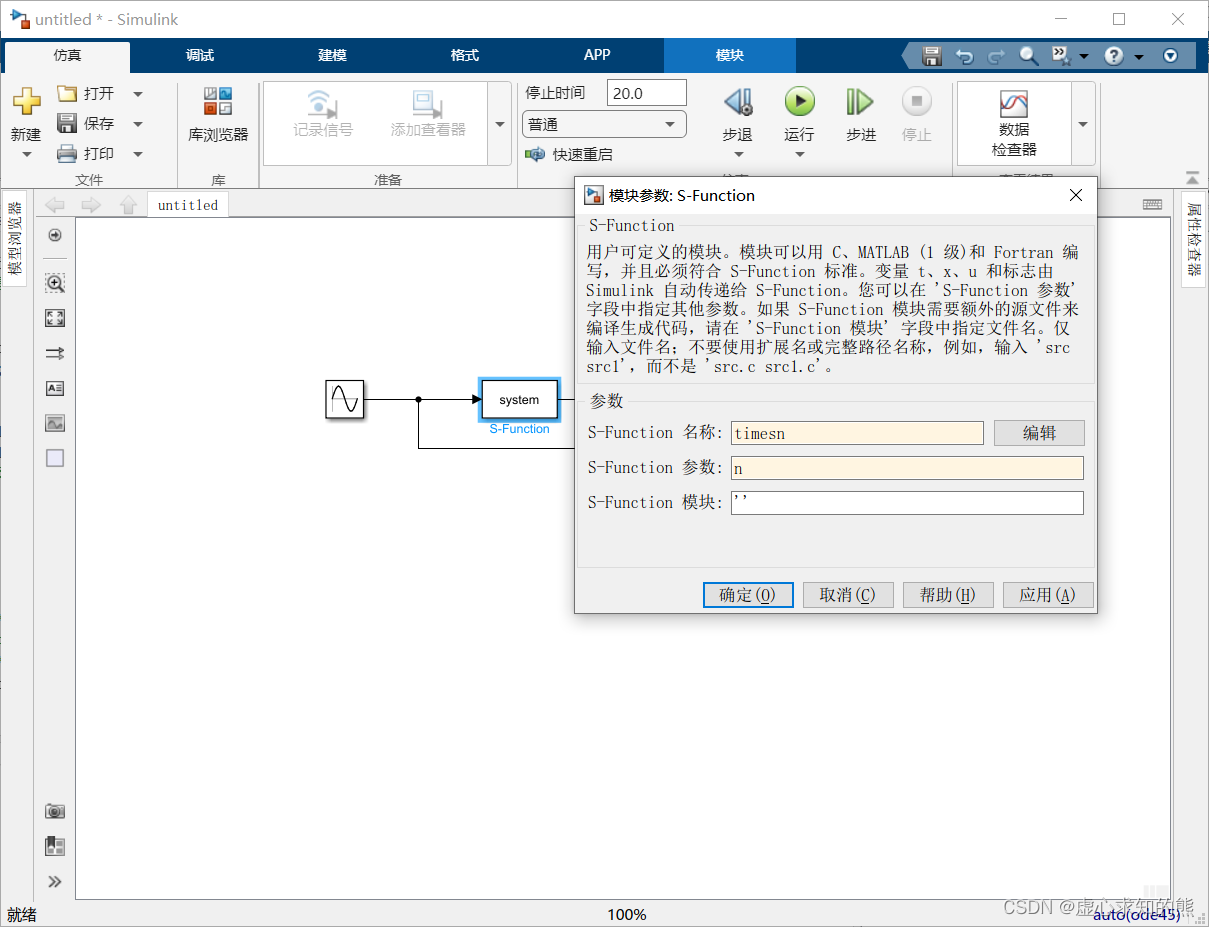
- 在模型编辑窗口中双击 S-Function 模块打开如下图所示的参数对话框,在 S-functionname 编辑框中输入 S 函数名 timesn 在 S-function parameters 编辑框中输入外部参数 n。
- n 可以在 MATLAB 工作空间中用命令定义。如果有多个外部参数,参数之间用逗号分隔。
- ② 模型封装。其具体操作与子系统的封装类似。在模型编辑窗口选中 S-Function 模块,再选择 Diagram ⟶ \longrightarrow ⟶Mask ⟶ \longrightarrow ⟶Create Mask 命令,或按 Ctrl+M 键,打开封装编辑器,选择 Parameters & Dialog 选项卡,在左侧控件工具箱中单击 Edit 工具,往中间的 Dialog box 区域的控件列表中添加编辑框控件 #1,选中该控件后,在右侧的 Property editor 区域中,在 Name 栏输入 n,Prompt 栏输入 “放大倍数”,勾选 Evaluate 复选框,具体如下图所示。
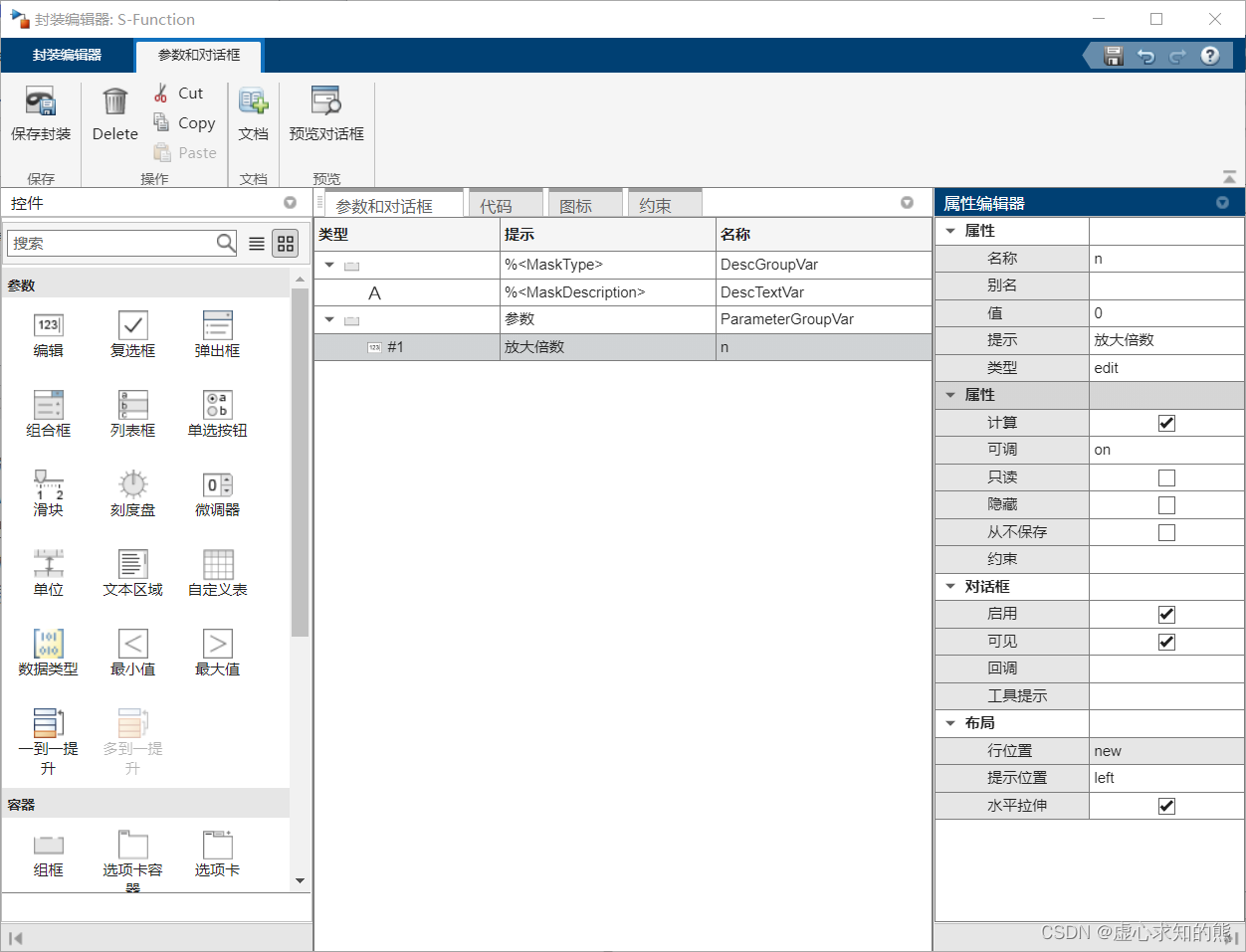 - 设置完成后单击 OK 按钮。S 函数模块被封装后,双击它,则得到如下图所示的模块参数对话框。
- 设置完成后单击 OK 按钮。S 函数模块被封装后,双击它,则得到如下图所示的模块参数对话框。
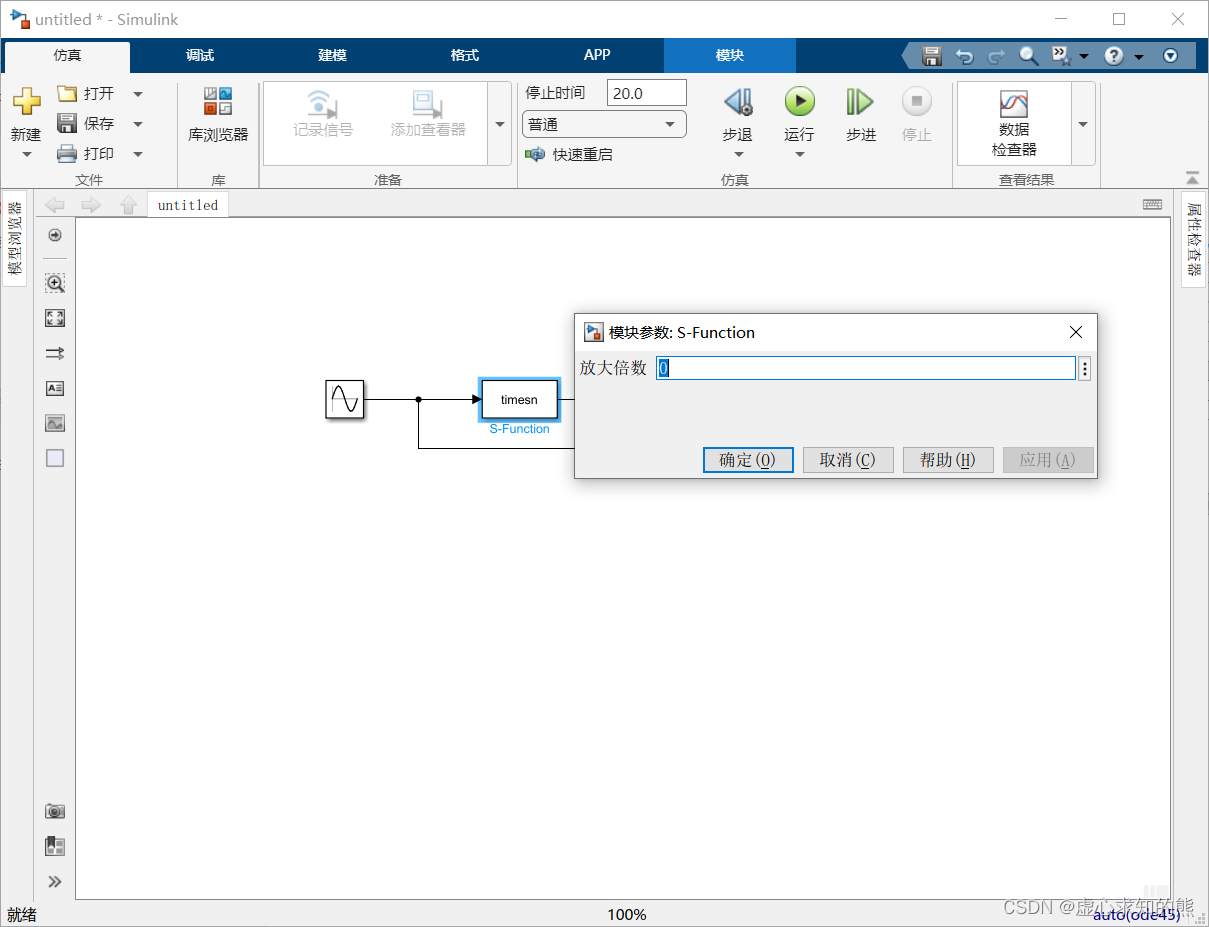
- 当输入 n 的值为 10 时,得到的仿真结果如下图所示。
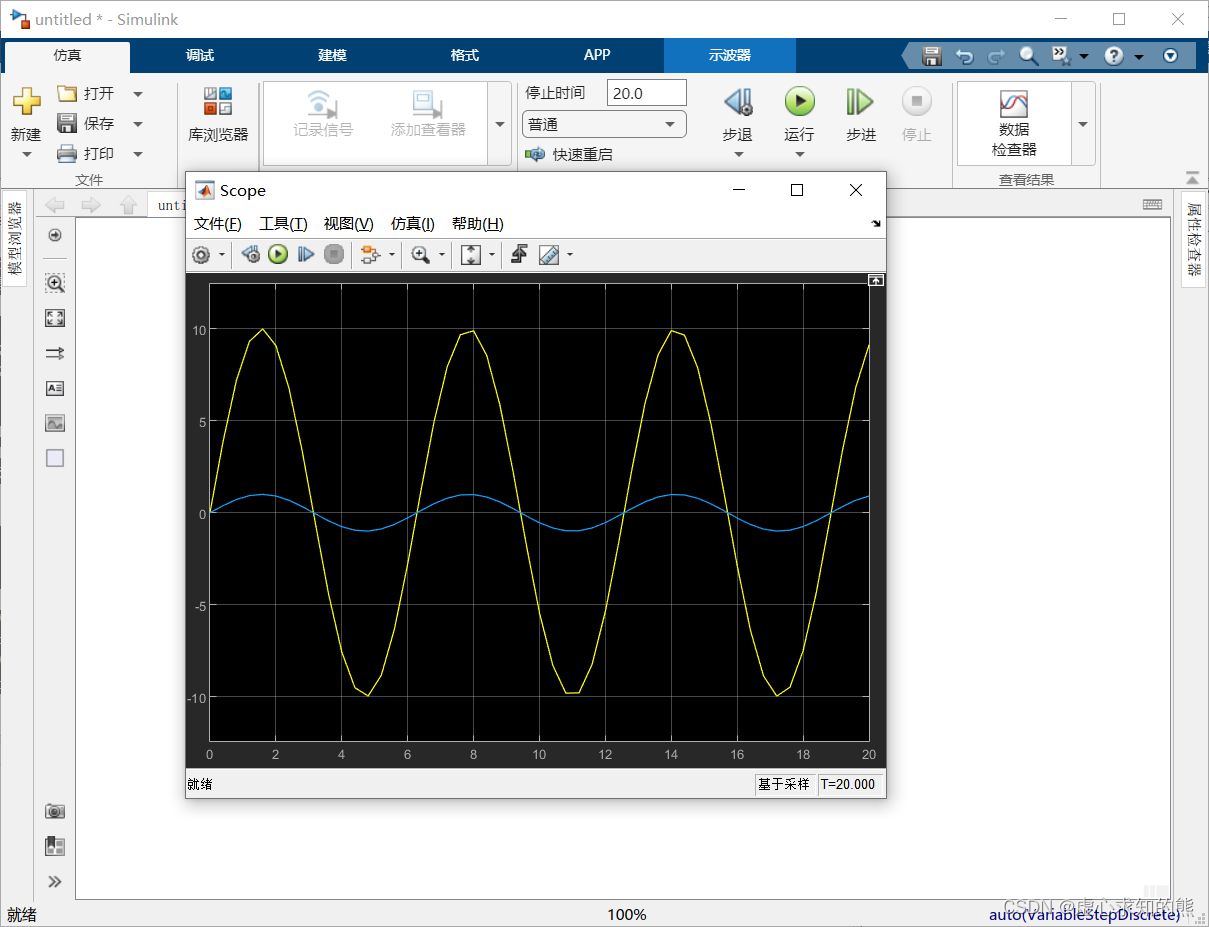
- 例如,我们采用 S 函数构造非线性分段函数 y = { 3 x x < 1 3 1 ≤ x < 3 3 − ( x − 3 ) 2 3 ≤ x < 4 2 4 ≤ x < 5 2 − ( x − 5 ) 2 5 ≤ x < 6 1 x ≥ 6 y=\left\{\begin{matrix} 3\sqrt{x}& x< 1\\ 3 & 1\le x< 3\\ 3-(x-3)^{2} &3\le x< 4 \\ 2 & 4\le x< 5\\ 2-(x-5)^{2} & 5\le x< 6\\ 1 &x\ge 6 \end{matrix}\right. y=⎩ ⎨ ⎧3x33−(x−3)222−(x−5)21x<11≤x<33≤x<44≤x<55≤x<6x≥6。
- (1) 利用 MTALAB 语言编写 S 函数,程序如下:
function [sys,x0,str,ts]=sfunction(t,x, u,flag)
switch flag
case 0
[sys,x0,str,ts]=mdlInitializeSizes;
case 3
sys=mdlOutputs(t,x,u);
case {1,2,4,9}
sys=[];
otherwise
error(['Unhandled flag=',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes=simsizes;
sizes.NumContStates=0;
sizes.NumDiscStates=0;
sizes.NumOutputs=1;
sizes.NumInputs=1;
sizes.DirFeedthrough=1;
sizes.NumSampleTimes=1;
sys=simsizes(sizes);
x0=[];
str=[];
ts=[0,0];
function sys=mdlOutputs(t,x,u)
if u<1
sys=3*sqrt(u);
elseif u>=1&&u<3
sys=3;
elseif u>=3&&u<4
sys=3-(u-3)^2;
elseif u>=4&&u<5
sys=2;
elseif u>=5&&u<6
sys=2-(u-5)^2;
else
sys=1;
end
- 将该程序以文件名 sfunction.m 存盘。
- (2) 模块的测试。向模型编辑窗口中添加 S-Function 模块,并在其参数设置对话框中输入 M 文件名 sfunction,构建如下图所示的仿真模型。
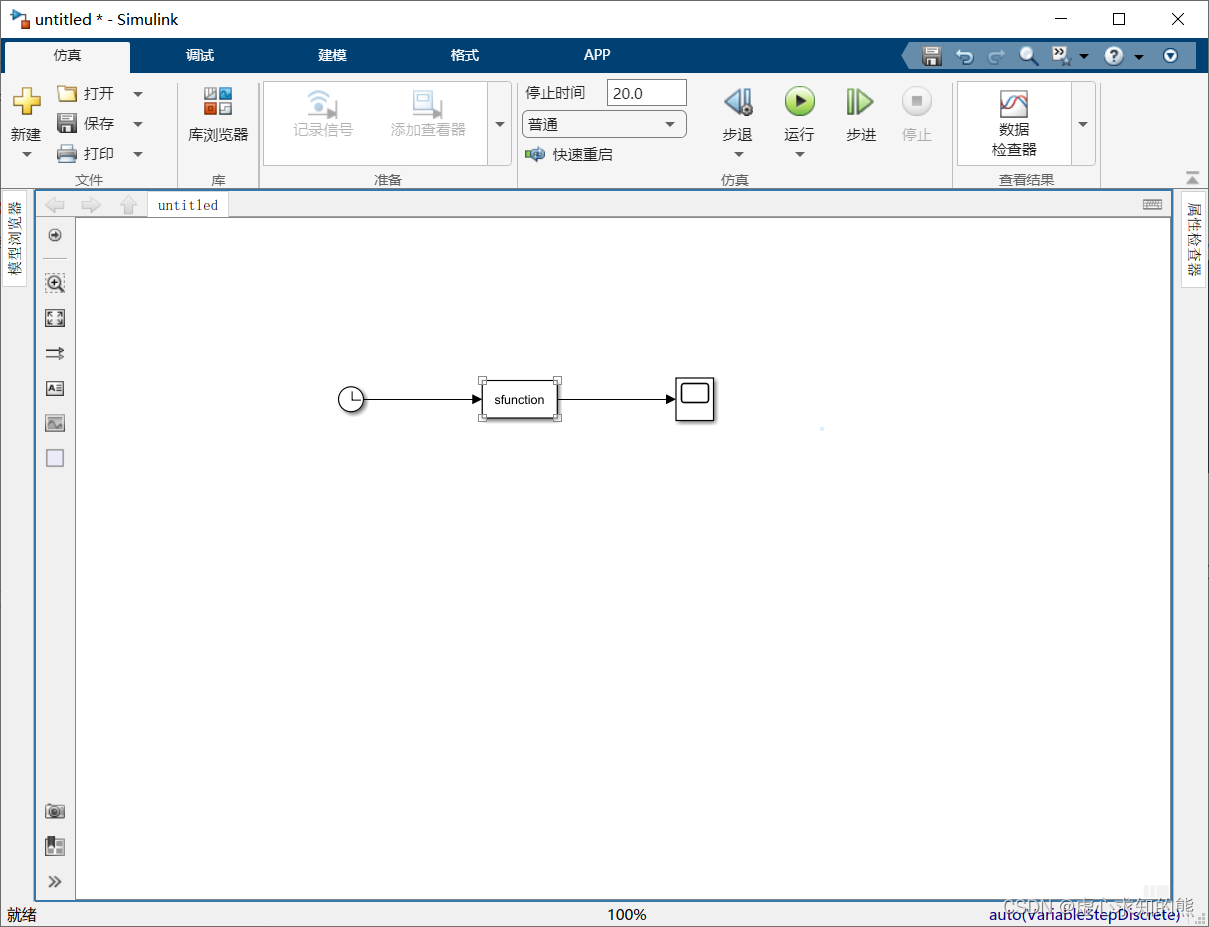
- 运行即可得到如下图所示的仿真结果。