最小生成树问题,常用于将所有顶点连通的最大最小代价。比如十个城市去修路,不同成熟时之间修路的代价不同,让你找一个方案可以满足每个城市之间互相连通并且代价最小。
解决这个问题有两个算法,Prim算法和Kruskal算法。不同的是,前者每次优先连通顶点所需代价最小的顶点,而后者是优先代价最小的边,然后去判断是否形成环。
Prim算法
该算法和Dijkstra算法差别很小。可以理解为在Dijkstra算法上稍微进行修改。本质上就是找到已连接的顶点与未连接的顶点之间最小的边,然后连接其对应的点。
例:黑色代表已经连接的顶点,红色表示未连接的顶点,观察可知黑色顶点与红色顶点之间有三条边,最小代价的是3,那就把6这个顶点连上去,每次都是进行该操作,直到把所有点都连接。
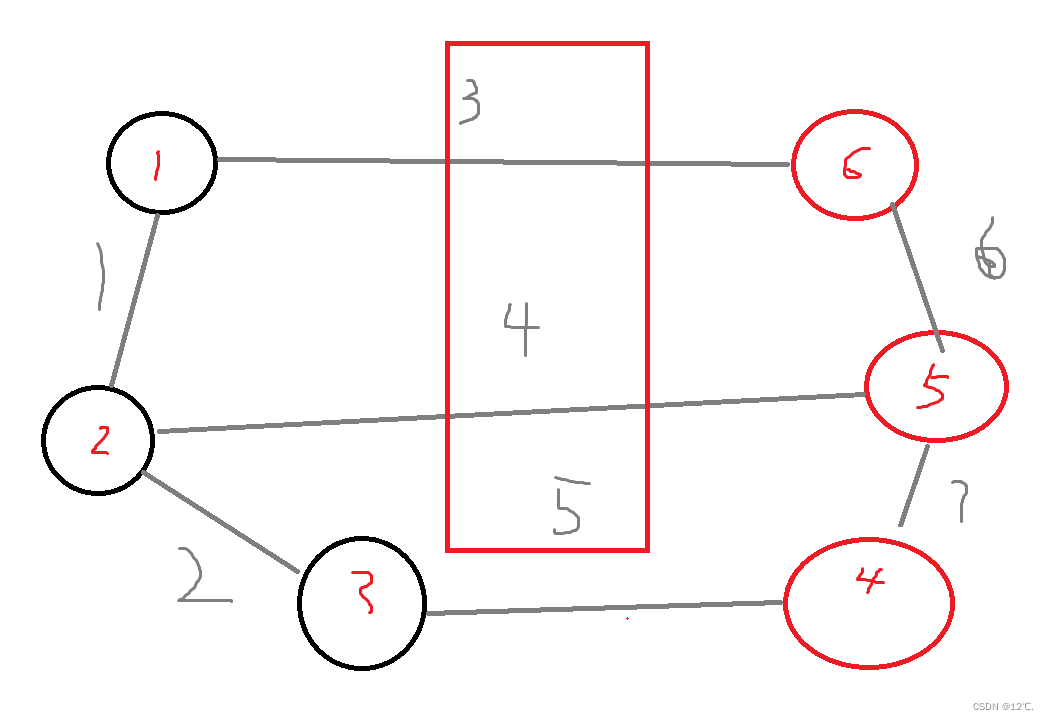
该算法与Dijkstra不同的地方是该算法每次存的是边权而不是路径权值和,该算法也不会受到负权值环的影响。
代码就是在Dijkstra的基础上改改就行,也是可以用堆来优化时间,但是不好的一点是空间复杂度比Kruskal要高。
时间复杂度为边的数量乘以顶点的数量n*m,常数也会比Kruskal大。
Kruskal算法
该算法就是优先最小代价的边,然后一条边一条的加到图里面,若是形成回路则直接删除该边。
例如;黑色边表示已经加到图里面的边,红色表示未添加的边,此时最小的边是2->6的边代价是3,但是这个边加进去之后会发现1、2、3形成回路,所以这条边直接删掉。然后最小的是1->3的边代价是4,这个边可以直接加进去,不会形成回路... ...
每次都是以这个模式进行。直到所有顶点都连通或着所有边都处理完。
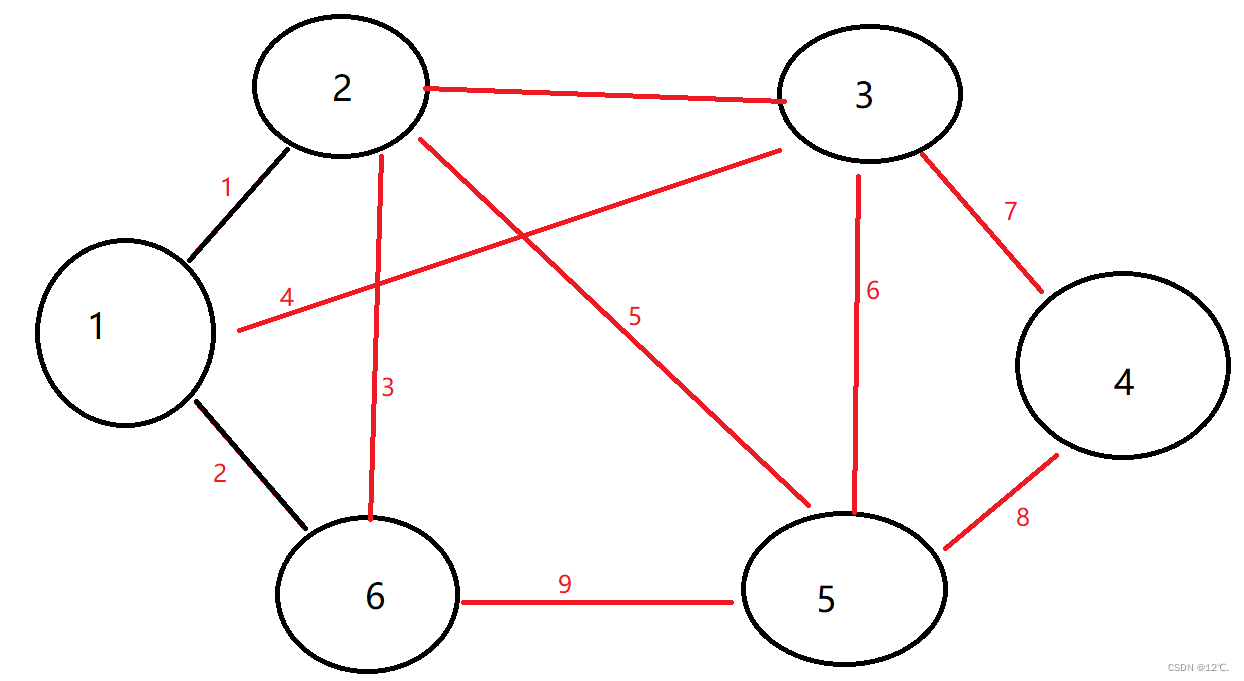
然后问题就是怎么判断顶点是否连通,这个地方就需要用到并查集来维护判断,假如该边的两个顶点的祖先相同,则说明两点已经连通,再将该边连通的话就会形成环。
该算法时间复杂度边的数量m*log(m);空间复杂度相比于堆优化的Prim小。
int n, r;// 顶点数 边数
int father[N];
struct aa
{
int a, b, w;// 端点1 端点2 权值
};
aa o[M];
int find(int x)
{
if(father[x] == x) return x;
return father[x] = find(father[x]);
}
int Kruskal()
{
stable_sort(o, o + r, cmp);
int k = n - 1, sum = 0;
for(int i = 0; i < r; i ++)// r为边的数量
{
int a = find(o[i].a), b = find(o[i].b);
if(a == b) continue; // 回路
k --;
sum += o[i].w;
father[b] = a; // 连通两点
if(k == 0) break; // 所有顶点都处理完
}
return sum; // 最小连通代价
}