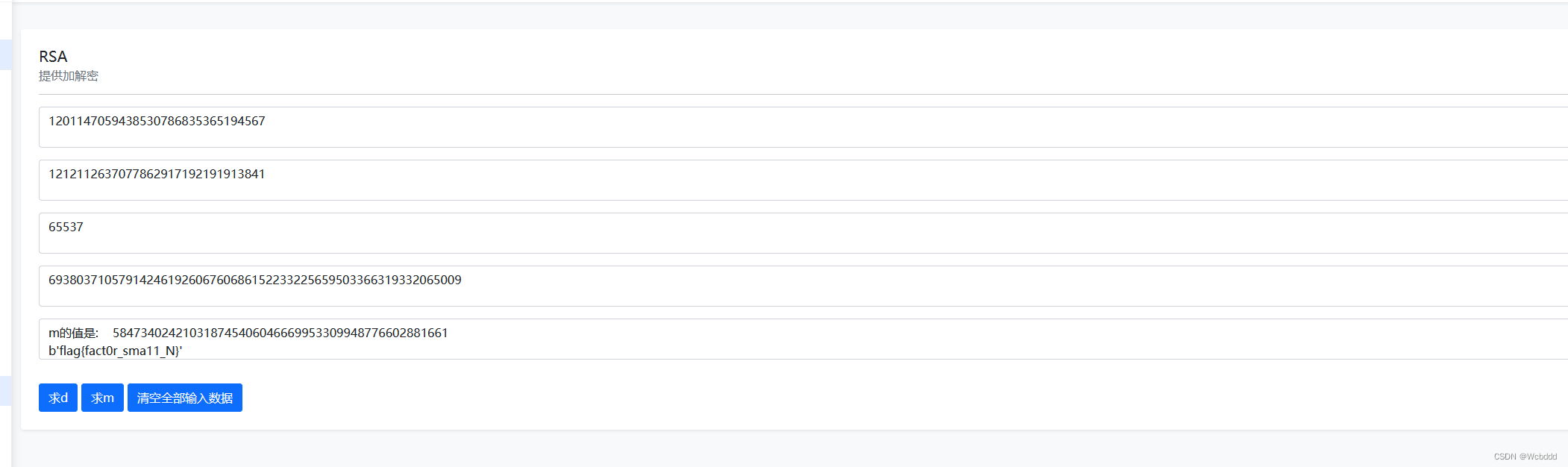
题目

n(n<=2e5)个点的树，

从起点s出发，每次等概率选择一条边，随机游走到相邻点

若走到t，则停止，问每个点经过的期望次数，答案对998244353取模

思路来源

DLUT_Zeratul讲解

题解

需要分成三部分考虑，

①s->t这条链，将这条链上的边定向，经过的次数，正向边=反向边+1

②对于s->t链上的点u(u可以等于s，u不可以等于t)，将u和s->t链之间的边断开后，u的子树内的点

对于子树内的点，正向边=反向边

③将t与s->t链之间的边断开后，t的子树内的点

由于走到t即停止，所以这部分子树点的期望次数等于0

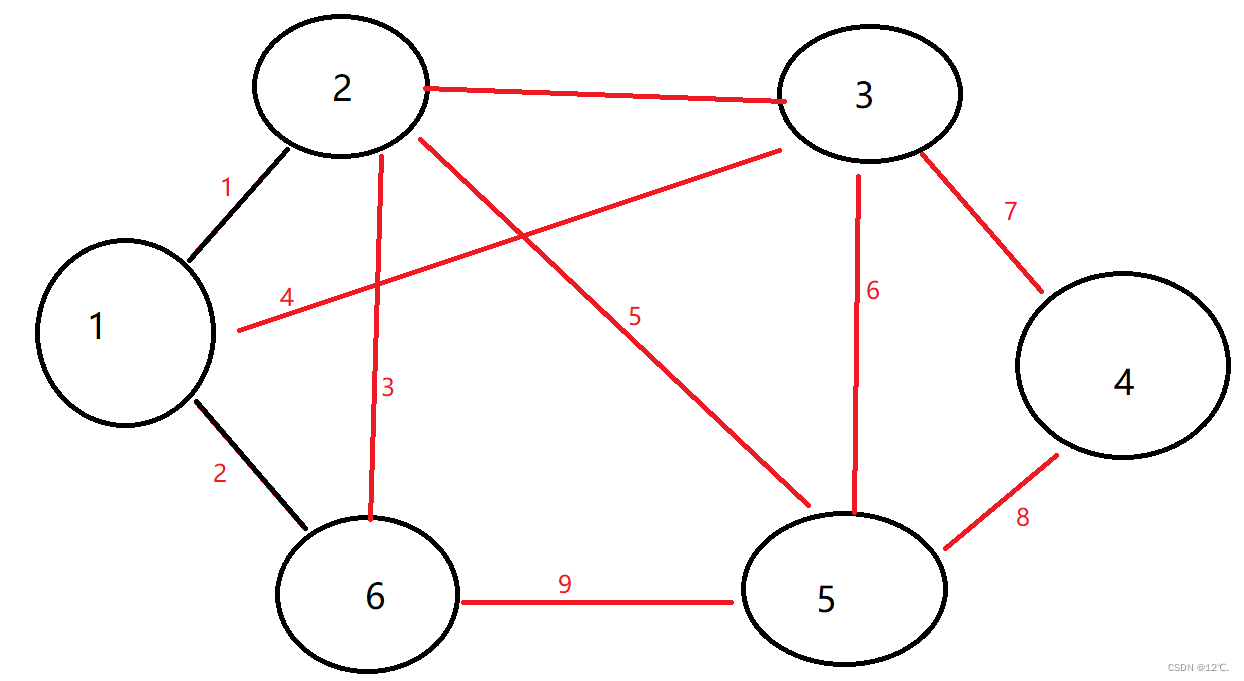
举个例子，以n=6，s=3，t=5这棵树为例

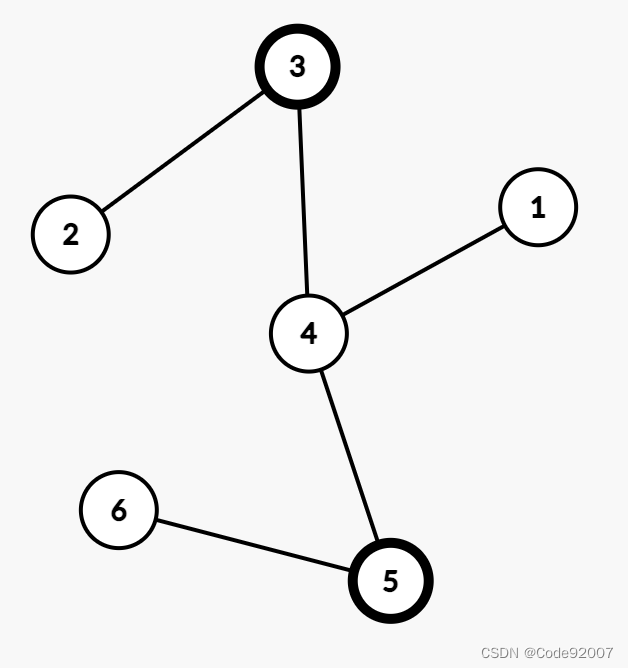
①部分，为点3、点4、点5，即3->4->5这条链

②部分，为点2、点1

③部分，为点6

记dp[i]为点i经过的期望次数，

记一条有向边(u,v)走的期望次数为，

根据期望定义，有

1. 当i!=t时，一条边i->x走的次数为，其中d[i]为点i的度

2. 当i=t时，一条边i->x走的次数为0，因为走到t后，就会立刻停止

然后就可以转移了

1. dp[t]=1，终点只会被经过一次

2. 先求①，根据，其中u->v为正向边，v->u为反向边

即，，求得dp[u]

3. 再求②，根据

即，，求得dp[u]

4. ③部分的值均为0，就无需再求了

代码

#include<iostream>
#include<vector>
using namespace std;
const int N=2e5+10,mod=998244353;
int n,s,t,u,v;
int dp[N]; // dp[i]:i点经过次数的期望
vector<int>e[N];
bool vis[N],has[N];
int modpow(int x,int n,int mod){
    int res=1;
    for(;n;n>>=1,x=1ll*x*x%mod){
        if(n&1)res=1ll*res*x%mod;
    }
    return res;
}
int inv(int x){
    return modpow(x,mod-2,mod);
}
int d(int x){
    return (int)(e[x].size());
}
void dfs(int u){
    vis[u]=1;
    for(auto &v:e[u]){
        if(vis[v])continue;
        dfs(v);
        if(!has[v])continue;
        dp[u]=1ll*((v==t?0:1ll*dp[v]*inv(d(v)))+1)%mod*d(u)%mod;// dp[u]/d[u]=(dp[v]/d[v])+1，其中从t再走出来的可能性是0
        has[u]=1;
    }
    if(u==t){
        dp[u]=1;
        has[u]=1;
    }
}
void dfs2(int u){
    vis[u]=1;
    for(auto &v:e[u]){
        if(vis[v])continue;
        if(has[u] && u!=t && !has[v]){
            dp[v]=1ll*(1ll*dp[u]*inv(d(u))%mod)*d(v)%mod;// dp[u]/d[u]=dp[v]/d[v]，其中从t再走出来的可能性是0
            has[v]=1;
        }
        dfs2(v);
    }
}
int main(){
    scanf("%d%d%d",&n,&s,&t);
    for(int i=1;i<n;++i){
        scanf("%d%d",&u,&v);
        e[u].push_back(v);
        e[v].push_back(u);
    }
    dfs(s);
    for(int i=1;i<=n;++i)vis[i]=0;
    dfs2(s);
    for(int i=1;i<=n;++i){
        printf("%d%c",dp[i]," \n"[i==n]);
    }
    return 0;
}