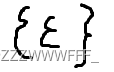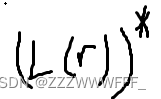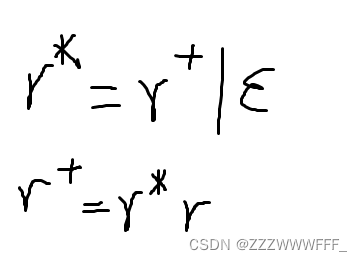编译原理期末复习简记（更新中~）

注意：该复习简记只是针对我校期末该课程复习纲要进行的，仅供参考

第一章引论

编译程序是什么？

编译程序是一个涉及分析和综合的复杂系统

编译程序组成

编译程序通常由以下内容组成

词法分析器
输入组成源程序的字符串
输出记号/单词序列
语法分析器
输入单词序列
输出语法单位（不同层次的语法成分）
语义分析与中间代码生成器
输入语法单位
输出中间代码
代码优化器
输入中间代码
输出中间代码
目标代码生成器
输入中间代码
输出目标程序
符号表管理器
与编译程序的全过程相关
功能：按照编译过程的信息需求，组织符号表，维护表格，提供信息服务
出错处理器
使得出错的地方尽量小，且编译程序能继续运行

第二章高级语言及文法

首先简单认识高级程序设计语言中的基本成分

单词
语句（单词组成的串，也叫句子）
程序（语句组成的串）
语言（语句的集合）

下面是学习这一章之前的必备概念认识

字母表

它是一个非空有穷集合（注意包含了集合的概念，即元素不能重复）
不可分性，类似\n，\t也是一个字符
字母表的乘积怎么计算？使用其中一个字母表的的每一个字符去拼接另一个字母表的每一个字符
字母表的N次幂，与字母表的乘积计算类似，需要注意的是0次幂的结果为由空字符组成的集合
字母表的正闭包（字母表的1次幂并2次幂并3次幂.......）
字母表的克林闭包（正闭包并上空集）

句子x

x是字母表克林闭包的一个元素，那么x为该字母表的一个句子
当且仅当两个句子的对应位置上的字符都相等，两个句子相等
句子也被称为字行串字符串字符行
句子的一个出现，例如字母表{a,b}，则abaabb为一个句子，那么a的第一个出现在句子首部，第二个出现在句子的第3个字符
句子的长度，使用绝对值符号，例如字符串bbaa的长度为4
注意空串符号长度为0 但是空串符号组成的一个集合长度为1
句子的并置/连结，例如两个串x=001，y=1101，那么xy=0011101
句子的前缀、真前缀、后缀、真后缀，真前缀与真后缀不包括句子本身，空串属于这里的四个概念
用字母与字母右上角一个T代表x的倒序，例如abc的倒序为cba
公共前缀最大公共前缀公共后缀最大公共后缀
子串（连续的），例如x=0101的子串有空串， 0，1，01，10，010，101，0101
公共子串，即两个句子的同时拥有同一个子串
最大公共子串（这里概念指的是长度），最大公共子串不唯一

语言

从字母表的克林闭包中选一些句子组成的集合叫做语言，其中语言的一个元素叫句子
有穷语言，无穷语言
语言的乘积参考字母表的乘积

文法的定义

文法的形式定义如下

文法G是一个四元组（V,T,P,S）

V代表变量/语法变量/非终结符，表示一个集合，变量也称为语法范畴
T代表终结符
V并T并空串中的符号统称为语法符号/文法符号
P为产生式/定义式/语法规则，类似a->b这样的结构，读作a定义为b，每一个产生式的左部为V与T的正闭包，右部为V与T的克林闭包
S为文法的开始符号
一般使用小写字母表示T，大写字母表示V，且第一个产生式的左部为该文法的开始符号

我们需要学会得到一个文法所描述的语言是什么

定义L(G)={w|S经过若干次推导得到w并且w是T的克林闭包}

那么如文法 C->a|b|c D->d|e E->C|D

L(C)={a,b,c} L(D)={d,e} L(E)={a,b,c,d,e}

直到我们推到开始符号S，那么L(S)即所给文法定义的语言，其中该集合的每一个元素都是该语言的一个句子

反过来我们需要判断某一个句子是否属于某文法

可以通过推导/规约的办法进行判断

什么是句型

如果我们可以通过开始符号S经过若干次推导得到一个类似产生式左部的"串"，那么这个"串"就叫句型，也就是说，句型可能含有非终结符，对比句子，句子绝对不含非终结符

因此句子一定是句型，句型不一定是句子

文法的分类

根据对产生式要求的不同，我们将文法分为4类（英文也要掌握）

0型文法/短语结构文法（phrase structure grammar,PSG），对应的L(G)称为0型语言/短语结构语言（PSL）/递归可枚举集
对产生式无约束，即任何文法都是0型文法
1型文法/上下文有关文法（context sensitive grammar,CSG），对应的有1型语言，上下文有关语言（CSL）
要求产生式右部长度>=左部
2型文法/上下文无关文法（context-free grammar,CFG），对应有2型语言，上下文无关语言（CFL）
约束是产生式右部长度>=左部且左部属于非终结符（且长度为1）
3型文法/正则文法（regular grammar,RG），对应3型语言，正则语言/正规语言（RL）
产生式要么类似A->w要么A->wB，其中A,B是非终结符，w是终结符的正闭包
正则文法与右线性文法的定义相同，并且可以证明左线性文法与右线性文法等价，因此二者统称正则文法
注意这四种文法都可以包含右部为空的产生式

语法树

语法树也称为分析树/推导树/派生树，每一个节点代表一个语法符号，如果分别将语法树的叶子按照从左到右的顺序排列，即得到一个结果，树根为文法的开始符号

注意这里的语法树只针对CFG

以某一颗树的节点A作为根得到的子树称为A-子树

短语

短语的概念是相对于句型来说的，句型的语法树的任意一个层数>=2的A-子树的结果(语法树的叶子按照从左到右的顺序排列)是它的短语，如果层数为2，那么是直接短语

推论：一个句型的短语数量<=对应语法树的中间节点数量（根节点也算中间节点）

总结：要想得到一个句型的短语，那么找到该句型的所有中间节点作为子树的根，找到所有子树的结果即可

句柄

G的句型的最左直接短语（树中最左边的直接短语）就是句柄

最左推导

a是G的一个句型，如果在a的推导过程中，每一步都是对当前句型的最左变量进行替换，那么称该推导为最左推导

且每一步得到的句型称为左句型

相应的规约称为最右规约

如果在a的推导过程中每一步对当前句型的最右变量进行替换，则称该推导为最右推导，每一步得到的句型也称为右句型，对应的最左规约

其中最右推导为规范推导，最左规约为规范规约，二者产生的句型称为规范句型

二义性

学会构建语法树并判断某个语法树是否存在二义性即可，做题时只需给出反例即可

素短语

在得到某个句型的所有短语后，按照从后往前进行判断即可

参考资料

第三章词法分析

什么是词法分析

简单来说，词法分析器读入表示源程序的字符流，按照程序功能等价的要求，将其转换成对应的单词序列，并且剔除其中的空格、注解等不影响程序语义的字符

单词的分类

关键字/基本字，类似程序设计语言中的while，if，int这些，此外如果某些关键字不允许被使用的话，我们称其为保留字
标识符，用于表示各种名字，例如变量名
常数
运算符
分界符，类似逗号，分号

正则表达式

根据前面所学我们可以使用正则文法去表示某一种单词，此外我们还可以使用正则表达式表示某种单词

正则表达式简称正则式/正规式，正则表达式与正则文法是等价的，不过正则表达式可以容易看出单词的结构

一个字母表上的正则表达式及其表示的语言定义如下

表示字母表上的一个正则表达式，表示空集
是字母表上的一个正则表达式，表示语言
对于字母表上的字母a，a是字母表上的一个正则表达式,它表示的正则语言是{a}
假设r和s都是字母表上的正则表达式，他们表示的语言分别为L(r)，L(s)，则：
(r)也是字母表上的正则表达式，它表示的语言为L(r)
(r|s)也是字母表上的正则表达式，它表示的语言为L(r)并L(s)
也是字母表上的正则表达式，它表示的语言为L(r)L(s)
也是字母表上的正则表达式，它表示的语言为

只有经过有限次上述规则得到的表达式才是字母表上的正则表达式

注意上面的乘号可以省略，|可以被+替代注意上面的乘号可以省略，|可以被+替代，并且闭包符号的优先级大于乘号，最后是或|

如果正则表达式r与s表示的语言相同，即L(r)=L(s)，则称两个正则表达式等价记作r=s

正则表达式所表示的语言称为正则集=正则语言

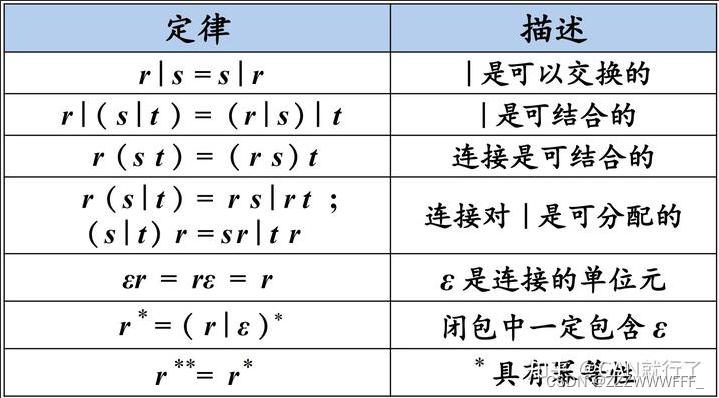
正则表达式的代数性质

补充克林闭包与正闭包

补充0或一个

？是一元操作符，表示“0或一个”

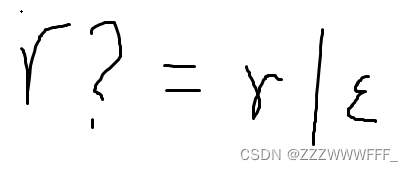
补充字符类

[ abc ]（其中a、b和c是字母表中的符号）表示正则表达式a|b|c

正则文法与正则表达式之间的转换

根据正则文法构建等价的正则表达式

根据上图所示的规则进行操作即可，注意不要漏情况了

将正则表达式转换成等价的正则文法

首先定义正则定义式/正规定义式的概念，简单的说就是形如A->r的式子，其中左部为一个语法变量，右部为一个正则表达式

接着根据上图规则进行分解即可

注意一点，转换出的是“正则文法即3类文法”，因此也要符合其规则

有穷状态自动机

首先认识什么是有穷状态自动机

其物理模型如下

因此我们对有穷自动状态机(FA)有如下定义

与前面类似的如果M1与M2都是FA，如果L(M1)=L(M2)，那么表示两个自动机是等价的

上面介绍的是确定的有穷状态自动机（DFA），如果状态转移函数存在空格子，那么则该自动机称为非确定的有穷状态自动机（NFA）

状态转换图

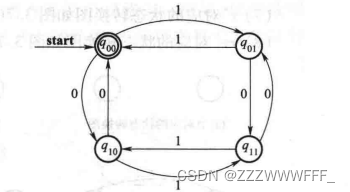
状态转换图也叫状态转移图，用于表示有穷状态自动机

如上图所示，每一个圆圈里的代表一个状态，其中有start指针指向的为开始状态，双圆圈表示终止状态/接受状态，弧表示在某个状态下读入某个内容时应该转移到什么状态

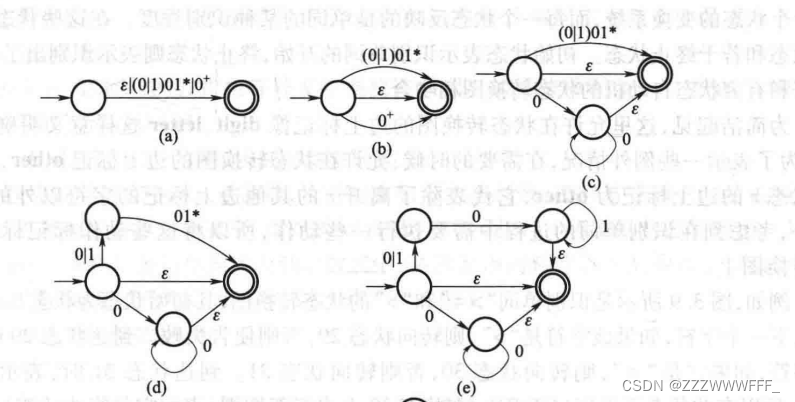
正则表达式转换为状态转换图

二者的“语法转换”如下图所示

例题