一、1312. 让字符串成为回文串的最少插入次数

1.题目简介

1312. 让字符串成为回文串的最少插入次数
给你一个字符串 s ，每一次操作你都可以在字符串的任意位置插入任意字符。
请你返回让 s 成为回文串的最少操作次数。
「回文串」是正读和反读都相同的字符串。
在这里插入图片描述

2.解题思路

3.代码

class Solution {
public:
    int minInsertions(string s) {
        int n = s.size();
        //1.判断出字符串中最长回文子序列
        vector<int> v(n, 0);
        vector<vector<int>> dp(n, v);
        //dp[i][j]表示以i为结尾以j为开始的最长回文子序列元素个数
        //初始化
        for(int i = 0;i < n; ++i)
        {
            dp[i][i] = 1;
        }
        for(int i = 0;i < n; ++i)
        {
            for(int j = i - 1;j >= 0; --j)
            {
                if(s[i] == s[j])//如果相等，则回文子序列加2元素
                {
                    dp[i][j] = dp[i - 1][j + 1] + 2;
                }
                else//如果不相等，则它的回文子序列为i或j往前遍历一个位置对应的回文子序列的较大值
                {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j + 1]);
                }
            }
        }
        int a = dp[n - 1][0];
        //2.用总元素个数减去最长回文子序列的元素个数
        return n - a;
    }
};

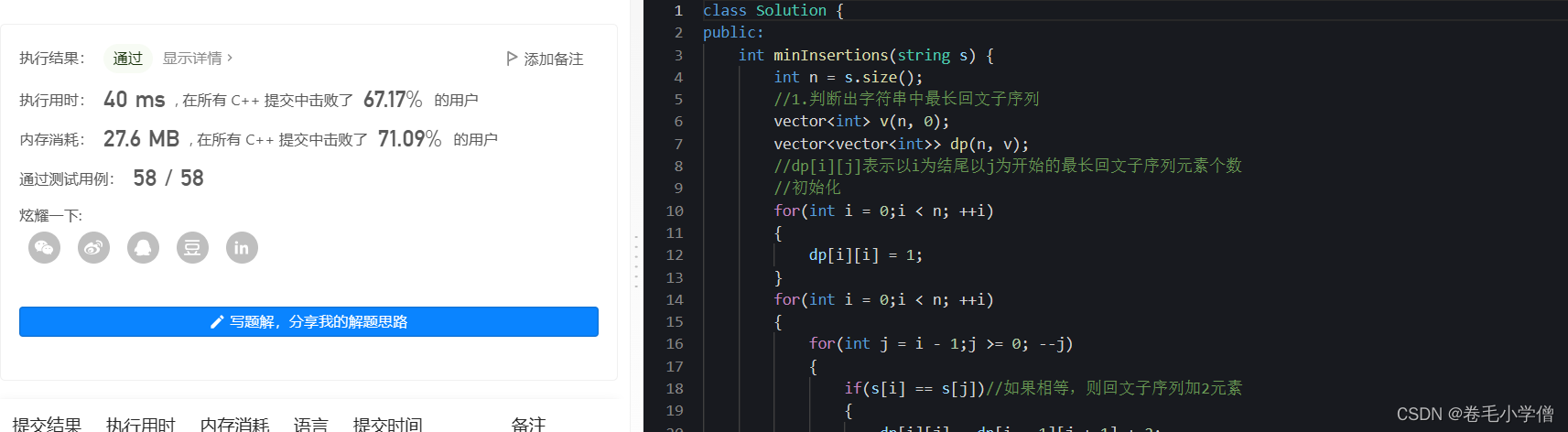
4.运行结果

在这里插入图片描述

二、1143. 最长公共子序列

1.题目简介

1143. 最长公共子序列
给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。
一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的公共子序列是这两个字符串所共同拥有的子序列。
在这里插入图片描述

2.解题思路

3.代码

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<int> v(text2.size() + 1, 0);
        vector<vector<int>> dp(text1.size() + 1, v);
        //dp[i][j]表示以i - 1为结尾的text1字符串和以j - 1为结尾的text2这两个字符串的最长公共子序列(为啥要-1呢？为了方便计算i - 1和j - 1的值，而不用很麻烦的初始化i=0和j=0的情况，实际上就是将i和j作为了长度而不是坐标)
        for(int i = 1;i <= text1.size(); ++i)
        {
            for(int j = 1;j <= text2.size(); ++j)
            {
                if(text1[i - 1] == text2[j - 1])//如果i和j对应元素相等，就等于它们前一个元素对应的最长长度加一
                {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                else//如果不相等就等于它们分别前一个元素对应的最长长度的较大值
                {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

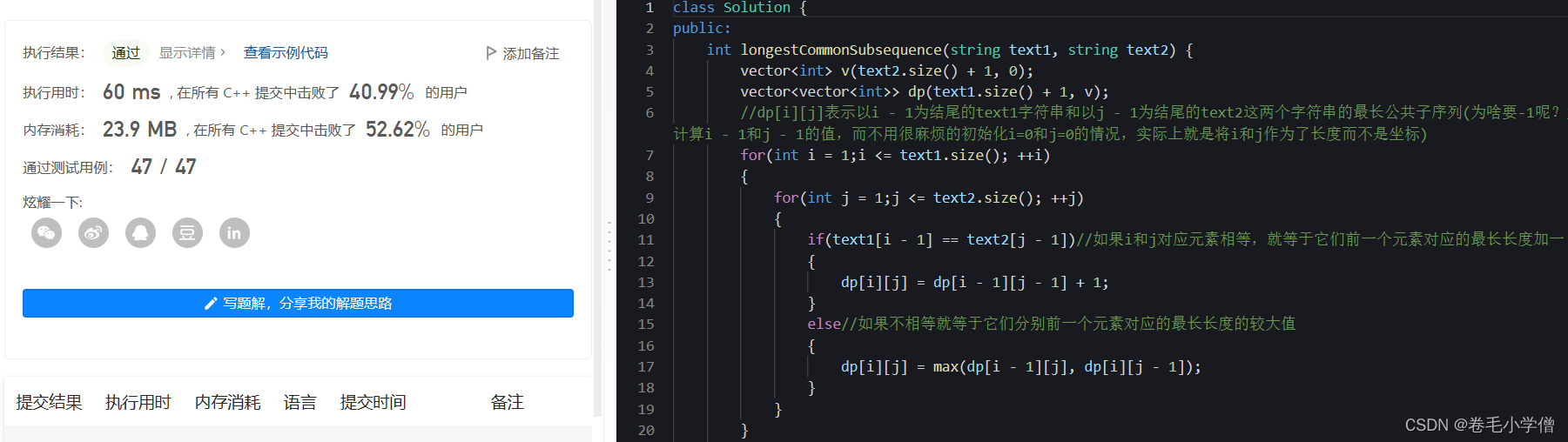
4.运行结果

在这里插入图片描述

三、1035. 不相交的线

1.题目简介

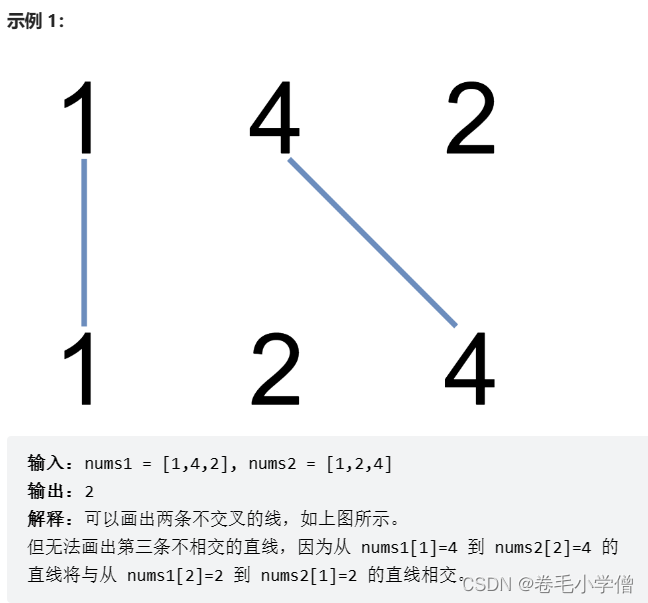
1035. 不相交的线
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足： nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。
请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。
以这种方法绘制线条，并返回可以绘制的最大连线数。
在这里插入图片描述

2.解题思路

3.代码

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        vector<int> v(nums2.size() + 1, 0);
        vector<vector<int>> dp(nums1.size() + 1, v);
        //实际上就是在求：以i为结尾的nums1数组和以j结尾的nums2数组两者之间的最长公共子序列
        for(int i = 1;i <= nums1.size(); ++i)
        {
            for(int j = 1;j <= nums2.size(); ++j)
            {
                if(nums1[i - 1] == nums2[j - 1])
                {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                else
                {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[nums1.size()][nums2.size()];
    }
};