参考资料：

• 《统计学习方法》李航
• 通俗理解信息熵 - 知乎 (zhihu.com)
• 拉格朗日函数为什么要先最大化？ - 知乎 (zhihu.com)

1 逻辑斯蒂回归

1.1 逻辑斯蒂回归

输入 $x=(x^{(1)},x^{(2)},\cdots ,x^{(n)},1{)}^T$ ，参数 $w=(w^{(1)},w^{(2)},\cdots ,w^{(n)},b{)}^T$ ，输出 Y ∈ { 0 , 1 } Y\in\lbrace0,1\rbrace Y∈{0,1} ，逻辑斯蒂模型为：
$$\begin{gathered} P(Y=1|x)=\frac{\exp (w\cdot x)}{1+\exp (w\cdot x)} \\ P(Y=0|x)=\frac{1}{1+\exp (w\cdot x)} \end{gathered}$$
逻辑斯蒂模型会比较两个条件概率的大小，将 $x$ 分到概率值较大的那一类。

1.2 参数估计

记 $\pi (x)=P(Y=1|x)$ ，则似然函数：
$$\begin{array}{rl}L(w)& =\prod _{i=1}^{N}P(y_i|x_i,w)\\ & =\prod _{i=1}^N{\pi }^{y_i}(x_i)(1-\pi (x){)}^{1-y_i}\end{array}$$
取对数，得：
$$\begin{array}{rl}l(w)& =\sum _{i=1}^N(y_i\log \pi (x_i)+(1-y_i)\log (1-\pi (x_i))\\ & =\sum _{i=1}^N(y_i\log \pi (x_i)+(1-y_i)\log (1-\pi (x_i)\left)\right)\\ & =\sum _{i=1}^N(y_i(w\cdot x_i)-\log (1+\exp (w\cdot x_i)))\end{array}$$

采用随机梯度下降法，求出梯度：
KaTeX parse error: Expected 'EOF', got '&' at position 36: …}{\partial w_j}&̲=\sum\limits_{i…

1.3 逻辑蒂斯的推广

逻辑蒂斯也适用于多分类模型：

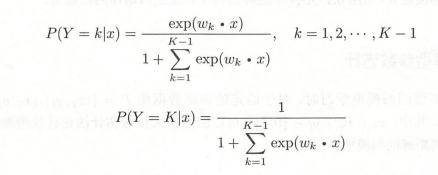
2 最大熵模型

2.1 最大熵原理

设随机变量 $X\sim P(X)$ ，则随机变量 $X$ 的熵 $H(X)$ 为：
$$H(X)=-\sum _{x}P(x)\log P(x)$$
进一步地，定义条件熵 $H(Y|X)$ 为：
$$H(Y|X)=\sum _{x}P(x)H(Y|X=x)=-\sum _{x,y}P(x)P(y|x)\log P(y|x)$$
所谓最大熵原理，就是在所有符合约束条件的模型中，选取熵最大的模型。

2.2 最大熵模型的定义

一般而言，我们的分类模型是一个条件概率分布 $P(Y|X)$ 。给定训练集 $T=\{(x_1,y_1),\cdots ,(x_N,y_N)\}$ ，我们可以得到联合经验分布和边缘经验分布：

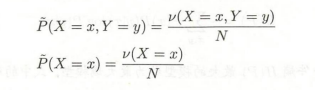
定义一组特征函数：
$$f_i(x,y)=\{\begin{array}{ll}1,& x和y满足某一事实\\ 0,& 其他\end{array}$$
特征函数关于经验分布 $\tilde{P}(X,Y)$ 的期望为：
$$E_{\tilde{P}}(f_i)=\sum _{x,y}\tilde{P}(x,y)f_i(x,y)$$
特征函数关于模型 $P(Y|X)$ 和经验分布 $\tilde{P}(X)$ 的期望为：
$$E_P(f_i)=\sum _{x,y}\tilde{P}(x)P(y|x)f_i(x,y)$$
模型的约束条件定义为：对所有的特征函数，有 $E_{\tilde{P}}(f_i)=E_P(f_i)$

2.3 最大熵模型的学习

最大熵的学习等价于约束最优化问题：

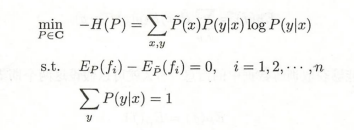
$C$ 为所有满足约束条件的模型的集合

引入拉格朗日乘数法：
$$L(P,w)=\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)+w_0(\sum _{y}p(y|x)-1)+\sum _{i=1}^n{w}_i(E_{\tilde{P}}(f_i)-E_P(f_i))$$
在一般的机器学习模型中，我们往往要先给出模型的表达式（ $P(Y|X;w)$ ），然后通过训练集来选取合适的参数。所以，我们要试着改写优化问题，使之能向一般的机器学习模型靠拢。

首先，上述最优化问题等价于：
$$\underset{P\in C}{\min }\underset{w}{\max }L(P,w)$$
这是因为如果所有约束条件均被满足，则必有 $-H(P)=\underset{w}{\max }L(P,w)$ ；如果存在某个约束条件不被满足，则一定可以通过调整对应参数，使得 $\underset{w}{\max }L(P,w)=+\infty$ ，这保证了通过 $\min \max$ 方式得到的解，一定是符合约束条件的解。

然后，我们根据拉格朗日对偶性得到对偶问题：
$$\underset{w}{\max }\underset{P\in C}{\min }L(P,w)$$
首先求解 $\underset{P\in C}{\min }L(P,w)$ :
$$\begin{array}{rl}\frac{\partial L(P,w)}{\partial P}& =\sum _{x,y}\tilde{P}(x)(1+\log P(y|x))+\sum _y{w}_0-\sum _{i=1}^n(w_i\sum _{x,y}\tilde{P}(x)f_i(x,y))\\ & =\sum _{x,y}\tilde{P}(x)(1+\log P(y|x)-w_0-\sum _{i=1}^n{w}_i{f}_i(x,y))\end{array}$$
令偏导数为 $0$ ，在 $\tilde{P}(x)>0$ 的情况下，有：
$$P(y|x)=\frac{\exp (\sum _{i=1}^n{w}_i{f}_i(x,y))}{\exp (1-w_0)}$$
通过 $\sum _{y}P(y|x)=1$ 消去 $w_0$ 得：
$$P(y|x)=\frac{1}{Z_w(x)}\exp (\sum _{i=1}^n{w}_i{f}_i(x,y))$$
其中：
$$Z_w(x)=\sum _y\exp (\sum _{i=1}^n{w}_i{f}_i(x,y))$$
此时，将 $P(y|x)$ 代回 $L(P,w)$ ，再求出 $\underset{w}{\max }L(P,w)$ 即可。

3 模型学习的最优化算法

3.1 改进的迭代尺度法（IIS）

IIS是最大熵模型的最优化算法，其想法是根据当前的参数向量 $w=(w_1,w_2,\cdots ,w_n{)}^T$ 找到一个 $\delta$ ，使得似然函数 $L(w+\delta )\ge L(w)$ 。实际操作时，通常是构造一个似然函数改变量的下界 $B(\delta |w)$，然后取 $\delta$ 为下界函数的最大值点。

已知最大熵模型为：
$$P(y|x)=\frac{1}{Z_w(x)}\exp (\sum _{i=1}^n{w}_i{f}_i(x,y))$$
其中：
$$Z_w(x)=\sum _y\exp (\sum _{i=1}^n{w}_i{f}_i(x,y))$$
对数似然函数为：
$$\begin{array}{rl}L(w)& =\sum _{i=1}^N\log P(y_i|x_i,w)\\ & =\sum _{x,y}\tilde{P}(x,y)\log P(y|x,w)\end{array}$$

其实第一行的式子并不等于第二行的式子，但二者的变化趋势是相同的。