目录

方向导数

方向导数和偏导数的区别就是：方向不同。仅此而已。

我们常说的偏导数无非就是对x轴求偏导，对y求偏导。而方向导数则是对x轴与y轴之间的某一新方向求导数。

还是用一下上次的图，这里我在x轴和y轴之间的平面上自己画了一个方向，并且与x轴夹角为α。

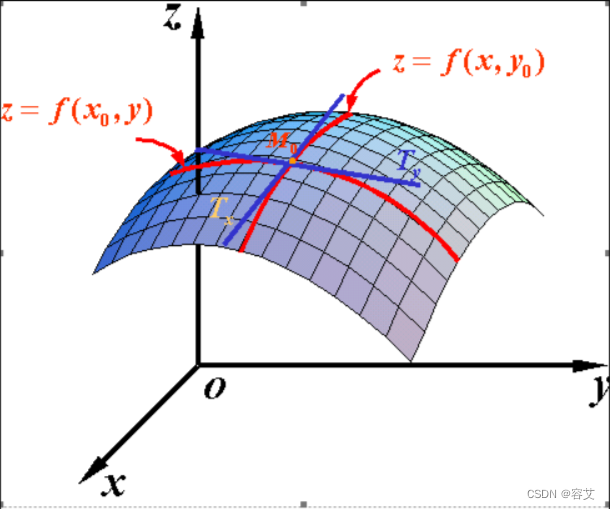
那么我们的z既然可以对x方向或y方向求偏导，自然也能对我新画的这个方向求“偏导”，这个“偏导”就是方向导数。

设这个新方向为l，因为这个方向导数和x与y轴有夹角关系，所以大可以用函数对x的偏导和y的偏导来表达，即：

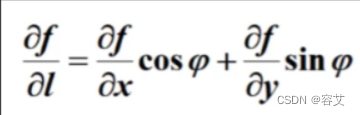
梯度

直接上梯度定义公式：

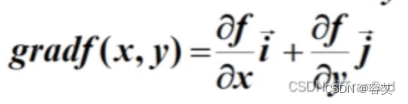
我自己理解成是：对于x求偏导的结果与对y求偏导的结果的“向量和”。这并不一定是45度的，因为虽然两个偏导向量的夹角是90度，但大小不同。假如函数z此时在x方向上上升很快，则梯度会被拉偏至x轴。

某点的梯度，也就是函数在某点上升最快的方向。给了一个函数，其在各个点变化最快的方向就固定了，就是梯度方向。

方向导数和梯度的关系

方向导数最大的方向，也就是梯度方向。