目录

一、说明

二、相关理论

2.1 何为相关

2.2 相关的前提

2.3  Correlation Matrix是个啥？

2.4 皮尔逊相关系数

三、Python演示如何创建相关矩阵

四、数据可视化观察

五、后记

---

一、说明

        本教程介绍如何在 Python 中创建和解释相关矩阵。然而，创建之前还是需要一些条件的，首先要检验数据的相关性。如果明显不相关，相关矩阵没有意义。其次，相关性的解释，相关的展现也是一个重要话题。

二、相关理论

2.1 何为相关

        1 无论是自相关还是互相关，都是描述的几个列向量之间的事情，列向量组合起来就变成了矩阵。

        2 自相关函数指的是列向量 的 相关系数 构成的函数，对于离散序列，自相关函数的变量就是序列的时间差，也就是E [x (k)x (k-t)]，当t=0时，求的就是均方值。

        3 相关矩阵出来的就是矩阵 的各个列之间的互相关系数，对角线是样本序列的方差，其他是各个样本序列的 协方差 ，也就是对应时刻的数据乘积的均值。

2.2 相关的前提

        相关分析前，首先通过观察散点图了解变量间大致的关系情况。

        如果变量之间不存在相互关系，那么在散点图上就会表现为随机分布的离散的点，如果存在某种相关性，那么大部分的数据点就会相对密集并以某种趋势呈现。

2.3  Correlation Matrix是个啥？

        Correlation Matrix是指将多个变量之间的相关系数放在一个表格中展示，并以矩阵（Matrix）形式呈现的一种统计工具。在Correlation Matrix中，每个变量都与其他所有变量之间的相关系数都呈现出来，这有助于我们了解变量之间的相关关系。Correlation Matrix通常用于探索性数据分析中，可以通过可视化或数值方式展示变量之间的相关性，从而帮助我们了解变量之间的关系，进而做出合理的决策。

2.4 皮尔逊相关系数

        量化两个变量之间关系的一种方法是使用皮尔逊相关系数，它是两个变量之间线性关联的度量。它衡量了两个变量之间的线性关系强度和方向，它的值介于 -1 和 1 之间，其中：

• -1 表示完全负线性相关。
• 0 表示没有线性相关。
• 1 表示完全正线性相关。

        相关系数离零越远，两个变量之间的相关性越强。

        但在某些情况下，我们想要了解不仅仅是一对变量之间的相关性。在这些情况下，我们可以创建一个相关矩阵，它是一个方表，显示多个变量成对组合之间的相关系数。

三、Python演示如何创建相关矩阵

        使用以下步骤在 Python 中创建相关矩阵。下列以某个篮球对为例生成一组比赛数据：助攻、篮板、得分的关系，以8场篮球的比赛统计说事。

Step 1: 先生成数据集.

import pandas as pd

data = {'助攻次数': [4, 5, 5, 6, 7, 8, 8, 10],
        '篮板球': [12, 14, 13, 7, 8, 8, 9, 13],
        '得分': [22, 24, 26, 26, 29, 32, 20, 14]
        }

df = pd.DataFrame(data, columns=['assists','rebounds','points'])

        以上用字典生成一个pd.DataFrame,表格如下： 

df

   assist  rebounds  points
0	4	12	22
1	5	14	24
2	5	13	26
3	6	7	26
4	7	8	29
5	8	8	32
6	8	9	20
7	10	13	14

Step 2: 生成相关矩阵.

#create correlation matrix
df.corr()

                assists   rebounds     points
assists        1.000000  -0.244861  -0.329573
rebounds      -0.244861   1.000000  -0.522092
points        -0.329573  -0.522092   1.000000

#create same correlation matrix with coefficients rounded to 3 decimals 
df.corr().round(3)
	       assists	rebounds  points
assists	         1.000	  -0.245  -0.330
rebounds	-0.245	   1.000  -0.522
points	        -0.330	  -0.522   1.000

Step 3:  解释相关矩阵

        沿表对角线的相关系数均等于 1，因为每个变量与其自身完全相关。所有其他相关系数表示变量的不同成对组合之间的相关性。例如：

• 助攻和篮板之间的相关系数为-0.245。
• 助攻数和得分之间的相关系数为-0.330。
• 篮板数和得分之间的相关系数为-0.522。

四、数据可视化观察

        数据科学最重要的技能之一就是数据可视化，在数据建模过程中，我们比较关心数据之间的相关性，而观察数据相关性我们使用最多的技能之一就是相关性矩阵。数据相关性矩阵可以让我们对数据之间的关联关系有更为直观的理解。这里简单汇总一下使用Python绘制传统相关性矩阵/下三角相关性矩阵/重点相关性矩阵的代码。

        3种常见方式：

• 1. 简单直接 - df.corr() 方法；
• 2. 常见好用 - heatmap 热力图；
• 3. 形象且有规律 - 正负相关关系分离的条形图。

Step 4: 可视化相关矩阵（可选）。

        您可以使用 pandas 中可用的样式选项来可视化相关矩阵：

corr = df.corr()
corr.style.background_gradient(cmap='coolwarm')

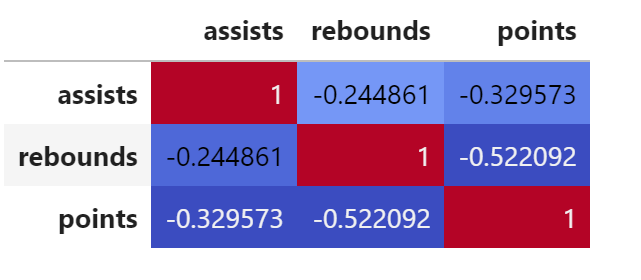
        您还可以更改 cmap 的参数以生成具有不同颜色的相关矩阵。

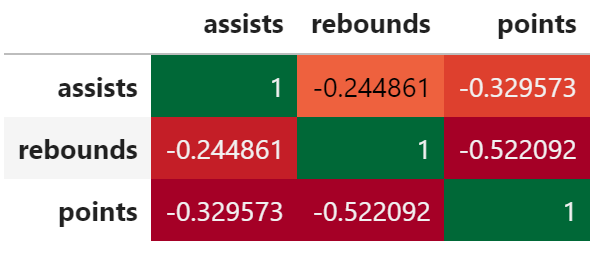
corr = df.corr()
corr.style.background_gradient(cmap='RdYlGn')

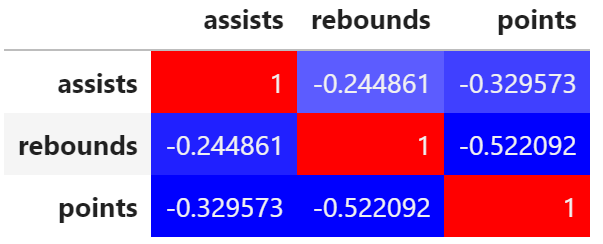
corr = df.corr()
corr.style.background_gradient(cmap='bwr')

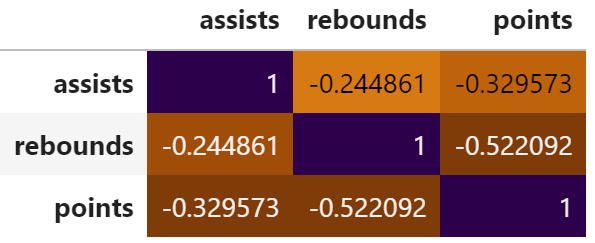
corr = df.corr()
corr.style.background_gradient(cmap='PuOr')

五、后记

        相关一般是和其它统计手段同时应用的。我们本文只讲相关矩阵生成部分，但不分析数据，因此，如何用python生成才是重点。