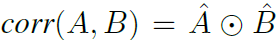引言

本文基于PyTorch实现条件随机场，实现CRF层参考论文Neural Architectures for Named Entity Recognition中关于CRF层的描述。包含大量的图解和例子说明，看完一定能理解！

论文地址： https://arxiv.org/pdf/1603.01360.pdf

也可参考论文笔记： [论文笔记]Neural Architectures for Named Entity Recognition

虽然在尽量控制篇幅，但还是得分成上下两篇：

---

下一篇： 动手实现条件随机场(下)

---

条件随机场

首先，简单介绍下(线性链)条件随机场，更详细的介绍可参考统计学习方法——条件随机场。

条件随机场(CRF)是一个概率无向图模型，为$p(y|x)$建模，因此它是一个判别模型。

其中$x$和$y$分别是观测序列和它对应的状态序列。CRF最常用的应用场景是序列标注任务，在该任务汇总，输入$x$就是要标注的序列，比如在NER任务中，就是单个字，但通常也可以认为是经过处理后的嵌入向量。而$y$是输入序列$x$中各个元素对应的标签序列。

以统计学习方法中的图为例，线性链条件随机场如上图所示，可以看到连线上没有箭头，所以是无向图模型。

每个$y_i$只与相邻结点$y_{i-1}$和$y_{i+1}$以及整个输入$x$有关。

对于这种无向图模型，我们需要手动定义特征函数，特征函数的取值为0或1。每个特征函数都有对应的权重，CRF模型学习的就是这个权重。特征函数比如中文分词中的SBME，B(词的开头)的后面只能是M(词的中间)或E(词的结尾)。

这里有两种特征函数，分别是状态特征函数和转移特征函数。状态特征函数描述的是当前观测输入和对应状态之间的连接，而转移特征函数描述的是前一个状态签和当前状态之间的连接：
$$P(y|x)=\frac{1}{Z(x)}\exp \left(\sum _{i,k}{\lambda }_k{t}_k(y_{i-1},y_i,x,i)+\sum _{i,l}{\mu }_l{s}_l(y_i,x,i)\right)\text{\hspace{1em}(1)}$$
式中，$t_k$和$s_l$分别是转移特征函数和状态特征函数，而${\lambda }_k$和${\mu }_l$是对应的权值，${\sum }_{i,k}$表示两个求和写在一起。

$Z(x)$是规范化因子，使得满足概率定义，求和是在所有可能的输出序列上进行的。
$$Z(x)=\sum _y\exp \left(\sum _{i,k}{\lambda }_k{t}_k(y_{i-1},y_i,x,i)+\sum _{i,l}{\mu }_l{s}_l(y_i,x,i)\right)\text{\hspace{1em}(2)}$$
从这个形式上可以看出，CRF并未对观测序列$x$做任何假设。

其中$s_l$也称为发射分数(emission score)，表示由输入$x_i$得到状态$y_i$的可能性；$t_k$也称为转移分数，表示$y_{i-1}$后面是$y_i$的可能性。

现在比较麻烦的是$Z(x)$的计算，幸运的是在CRF中，我们可以利用动态规划逐步地计算它：

下面基于Pytorch实现CRF，同时为了好理解，以NER任务为例。NER常用的标签格式是BIO(Beginning-inside-outside) ： B代表一个实体的开始；I表示一个实体的剩余部分；O表示非实体。比如B-LOC表示地点实体的开始；人名实体的剩余部分用I-PER表示。

下面给出一些符合格式的例子：

• B-LOC/I-LOC/O/O ✔️
• B-PER/I-PER/O/O ✔️

再给出一些不符合格式的例子：

• B-LOC/I-PER/O ❌ I-PER只能出现在B-PER之后
• start/I-LOC/B-LOC/O ❌ 不可能从start标签到I-LOC

实现CRF

根据论文Neural Architectures for Named Entity Recognition中关于CRF层的描述。

对于一个输入序列：
$$X=(x_1,x_2,\cdots ,x_n)$$
记Bi-LSTM模型的输出为$P$，它是一个大小为$n\times k$的矩阵，$k$是不同标签的数量。表示输入序列中每个单词产生每个标签的得分(不是概率！)。比如$P_{i,j}$表示输入序列中第$i$个单词得到第$j$个标签的得分。这个矩阵$P$也称为发射得分(emission scores)矩阵。

对于某个预测标签序列
$$y=(y_1,y_2,\cdots ,y_n)$$
定义其对应的得分为
$$s(X,y)=\sum _{i=0}^n{A}_{y_i,y_{i+1}}+\sum _{i=1}^n{P}_{i,y_i}\text{\hspace{1em}(3)}$$
相当于公式$(1)$中括号内转移特征函数和状态特征函数的取值之和。

这里$A$是转移得分(trasition scores)矩阵，$A_{i,j}$表示从标签$i$到标签$j$的转移得分。另外也引入$y_0$和$y_n$分别表示句子的$\text{start}$和$\text{end}$标签，把这两个标签也加入到标签集，所以$A$是一个$k+2$大小的方阵。转移得分矩阵学的就是一些转移约束，比如上面介绍的那些

个人理解$P$建模了CRF中的带权重的状态特征函数，$A$建模了带权重的转移特征函数。

同时根据CRF势函数的定义，对得分取指数，然后除以所有可能的标签序列$\tilde{y}$的得分之和就得到了产生该序列$y$的概率：
$$p(y|X)=\frac{e^{s(x,y)}}{{\sum }_{\tilde{y}\in Y_X}{e}^{s(X,\tilde{y})}}\text{\hspace{1em}(4)}$$
这里$Y_X$代表对于输入句子$X$所有可能的标签序列(包括那些无意义的，即不符合语法或约束的)。

分母相当于CRF中的规范化因子$Z(x)$，也称为配分函数，相当于公式$(2)$。

如果$y$是正确标签序列，那么我们的目标是使得公式$(4)$的概率越大越好。

尽可能最大化正确标签序列的概率，对上式取对数，就得到了对数似然：
$$\log (p(y|X))=s(X,y)-\log \left(\sum _{\tilde{y}\in Y_x}{e}^{s(x,y)}\right)\text{\hspace{1em}(5)}$$
从上式可以看到，目的是鼓励模型产生正确的标签序列。通常我们习惯最小化损失，所以可以对上式取负数，变成负对数似然损失：
$$\mathcal{L}=-\log (p(y|X))=\log \left(\sum _{\tilde{y}\in Y_x}{e}^{s(x,y)}\right)-s(X,y)\text{\hspace{1em}(6)}$$
观察上式，发现由一个指数相加后取对数和一个得分组成，前者可能会出现数值溢出问题，可以通过log-sum-exp技巧解决，为了控制文章内容的长度，这里就不展开了，可以参考文章：一文弄懂LogSumExp技巧；后者就是给定(正确)标签序列$y$的得分，根据公式$(3)$就可以计算。

在解码时，通过维特比算法得到最有可能的标签序列：
$$y^{\ast }=\arg \underset{\tilde{y}\in Y_X}{\max }s(X,\tilde{y})\text{\hspace{1em}(7)}$$

根据上面的分析，得到我们要实现的CRF模型的整体代码框架如下：

import torch
import torch.nn as nn


class CRF(nn.Module):
    """
    条件随机场的实现。
    使用前向-后向算法计算输入的对数似然。参考论文 Neural Architectures for Named Entity Recognition 。
    基于Python3.10.9和torch-1.13.1
    """

    def __init__(
        self,
        num_tags: int,
        batch_first: bool = False,
    ) -> None:
        """初始化CRF的参数

        Args:
            num_tags (int): 标签数量
            batch_first (bool, optional): 是否batch维度在前，默认为False
        """

        pass

        

    def forward(
        self,
        emissions: torch.Tensor,
        tags: torch.LongTensor,
        mask: torch.ByteTensor | None = None,
        reduction: str = 'sum'
    ) -> torch.Tensor:
        """计算给定的标签序列tags的负对数似然

        Args:
            emissions (torch.Tensor):  发射分数P 形状 (seq_len, batch_size, num_tags), 代表序列中每个单词产生每个标签的得分
            tags (torch.LongTensor): 标签序列 如果batch_first=False 形状 (seq_len, batch_size) ，否则 形状为 (batch_size, seq_len)
            mask (torch.ByteTensor | None, optional): 表明哪些元素为填充符，和tags的形状一致。  如果batch_first=False  形状 (seq_len, batch_size) ，否则 形状为 (batch_size, seq_len)
                默认为None，表示没有填充符。
            reduction (str): 汇聚函数： none|sum|mean|token_mean 。 none：不应用汇聚函数； 默认为sum。

        Returns:
            torch.Tensor: 输入tags的负对数似然
        """
        pass

     

    def _compute_score(
        self,
        emissions: torch.Tensor,
        tags: torch.LongTensor,
        mask: torch.ByteTensor,
    ) -> torch.Tensor:
        """计算标签序列tags的得分


        Args:
            emissions (torch.Tensor): 发射分数P 形状 (seq_len, batch_size, num_tags)
            tags (torch.LongTensor): 标签序列 形状 (seq_len, batch_size)
            mask (torch.ByteTensor): 表明哪些元素为填充符 形状 (seq_len, batch_size)

        Returns:
            torch.Tensor: 批次内标签tags的得分， 形状(batch_size,)
        """
        pass

      

    def _compute_partition(
        self, emissions: torch.Tensor, mask: torch.ByteTensor
    ) -> torch.Tensor:
        """利用CRF的前向算法计算partition的分数

        Args:
            emissions (torch.Tensor): 发射分数P 形状 (seq_len, batch_size, num_tags)
            mask (torch.ByteTensor): 表明哪些元素为填充符  (seq_len, batch_size)

        Returns:
            torch.Tensor: 批次内的partition分数 形状(batch_size,)
        """
        pass
    
    
    def decode(
        self, emissions: torch.Tensor, mask: torch.ByteTensor = None
    ) -> list[list[int]]:
        """使用维特比算法找到最有可能的序列

        Args:
            emissions (torch.Tensor):  发射分数P 形状 (seq_len, batch_size, num_tags), 代表序列中每个单词产生每个标签的得分
            mask (torch.ByteTensor | None, optional): 表明哪些元素为填充符。  如果batch_first=False  形状 (seq_len, batch_size) ，否则 形状为 (batch_size, seq_len)
                默认为None，表示没有填充符。

        Returns:
            list[list[int]]: 批次内的最佳标签序列
        """
        pass

    def _viterbi(
        self, emissions: torch.Tensor, mask: torch.ByteTensor = None
    ) -> list[list[int]]:
        """维特比算法的实现

        Args:
            emissions (torch.Tensor): 发射分数P 形状 (seq_len, batch_size, num_tags)
            mask (torch.ByteTensor): 表明哪些元素为填充符 形状 (seq_len, batch_size)

        Returns:
            list[list[int]]: 批次内的最佳标签序列
        """
        pass
    

其中_compute_score计算的是$s(X,y)$；_compute_partition计算的是$\log \left({\sum }_{\tilde{y}\in Y_x}{e}^{s(x,y)}\right)$；forward利用_compute_score和_compute_partition得到损失；_viterbi计算的是公式$\arg {\max }_{\tilde{y}\in Y_X}s(X,\tilde{y})$。

下面一步一步地实现并解析以上方法的实现。在继续之前，不得不提到的是CRF模型只学习了转移分数，发射分数可以由Bi-LSTM或BERT得到。

定义CRF模型

首先定义CRF模型的初始化方法

    def __init__(
        self,
        num_tags: int,
        batch_first: bool = False,
    ) -> None:
        """初始化CRF的参数

        Args:
            num_tags (int): 标签数量
            batch_first (bool, optional): 是否batch维度在前，默认为False
        """

        pass

        super().__init__()
        self.num_tags = num_tags
        self.batch_first = batch_first

        # 转移分数(A)，表示两个标签之间转移的得分
        # transitions[i,j] 表示由第i个标签转移到第j个标签的得分(可以理解为 可能性/置信度)
        self.transitions = nn.Parameter(torch.Tensor(num_tags, num_tags))
        # 新引入了两个状态(标签)：start和end
        # 从start状态开始转移到所有其他状态的分数
        self.start_transitions = nn.Parameter(torch.Tensor(num_tags))
        # 从所有其他状态转移到end状态的分数
        self.end_transitions = nn.Parameter(torch.Tensor(num_tags))

        self.reset_parameters()

这里主要定义了转移分数矩阵，大小是标签个数×标签个数，为什么没加2呢，因为后把从start标签转移的分数和转移到end标签的分数单独定义了。

最后reset_parameters用来随机初始化参数，这里使用的是均匀分布，也可以尝试He初始化。CRF模型要学的东西就是这三个参数，它们可以通过梯度下降法来更新。

def reset_parameters(self) -> None:
    nn.init.uniform_(self.transitions, -0.1, 0.1)
    nn.init.uniform_(self.start_transitions, -0.1, 0.1)
    nn.init.uniform_(self.end_transitions, -0.1, 0.1)

定义前向传播

定义前向传播，计算损失。

def forward(
    self,
    emissions: torch.Tensor,
    tags: torch.LongTensor,
    mask: torch.ByteTensor | None = None,
) -> torch.Tensor:
    """计算给定的标签序列tags的负对数似然

    Args:
        emissions (torch.Tensor):  发射分数P 形状 (seq_len, batch_size, num_tags), 代表序列中每个单词产生每个标签的得分
        tags (torch.LongTensor): 标签序列 如果batch_first=False 形状 (seq_len, batch_size) ，否则 形状为 (batch_size, seq_len)
        mask (torch.ByteTensor | None, optional): 表明哪些元素为填充符，和tags的形状一致。  如果batch_first=False  形状 (seq_len, batch_size) ，否则 形状为 (batch_size, seq_len)
            默认为None，表示没有填充符。

    Returns:
        torch.Tensor: 输入tags的负对数似然
    """

    if mask is None:
        # mask 取值为0或1，这里1表示有效标签，默认都为有效标签
        mask = torch.ones_like(tags)

    if self.batch_first:
        # 转换为seq维度在前的形式
        emissions = emissions.permute(0, 1) # (seq_len, batch_size, num_tags)
        tags = tags.permute(0, 1) #  (seq_len, batch_size)
        mask = mask.permute(0, 1) #  (seq_len, batch_size)

    # 计算标签序列tags的得分
    score = self._compute_score(emissions, tags, mask)
    # 计算配分函数 partition Z(x)
    partition = self._compute_partition(emissions, mask)

    return partition - score

注意，这里统一设置成batch_first=False的形式，为了后续实现和阅读的方便。

下面分别来实现其中定义了两个_开头的函数，用_开头表示不希望调用者直接调用该方法。

计算标签序列得分

先给出实现，然后逐行代码图解分析。

def _compute_score(
      self,
      emissions: torch.Tensor,
      tags: torch.LongTensor,
      mask: torch.ByteTensor,
  ) -> torch.Tensor:
      """计算标签序列tags的得分


      Args:
          emissions (torch.Tensor): 发射分数P 形状 (seq_len, batch_size, num_tags)
          tags (torch.LongTensor): 标签序列 形状 (seq_len, batch_size)
          mask (torch.ByteTensor): 表明哪些元素为填充符 形状 (seq_len, batch_size)

      Returns:
          torch.Tensor: 批次内标签tags的得分， 形状(batch_size,)
      """

      seq_len, batch_size = tags.shape
      # first_tags (batch_size,)
      first_tags = tags[0]

      # 由start标签转移到批次内所有标签序列第一个标签的得分
      score = self.start_transitions[first_tags]
      # 加上 批次内第一个(index=0)发射得分，即批次内第0个输入产生批次内对应第0个标签的得分

      score += emissions[0, torch.arange(batch_size), first_tags]

      mask = mask.type_as(emissions)  # 类型保持一致
      # 这里的index从1开始，也就是第二个时间步开始
      for i in range(1, seq_len):
          # 第i-1个标签转移到第i个标签的得分 + 第i个单词产生第i个标签的得分
          # 乘以mask[i]不需要计算填充单词的得分
          score += (
              self.transitions[tags[i - 1], tags[i]]
              + emissions[i, torch.arange(batch_size), tags[i]]
          ) * mask[i]

      # last_tags = tags[-1] × 这是错误的！，因为可能包含填充单词
      valid_last_idx = mask.long().sum(dim=0) - 1  # 有效的最后一个索引
      last_tags = tags[valid_last_idx, torch.arange(batch_size)]

      # 最后加上最后一个标签转移到end标签的转移得分
      score += self.end_transitions[last_tags]

正如前面所说的，以NER任务为例。假设有两个实体PER、LOC。

一个打好标签的数据如下：

我 O
叫 O
李 B-PER
明 I-PER
， O
来 O
自 O
中 B-LOC
国 I-LOC
。 O

为了简单，我们只取前五个字我叫李明，和你好，组成一个批次。

图 1

假设标签对应的索引如下：

{"O" : 0, "B-PER" : 1, "I-PER": 2, "B-LOC": 3, "I-LOC": 4}

这五个标签在图1上按从上到下排列(青色圆圈)，其中第一列的下面写出了对应的标签，上图还指出了标签O所在的时间步。

我们看_compute_score的参数，它是已知(正确)标签序列，计算该标签序列对应的得分，即该函数的返回值。我们想要的目的是基于该输入序列，使得该标签序列的得分远远大于所有其他标签序列。

这里我们有两个句子组成了一个批次:

sentence1 = "你好，"
sentence2 = "我叫李明，"
tags1 = ["O", "O", "O"]
tags2 = ["O", "O","B-PER", "I-PER", "O"]

组成批次后，对应的标签序列为：

tensor([[0, 0],
        [0, 0],
        [1, 0],
        [2, 0],
        [0, 0]])

tags的形状是(seq_len, batch_size)，这里seq_len=5,batch_size=2，所以是一个5 × 2的矩阵，5行表示序列长度，2列表示批次大小，每一列代表一个标签序列。

比如输入序列我叫李明，对应的正确标签序列为O\O\B-PER\I-PER\O,该标签序列的连线已经在图1画好了。该标签序列对应的tags = [0,0,1,2,0]。

在该批次内，由于你好，的长度只有3，为了和最大长度5对齐，被填充到5，因此它对应的mask为[1,1,1,0,0]。而我叫李明，没有被填充，对应的 mask为 [1,1,1,1,1]。

mask = torch.ByteTensor([[1,1],[1,1],[1,1],[1,0],[1,0]])

剩下的参数emissions为底层网络计算出来的，这里假设该底层网络为Bi-LSTM，我们这里实现的是CRF层。Bi-LSTM+CRF是组成一个模型一起训练的。

first_tags = tags[0] #  (batch_size,)

tags 的形状已经是 (seq_len, batch_size)，因此tags[0]就是取该批次内所有标签序列的第一个标签，得到的维度是 (batch_size,)。

对于我们这个例子中，first_tags=tensor([0, 0])，即取tags矩阵中的第一行。

# 由start标签转移到批次内所有标签序列第一个标签的得分
score = self.start_transitions[first_tags]

直接定义score为start标签转移到第一个标签的得分。实际上计算的是图1中如图2所示的转移得分：

图2

因为在start标签处实际并没有输入，所以也不需要计算发射得分。

假设我们的转移得分和发射得分如下图3所示：

图3

我们这里的first_tags批次内的取值都是0，即对应O标签。所以，score=[-1.6891,-1.6891]，即start_transitions保存的转移到O标签的得分。这段代码执行结果如下：

这是start标签的转移得分，下面为了计算真正标签的转移得分，我们需要通过self.transitions[tags[i - 1], tags[i]]获取。现在我们考虑i的初始取值，如果i=0，那么就会有问题。因为令i=1直到i=seq_len-1。可以依次得到从第0个标签(非start)转移到第seq_len-1个标签(非end)的转移得分。

当用阿拉伯数字描述第几个时，代表的就是索引；用中文数字描述时，第一个相当于第0个，所以上面第seq_len-1个相当于最后一个标签，即第五个标签。除非特别说明，否则都不把start和end计算在内。

继续考虑发射得分的情况下，当i=1时，计算的应该是第二个标签的发射得分，这里漏掉了第一个标签的发射得分。因此下面把它加上：

score += emissions[0, torch.arange(batch_size), first_tags]

这是计算发射得分的通用代码，下面来解释一下。

首先，emissions的形状是(seq_len, batch_size, num_tags)。描述的是批次内输入的第几个时间步产生哪个标签的得分。

emissions[0, torch.arange(batch_size), first_tags]是所有批次内的第0个时间步产生对应标签的得分，这段代码的实际效果等同于：

[emissions[0, 0, 0],emissions[0, 1, 0]]

首先第一个维度seq_len取值固定为0，代表输入的第0个时间步；arange(2) = [0,1],first_tags=[0,0]会对应时间步进行组合，如上图所示。

意思是批次内第0个样本的第0个时间步取第0个标签的得分 和 批次内第1个样本的第0个时间步取第0个标签的得分。

这样我们计算出了批次内所有样本的第0个时间步的发射得分。

下面就可以写一个循环同时计算发射得分和转移得分了，整个函数做的事就是上面公式$(3)$。

 mask = mask.type_as(emissions)  # 类型保持一致 形状 (seq_len, batch_size)
# 这里的index从1开始，也就是第二个时间步开始
for i in range(1, seq_len):
    # 第i-1个标签转移到第i个标签的得分 + 第i个单词产生第i个标签的得分
    # 乘以mask[i]不需要计算填充单词的得分
    score += (
        self.transitions[tags[i - 1], tags[i]]
        + emissions[i, torch.arange(batch_size), tags[i]]
    ) * mask[i]

这里额外考虑的是mask来保证不会计算填充时间步的得分。

图4

假设如图4所示，通过上面的循环，现在现在计算到了第三个时间步，累计计算到的用红框框出。

此时，下一步我叫李明应该到I-PER标签，而你好，<pad><pad>下一个是填充标签，实际上不会累加到它所对应的score上去。第3个时间步mask取值如下：

注意score的形状保持为(batch_size,)，和mask[3]的维度一致，它们相乘就是对应时间步的元素相乘。某个得分乘0后再加到score中相当于没加。

最后，这个循环，计算了累计到seq_len-1时间步的转移得分和发射得分。

图5

但是注意，此时还剩下从最后一个标签转移到stop标签的转移得分未计算，同理，这里也不需要计算到stop标签的发射得分(因为实际已经没输入了)。

score += self.end_transitions[last_tags]

用score累加last_tags就好了，这个last_tags如何计算呢

last_tags = tags[-1]

⬆️❌❌⬆️ 注意这种写法是错误的，因为tags中可能包含填充字符，因此正确的做法是通过mask得到有效的最后一个标签：

valid_last_idx = mask.long().sum(dim=0) - 1  # 有效的最后一个索引

这样我们正确得到了最后一个索引，所以last_tags应该是：

last_tags = tags[valid_last_idx, torch.arange(batch_size)]

到此为止，该批次内的两个标签序列的得分已经计算完毕了。

图6

不知道读者有没有感受到这种累加的思想，计算当前时间步的累计得分，只需要前一个时间步的累计得分加上由前一个时间步标签转移到当前时间步标签的得分，最后再加上当前时间步产生当前时间步对应标签的得分即可。

只计算一个标签序列的得分是比较简单的，计算所有可能的标签序列的得分会复杂一些，但是这种累加思想还是一样的。下面就会看到。

计算配分函数

这里的实现需要利用前向算法，每次计算到当前时间步时间步所有标签的累计得分$\alpha$，是一个维度为标签个数的向量，最后汇聚到stop标签时对该向量求和得到一个标量。当然如果考虑批次大小，就得到一个维度为批次大小的向量，该向量的每个元素是该批次内的累计得分。

前向算法这里就不展开了，可以参考统计学习方法——条件随机场。

函数_compute_partition的实现，具体就是实现如下公式：
$$\log \left(\sum _{\tilde{y}\in Y_x}{e}^{s(x,y)}\right)\text{\hspace{1em}(8)}$$
上面已经说过了，这里面包含log-sum-exp的形式。这里会考虑所有可能的标签组合序列，因此该函数对比上面的函数，不需要传入标签序列。

把公式$(3)$代入到公式$(8)$：
$$\log \left(\sum _{\tilde{y}\in Y_x}{e}^{{\sum }_{i=0}^n{A}_{{\tilde{y}}_i,{\tilde{y}}_{i+1}}+{\sum }_{i=1}^n{P}_{i,{\tilde{y}}_i}}\right)\text{\hspace{1em}(9)}$$
得到了一个更清晰的公式。

本小节我们先一步一步分析，最后再给出代码。为了好分析，也基于上小节的例子。

图7

第一步需要计算由start标签，转移到所有标签的得分。即图7上面红框框出来的部分。

 score = self.start_transitions # (num_tags,)

这个start_transitions确实表示的由start标签转移到所有其他标签的得分，标签之间的转移与输入无关。

从上一小节我们知道，下面需要加上由第0个时间步产生所有标签的得分。

来看emissions，它的形状是(seq_len, batch_size, num_tags)，描述的是批次内输入的第几个时间步产生哪个标签的得分。

显然这里seq_len维度的取值为0，表示第0个时间步，后面两个维度不需要指定，代表批次内所有数据以及所有标签。

score = self.start_transitions # (num_tags,)
# (num_tags,) + (batch_size, num_tags)
score += emissions[0]

但是这么写报错了，因为不能自动广播。这里要想自动广播，可以先把start_transitions为形状扩展为(1, num_tags)和(batch_size, num_tags)对应，那么(1, num_tags)就能自动广播成(batch_size, num_tags)。实际上在batch_size维度上复制了batch_size次。

score = start_transitions.unsqueeze(0) # (1, num_tags)
score = score + emissions[0]
score

上面说实际上在第0个维度上复制了batch_size次，下面用代码证实一遍：

可以看到最后输出的结果是一样的，但是显示地进行维度复制很啰嗦，利用自动广播的性质可以帮我们实现。

图8

接下来我们的目标看向第1个时间步的所有标签，即上图框出来的部分。我们要计算前一时间步所有标签的累计得分＋前一个时间步所有标签转移到此时间步所有标签的转移得分＋此时间步上批次内输入产生所有标签的发射得分。

很容易想到的代码是：

score = score + self.transitions + self.emissions[1]

transitions是前一个时间步所有标签转移到当前时间步所有标签的得分，emissions[1]是第1个时间步上批次内的输入产生所有标签的得分。

但它也报错了，因此，我们写上维度：

# (batch_size, num_tags) + (num_tags, num_tags) + (batch_size, num_tags)
score + transitions + emissions[1]

显然它是有问题的，在只有两个维度的情况下是无法相加的，回想下我们的目的是计算批次内上一时间步的所有标签转移到当前时间步的所有标签的得分，根据这段话，我们可以看到三个维度：批次、上一时间步的所有标签、当前时间步的所有标签。因此，如果我们考虑把所有参与计算的部分广播成形状(batch_size, num_tags, num_tags)，是不是就可以相加了。

对于当前时间步1来说，公式$(9)$可以写成：
$$\log \left(\sum _{\tilde{y}\in Y_x}{e}^{A_{{\tilde{y}}_0,{\tilde{y}}_1}+P_{1,{\tilde{y}}_1}}\right)\text{\hspace{1em}(10)}$$
这里用标签对应的索引代表标签，即所有的标签有 { 0 , 1 , 2 , 3 , 4 } \{0,1,2,3,4\} {0,1,2,3,4}，$Y_x$是所有的标签的一个组合：

from itertools import product
import numpy as np

options = np.arange(num_tags)
list(product(options, repeat=2))

所有的$Y_x$如上所示，其中当然包括很多不符合BIO规范的组合。

我们这一步实际上要计算：
$$\log \left(\sum _{\tilde{y}\in Y_x}{e}^{A_{{\tilde{y}}_0,{\tilde{y}}_1}+P_{1,{\tilde{y}}_1}}\right)=\log \left(\underset{\text{所有标签到标签0}}{\underbrace{e^{A_{0,0}+P_{1,0}}+e^{A_{1,0}+P_{1,0}}+e^{A_{2,0}+P_{1,0}}+e^{A_{3,0}+P_{1,0}}+e^{A_{4,0}+P_{1,0}}}}+\underset{\text{所有标签到标签1}}{\underbrace{e^{A_{0,1}+P_{1,1}}+e^{A_{1,1}+P_{1,1}}+e^{A_{2,1}+P_{1,1}}+e^{A_{3,1}+P_{1,1}}+e^{A_{4,1}+P_{1,1}}}}+\underset{\text{所有标签到标签4}}{\underbrace{\cdots +e^{A_{4,4}+P_{1,4}}}}\right)\text{\hspace{1em}(11)}$$
在前向算法的过程中，实际上是得到一个向量，即到此时间步为止所有标签上的累计得分$\alpha$。

如果展开的话，即
$$\left[\begin{array}{c}\log (e^{A_{0,0}+P_{1,0}+\text{score}}+e^{A_{1,0}+P_{1,0}+\text{score}}+e^{A_{2,0}+P_{1,0}+\text{score}}+e^{A_{3,0}+P_{1,0}}+e^{A_{4,0}+P_{1,0}+\text{score}})\\ \log (e^{A_{0,1}+P_{1,1}+\text{score}}+e^{A_{1,1}+P_{1,1}+\text{score}}+e^{A_{2,1}+P_{1,1}+\text{score}}+e^{A_{3,1}+P_{1,1}}+e^{A_{4,1}+P_{1,1}+\text{score}})\\ \log (e^{A_{0,2}+P_{1,2}+\text{score}}+e^{A_{1,2}+P_{1,2}+\text{score}}+e^{A_{2,2}+P_{1,2}+\text{score}}+e^{A_{3,2}+P_{1,2}}+e^{A_{4,2}+P_{1,2}+\text{score}})\\ \log (e^{A_{0,3}+P_{1,3}+\text{score}}+e^{A_{1,3}+P_{1,3}+\text{score}}+e^{A_{2,3}+P_{1,3}+\text{score}}+e^{A_{3,3}+P_{1,3}}+e^{A_{4,3}+P_{1,3}+\text{score}})\\ \log (e^{A_{0,4}+P_{1,4}+\text{score}}+e^{A_{1,4}+P_{1,4}+\text{score}}+e^{A_{2,4}+P_{1,4}+\text{score}}+e^{A_{3,4}+P_{1,4}}+e^{A_{4,4}+P_{1,4}+\text{score}})\end{array}\right]\text{\hspace{1em}(12)}$$
这里$P_{1,0}$表示第1个时间步产生标签0的得分，$P_{1,1}$表示第1个时间步产生标签1的得分。

即我们计算的结果是图8中红框框出来的那5个标签对应的向量，形状是(num_tags)，如果考虑批次的话，形状就是(batch_size, num_tags)。和我们在第0个时间步上计算出来的score形状一致。

回到上面的代码，我们说要把参与计算的部分广播成形状(batch_size, num_tags, num_tags)，表示批次batch_size内从前一个时间步所有num_tags个标签转移到当前时间步所有num_tags个标签的得分。

我们先把score的维度扩展一下：

score.unsqueeze(2).shape

broadcast_score = score.unsqueeze(2).repeat_interleave(repeats=num_tags, dim=2)

看一下它的变化：

此时相当于沿着维度2复制了5次。

再扩充transitions的维度，回顾下它的形状：(num_tags, num_tags) ，那么只需要在前面插入一个维度，并复制batch_size次即可：

broadcast_transitions = transitions.unsqueeze(0).repeat_interleave(repeats=batch_size, dim=0)

最后扩充emissions的维度，它是时间步相关的，此时考虑的是时间步1的输入，因此我们要看emissions[1]的形状：(batch_size, num_tags)，我们要插入前一个时间步维度，因此：

broadcast_emissions = emissions[1].unsqueeze(1).repeat_interleave(repeats=num_tags, dim=1)

然后把扩充后的相加，得到new_score：

# 形状 (batch_size, num_tags, num_tags)
new_score = broadcast_score + broadcast_transitions + broadcast_emissions 

得到的new_score形状是(batch_size, num_tags, num_tags) 。表示批次batch_size内每个样本从前一个时间步所有num_tags个标签转移到当前时间步所有num_tags个标签的得分。即new_score[0,1,2]表示批次内第0个样本从前一时间步第1个标签转移到当前时间步第2个标签的得分。在仅考虑1个样本的情况下，实际上得到的是下面这个矩阵(未考虑前一时间步的累计得分)：
$$\left[\begin{array}{ccccc}{A}_{0,0}+P_{1,0}& A_{0,1}+P_{1,1}& A_{0,2}+P_{1,2}& A_{0,3}+P_{1,3}& A_{0,4}+P_{1,4}\\ A_{1,0}+P_{1,0}& A_{1,1}+P_{1,1}& A_{1,2}+P_{1,2}& A_{1,3}+P_{1,3}& A_{1,4}+P_{1,4}\\ A_{2,0}+P_{1,0}& A_{2,1}+P_{1,1}& A_{2,2}+P_{1,2}& A_{2,3}+P_{1,3}& A_{2,4}+P_{1,4}\\ A_{3,0}+P_{1,0}& A_{3,1}+P_{1,1}& A_{3,2}+P_{1,2}& A_{3,3}+P_{1,3}& A_{3,4}+P_{1,4}\\ A_{4,0}+P_{1,0}& A_{4,1}+P_{1,1}& A_{4,2}+P_{1,2}& A_{4,3}+P_{1,3}& A_{4,4}+P_{1,4}\end{array}\right]$$
new_score[0,3,2]就是下图红框框出来的时间步：

表示$A_{3,2}+P_{1,2}$，即由第3个标签转移到第2个标签 ＋ 当前时间步产生第2个标签的得分。

看起来不过，我们通过矩阵运算一次计算出了所有的结果，但如何确定这个结果是正确的。

为了方便，我们下面只考虑一个输入，即第0个输入。重新回顾下上面的广播。

先看上一步计算的累计score：

如上图所示，我们只考虑橙色框起来的那个输入。里面的值用不同颜色的字体进行了解释，橙色框中矩阵的每行值都是一样的，表示都是前一个时间步(所有标签)到(当前时间步)某个标签的(累计)得分。

再看转移得分transitions：

它们两相加：

这里描述了上述矩阵两个元素：

• 前一时间步第0个标签到当前时间步第0个标签的转移得分 ＋前一个时间步所有标签到当前时间步第0个标签的累计得分

• 前一时间步第4个标签到当前时间步第2个标签的转移得分 ＋前一个时间步所有标签到当前时间步第2个标签的累计得分

下面就剩下发射得分了：

我们用前面计算的结果和它相加：

即得到的new_score形状是(batch_size, num_tags, num_tags) 。表示批次batch_size内每个样本从前一个时间步所有num_tags个标签转移到当前时间步所有num_tags个标签的得分。即new_score[0,1,2]表示批次内第0个样本从前一时间步第1个标签转移到当前时间步第2个标签的得分。

图9

即此时我们得到了图9红框框出来的这样一个矩阵，下面我们要汇聚到当前位置上，可以通过求和即可。

把公式$(12)$拷贝下来：
$$\left[\begin{array}{c}\log (e^{A_{0,0}+P_{1,0}+\text{score}}+e^{A_{1,0}+P_{1,0}+\text{score}}+e^{A_{2,0}+P_{1,0}+\text{score}}+e^{A_{3,0}+P_{1,0}}+e^{A_{4,0}+P_{1,0}+\text{score}})\\ \log (e^{A_{0,1}+P_{1,1}+\text{score}}+e^{A_{1,1}+P_{1,1}+\text{score}}+e^{A_{2,1}+P_{1,1}+\text{score}}+e^{A_{3,1}+P_{1,1}}+e^{A_{4,1}+P_{1,1}+\text{score}})\\ \log (e^{A_{0,2}+P_{1,2}+\text{score}}+e^{A_{1,2}+P_{1,2}+\text{score}}+e^{A_{2,2}+P_{1,2}+\text{score}}+e^{A_{3,2}+P_{1,2}}+e^{A_{4,2}+P_{1,2}+\text{score}})\\ \log (e^{A_{0,3}+P_{1,3}+\text{score}}+e^{A_{1,3}+P_{1,3}+\text{score}}+e^{A_{2,3}+P_{1,3}+\text{score}}+e^{A_{3,3}+P_{1,3}}+e^{A_{4,3}+P_{1,3}+\text{score}})\\ \log (e^{A_{0,4}+P_{1,4}+\text{score}}+e^{A_{1,4}+P_{1,4}+\text{score}}+e^{A_{2,4}+P_{1,4}+\text{score}}+e^{A_{3,4}+P_{1,4}}+e^{A_{4,4}+P_{1,4}+\text{score}})\end{array}\right]$$

可以看到每项都包含log-sum-exp的形式，而Pytorch已经实现了log-sum-exp，所以有：

# new_score = broadcast_score + broadcast_transitions + broadcast_emissions
# (batch_size, num_tags, num_tags) -> ((batch_size, num_tags))
new_score = torch.logsumexp(new_score, dim=1) 
new_score

实际计算为：

这样，我们计算到了第1个时间步处的$\alpha$，即这里的new_score：

图10

但，别忘了，还可能是填充，因此还要乘以考虑mask，这里用torch.where实现：

mask = torch.ByteTensor([[1,1],[1,1],[1,1],[1,0],[1,0]])
score = torch.where(mask[1].bool().unsqueeze(1), new_score, score)
score

由于当前时间步还没有填充，因此结果不变。

torch.where(condition, input, other)当condition为真，则取input，否则取other。它是按元素取值的。这里先把mask[1]转换成bool。

这样，当前时间步的$\alpha$算是计算完成了，以此类推，直到计算了最后一个时间步，得到了：

图11

别忘了，还有最后一个时间步所有标签转移到end标签的得分加上score向量的每个分量，相当于：
$$\log \left(\sum _{\tilde{y}\in Y_x}{e}^{A_{{\tilde{y}}_0,{\tilde{y}}_1}+P_{1,{\tilde{y}}_1}}\right)=\log \left(e^{A_{0,n}+{\text{score}}_0}+e^{A_{1,n}+{\text{score}}_1}+e^{A_{2,n}+{\text{score}}_2}+e^{A_{3,n}+{\text{score}}_3}+e^{A_{4,n}+{\text{score}}_4}\right)\text{\hspace{1em}(12)}$$
可以看到又有一个log-sum-exp，因此我们的代码就可以写成：

# (batch_size,)
end_transitions = torch.randn(num_tags)
# (batch_size, num_tags) + (batch_size,) 会发生自动广播
# (batch_size, num_tags)
score += end_transitions
# (batch_size, num_tags) ->(batch_size,)
score = torch.logsumexp(score, dim=1)

这样就通过前向算法计算出了批次内每个样本的规划化因子，即累计得分，对于每个样本来说，都是一个标量。

最后给出该函数的代码：

def _compute_partition(
    self, emissions: torch.Tensor, mask: torch.ByteTensor
) -> torch.Tensor:
    """利用CRF的前向算法计算partition的分数

    Args:
        emissions (torch.Tensor): 发射分数P 形状 (seq_len, batch_size, num_tags)
        mask (torch.ByteTensor): 表明哪些元素为填充符  (seq_len, batch_size)

    Returns:
        torch.Tensor: 批次内的partition分数 形状(batch_size,)
    """

    seq_len = emissions.shape[0]
    # score (batch_size, num_tags) 对于每个批次来说，第i个元素保存到目前为止以i结尾的所有可能序列的得分
    score = self.start_transitions.unsqueeze(0) + emissions[0]

    for i in range(1, seq_len):
        # broadcast_score: (batch_size, num_tags, 1) = (batch_size, pre_tag, current_tag)
        # 所有可能的当前标签current_tag广播
        broadcast_score = score.unsqueeze(2)
        # 广播成 (batch_size, 1, num_tags)
        # shape: (batch_size, 1, num_tags)
        broadcast_emissions = emissions[i].unsqueeze(1)
        # (batch_size, num_tags, num_tags) = (batch_size, num_tags, 1) + (num_tags, num_tags) + (batch_size, 1, num_tags)
        current_score = broadcast_score + self.transitions + broadcast_emissions
        # 在前一时间步标签上求和  -> (batch_size, num_tags)
        # 对于每个批次来说，第i个元素保存到目前为止以i结尾的所有可能标签序列的得分
        current_score = torch.logsumexp(current_score, dim=1)
        # mask[i].unsqueeze(1) -> (batch_size, 1)
        # 只有mask[i]是有效标签的current_score才将值设置到score中，否则保持原来的score
        score = torch.where(mask[i].bool().unsqueeze(1), current_score, score)

    # 加上到end标签的转移得分 end_transitions本身保存的是所有的标签到end标签的得分
    # score (batch_size, num_tags)
    score += self.end_transitions
    # 在所有的标签上求(logsumexp)和
    # return (batch_size,)
    return torch.logsumexp(score, dim=1)

此时我们可以利用pytorch提供的优化算法，基于带标签的数据集训练这个CRF模型了。

假设在训练好模型后，进行进行预测呢？请看下篇文章。

---

下一篇： 一文弄懂条件随机场(下)

---

参考

1. 统计学习方法——条件随机场
2. pytorch-crf
3. ADVANCED: MAKING DYNAMIC DECISIONS AND THE BI-LSTM CR
4. 《统计学习方法》——隐马尔可夫模型