1. 题目

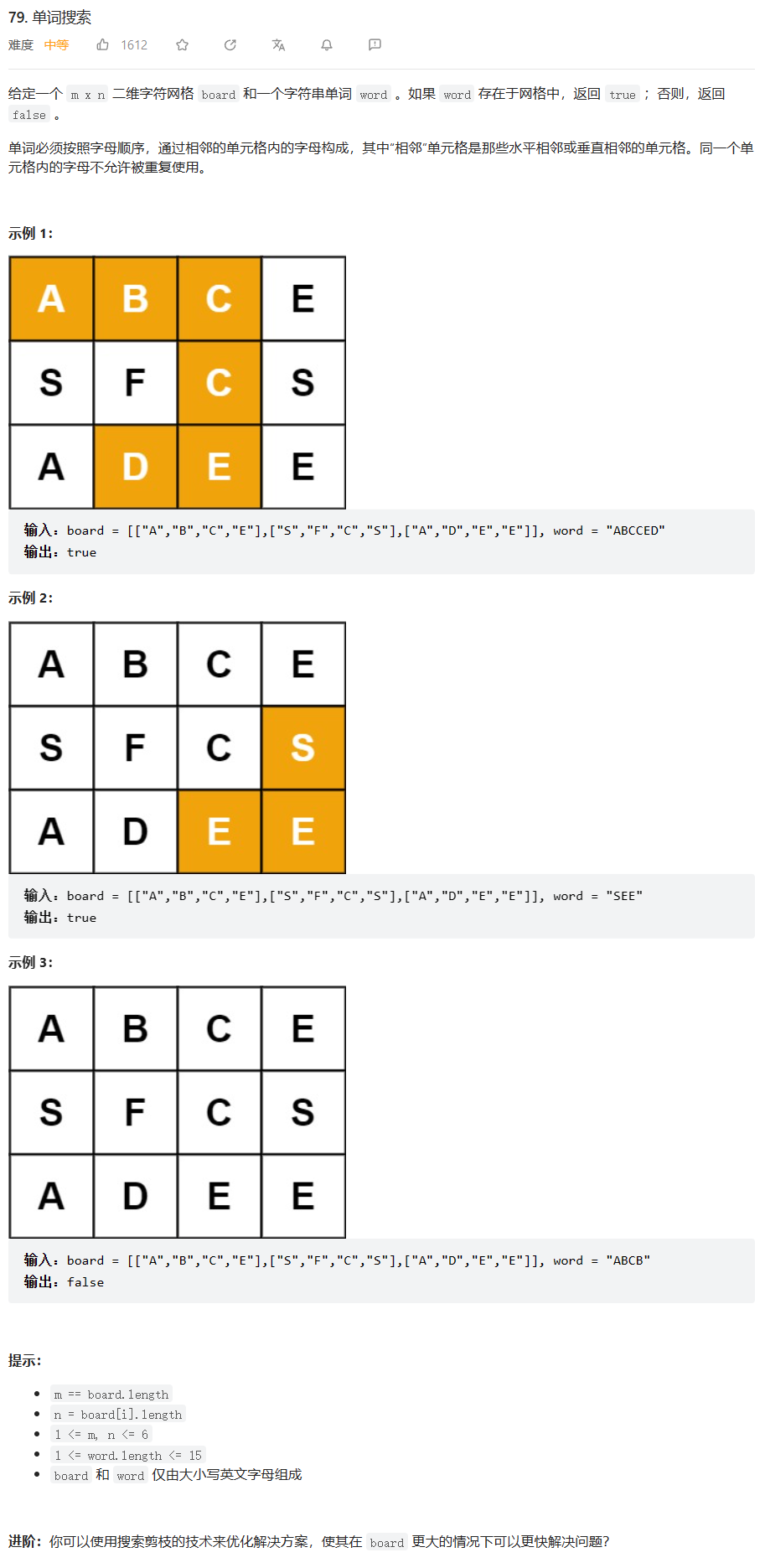
LeetCode 剑指 Offer II 003. 前 n 个数字二进制中 1 的个数

1.1 题意

计算 0 到 n 之间的每个数的二进制表示中 1 的个数

1.2 分析

看时间复杂度，O(32n)应该能过（也就是每个数一位一位去数1的个数），知道low-bit这个运算x & (x-1) 的话时间复杂度肯定低于O(32n)，具体复杂度参考题解是O(nlogn)。

0 <= n <= 10e5

但是查看底下数据范围的时候，有一个进阶提示，可以使用O(n)，好家伙一下子来了兴致。
于是我列出了几行找规律。
在这里插入图片描述
发现规律了嘛？每一行，把他从中间对半分成两份，前面一份，刚巧是上一行的结果，后面一份是前面一份的结果+1。

        2^0: 1
        2^1: 1 | 2
        2^2: 1 2 | 2 3
        2^3: 1 2 2 3 | 2 3 3 4
        ......

why? 因为下一行的前半份最高位为1，次高位为0，上一行中对应的最高位为0，次高位为1，所以他们1的个数会相同；对于下一行中后半份，最高位和次高位都为1，所以后半分是前半份的结果+1。

举个例子可能更能明白（另一个情况同理举例即可，主要是帮助理解）：

    			2^2: 1 2 2 3
	   对应的10进制: 4 5 6 7
        		2^3: 1 2  2  3  2  3  3  4
	   对应的10进制: 8 9 10 11 12 13 14 15
	   举例4，5和8，9：
	   		4，5对应的二进制为0100 0101
	   		8，9对应的二进制为1000 1001
	   =>下一行的前半份最高位为1，次高位为0，上一行中对应的最高位为0，次高位为1

那接下来写递推式（具体细节可以看代码，主要是清楚这个规律，得到递推）：
对于前半段，从上一行抄下来： $res[2^i+j]=res[2^{(i-1)} + j]$
对于后半段，从前半段抄下来并+1： $res[2^i + j + 2^{(i-1)}]=res[2^i+j]+1$

细节上注意边界情况。

1.3 我的解法

class Solution {
public:
    vector<int> countBits(int n) {
        // 0000 0001 0010 0011 0100 0101 0110 0111 1000
        //    0    1    2    3    4    5    6    7    8
        //    0    1    1    2    1    2    2    3    1

        // 2^0: 1
        // 2^1: 1 2
        // 2^2: 1 2 2 3
        // 2^3: 1 2 2 3 2 3 3 4
        // ......
        if(n == 0){
            return {0};
        }
        vector<int> res;
        res.emplace_back(0);
        res.emplace_back(1);

        for(int i=1; i<=( log(n)/log(2) ); i++){
            int num = pow(2,i);
            for(int j=0; j<num/2 && ( (1<<i)+j <= n ); j++){
                // ind: 2^i+j
                // copy from  2^(i-1) + j
                res.emplace_back(res[(1 << (i-1)) + j]);
            }
            for(int j=0; j<num/2 && ( ( (1<<i) + j + (1<<(i-1)) ) ) <= n ; j++){
                // ind: 2^i + j + 2^(i-1)
                // copy from: 2^i+j
                res.emplace_back(res[(1 << i) + j] + 1);
            }
        }
        return res;
    }
};