定积分是微积分的一种应用,通过定积分可以求出曲线下面的面积、弧长、质心、转动惯量等一系列物理量。以下是定积分的一些常见应用:
-
曲线下面的面积:定积分可以用于求曲线下面的面积。举个例子,如果想要求函数f(x) = x^2在区间[0,1]上的面积,可以将[0,1]等分成n个小区间,然后计算每个小区间上矩形的面积之和,当n趋近于无穷大时,这个和就趋近于函数在区间[0,1]上的曲线下面积。
-
弧长:定积分可以用于计算曲线的弧长。举个例子,如果想要求函数f(x) = x^(3/2)在区间[0,1]上的弧长,可以使用下面的公式计算:
L = ∫[0,1] √(1+(f’(x))^2) dx
其中f’(x)是函数f(x)的导数。
- 质心:定积分可以用于计算曲线的质心。举个例子,如果想要求函数f(x) = x^2在区间[0,1]上的质心,可以使用下面的公式计算:
x = (1/A)∫[0,1] x*f(x) dx
y = (1/A)∫[0,1] f(x) dx
其中A是曲线的面积。
- 转动惯量:定积分可以用于计算物体的转动惯量。举个例子,如果想要求一个半径为r、密度为ρ的球的转动惯量,可以使用下面的公式计算:
I = ∫∫∫ r^2 ρ sin(θ) dr dθ dφ
其中r、θ、φ分别是球坐标系下的径向、极角和方位角,ρ是球的密度。
定积分的应用-元素法
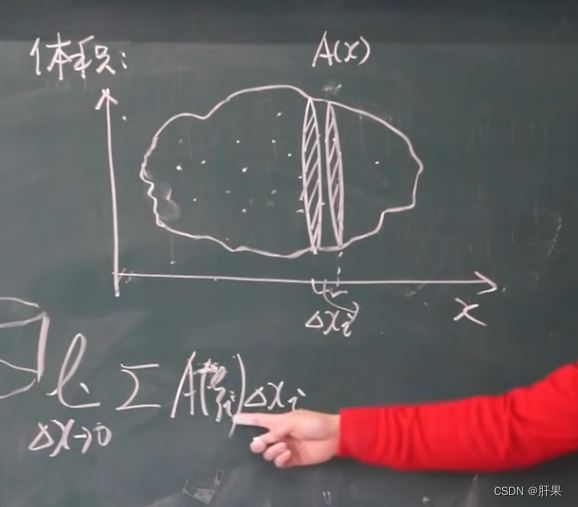
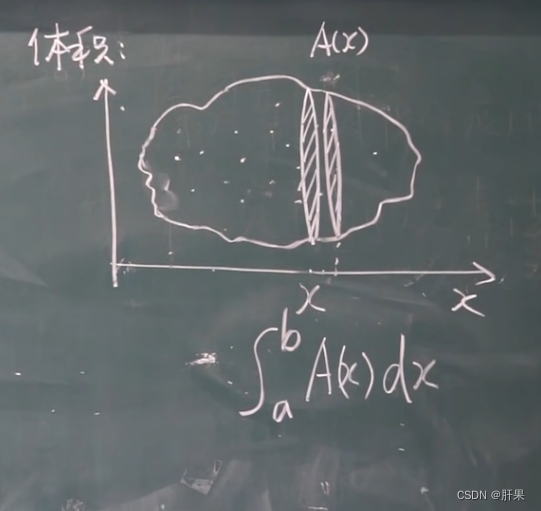
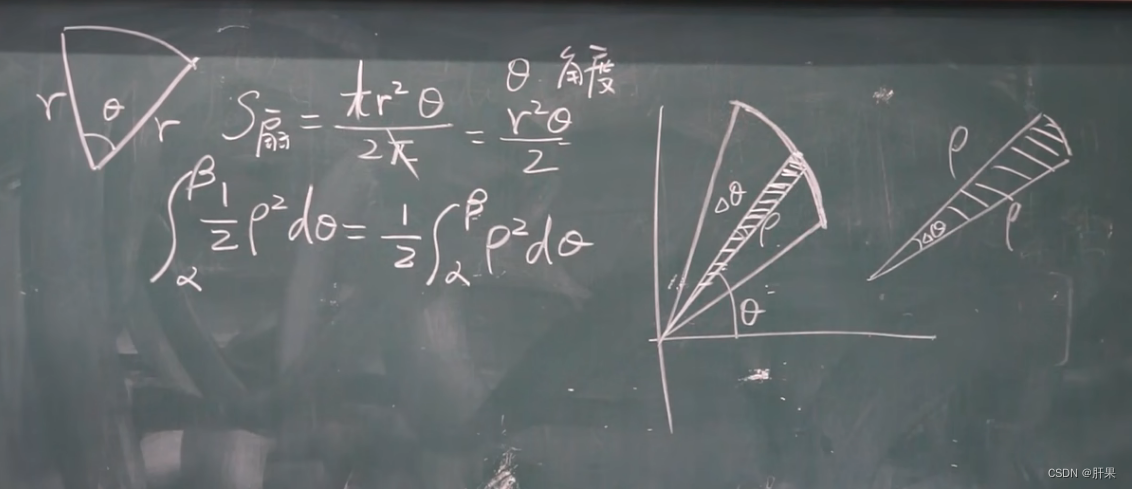
定积分的应用-求面积
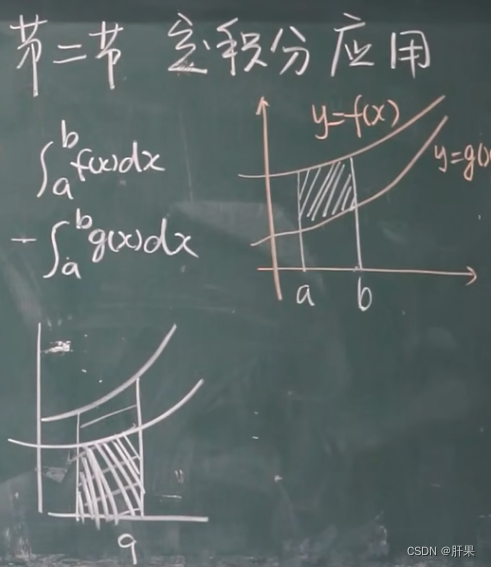


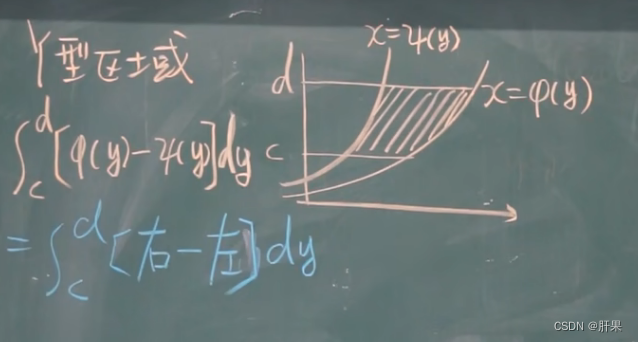
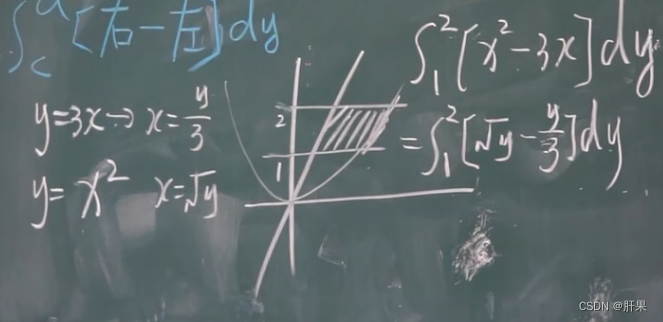

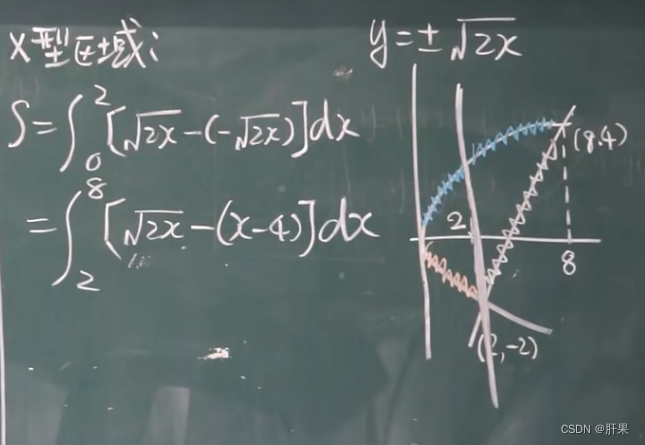
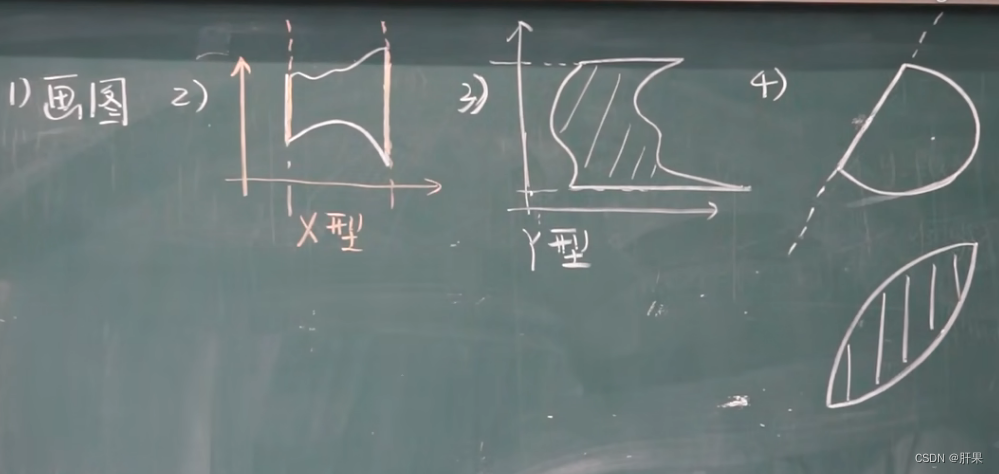
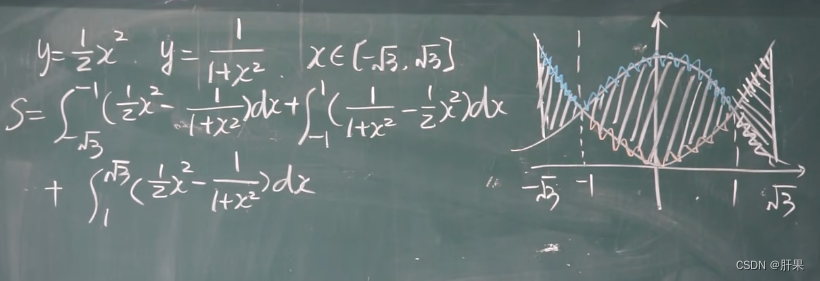
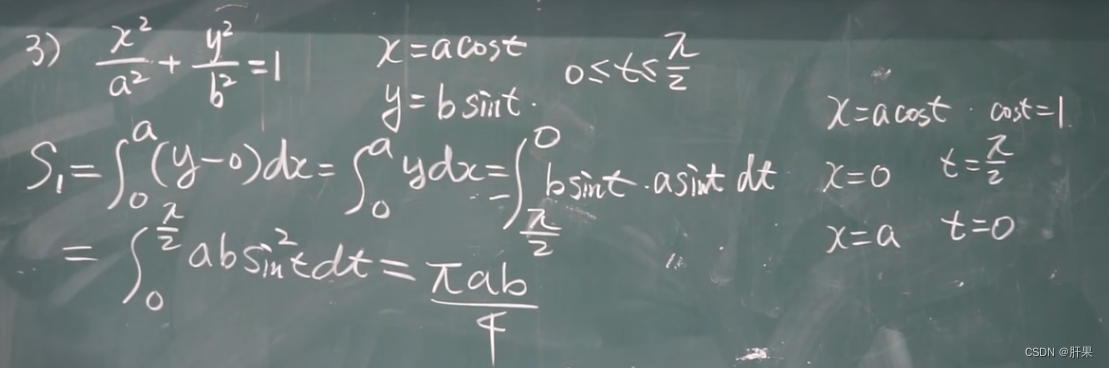

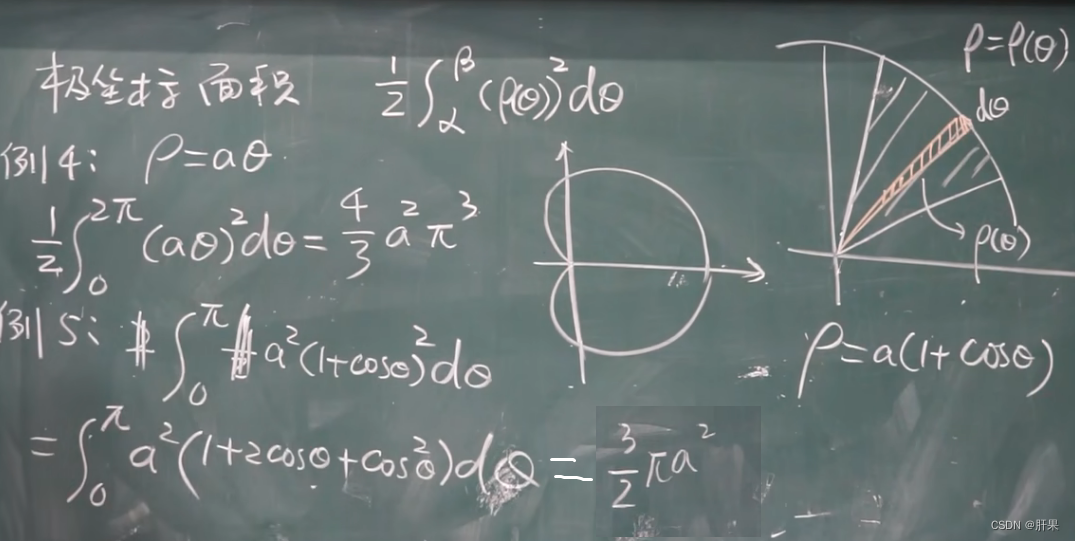
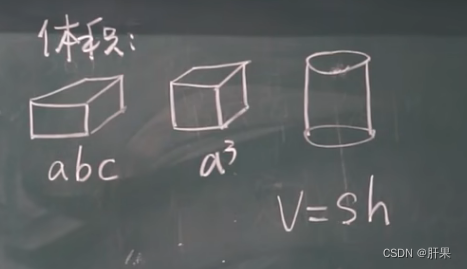
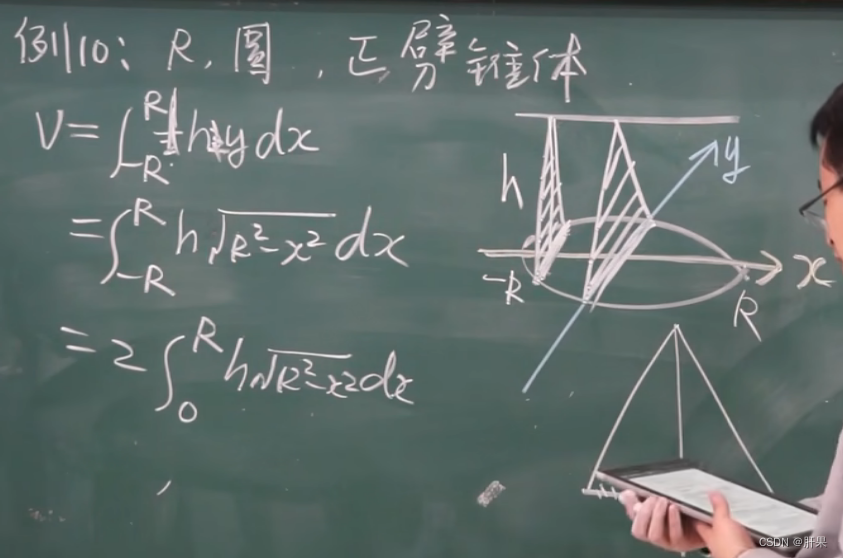
旋转体体积

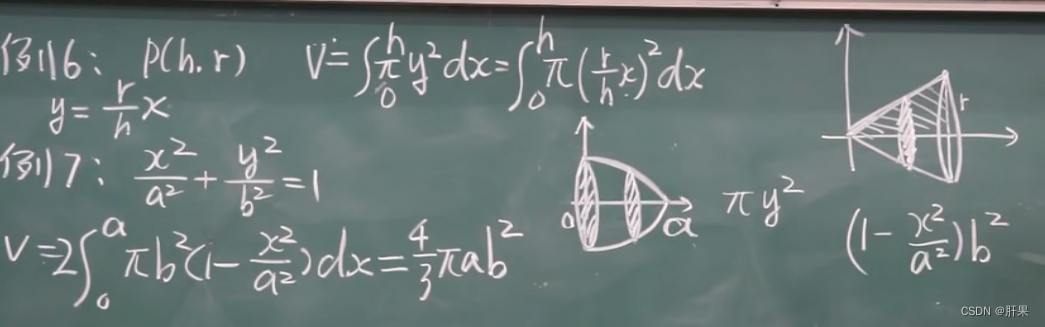
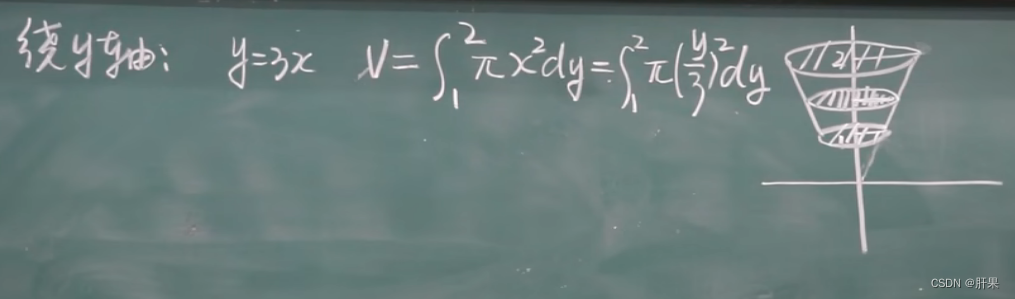
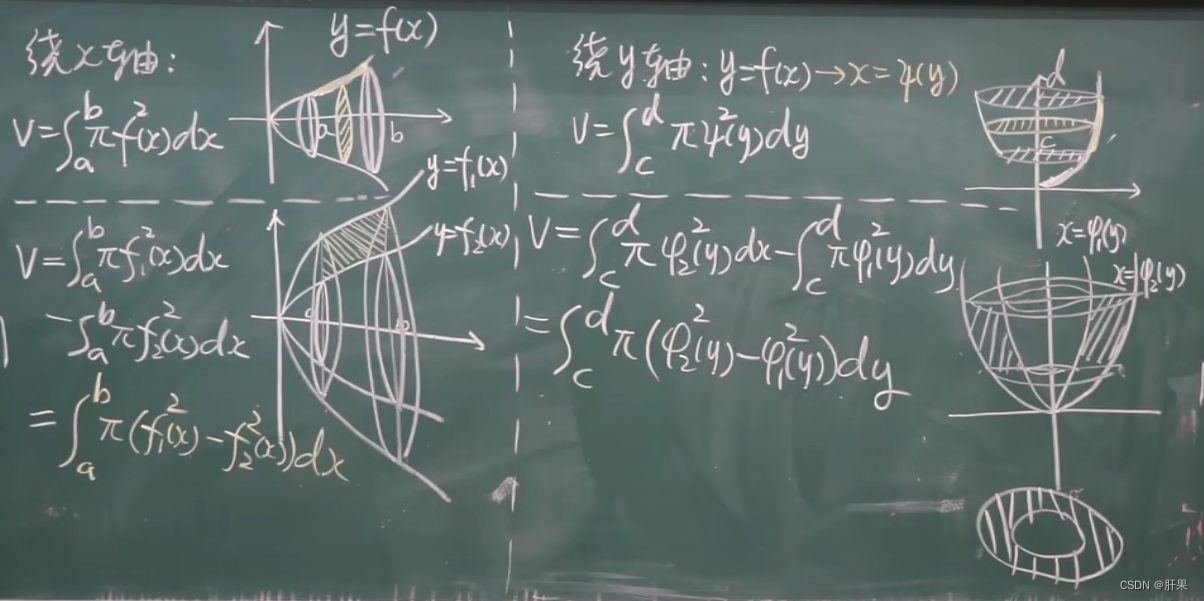

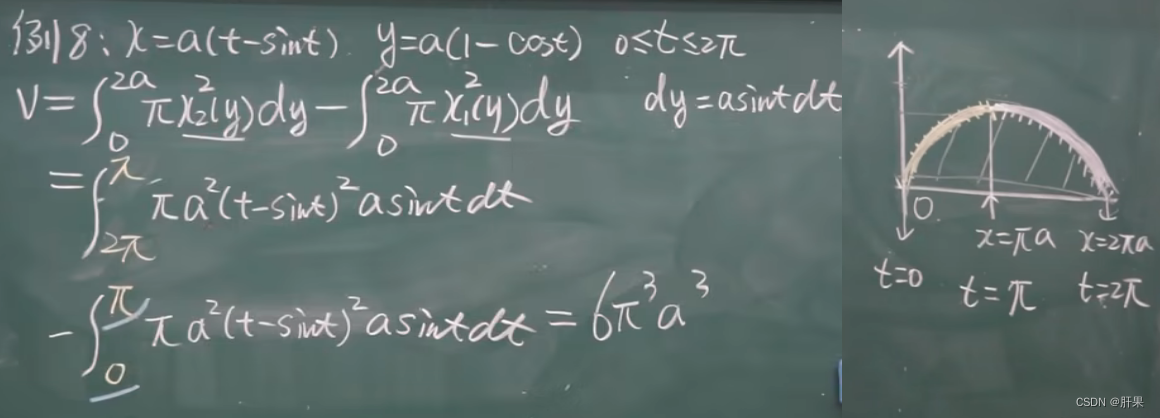

弧长公式
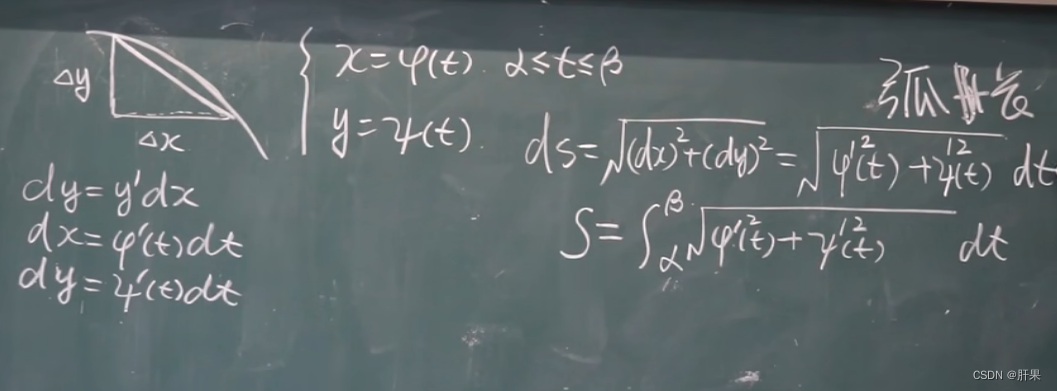

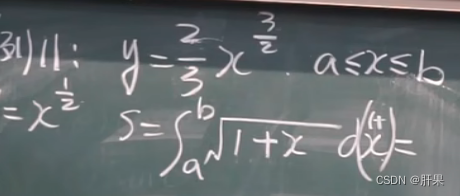
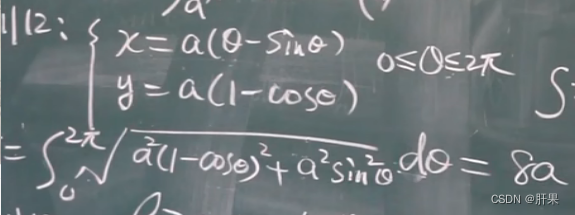
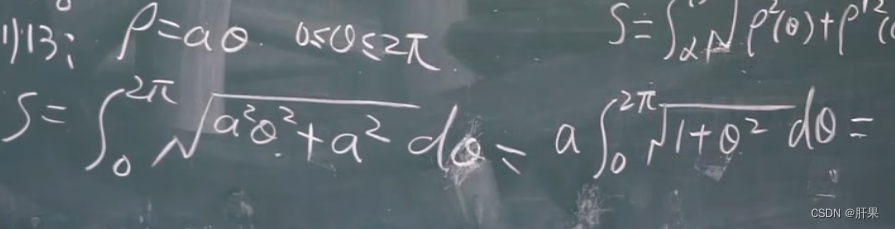
定积分在物理学上的应用


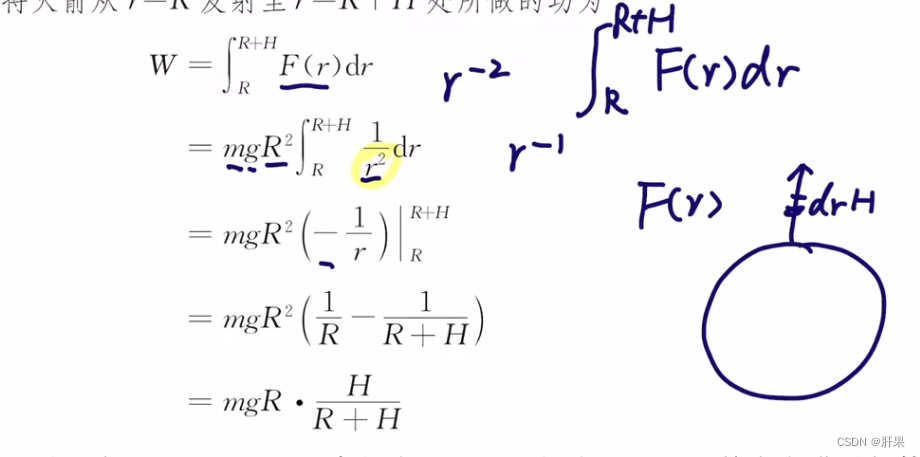





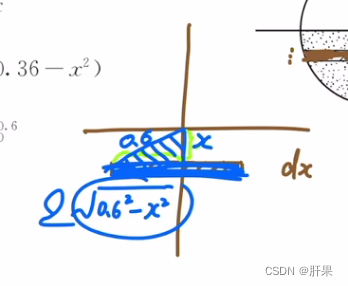



定积分在物理学中有多个应用,以下是一些常见的应用:
-
将曲线下的面积作为速度或加速度函数的时间积分
在物理学中,速度和加速度是非常重要的物理量,通过测量并对其进行积分可以得到位移和速度。因此,通过将速度或加速度函数的时间积分,可以得到物体的位移和速度,定积分可以用来计算这一过程中的面积。 -
计算质量、密度、电量、电荷密度等物理量
在物理学中,质量、密度、电量和电荷密度等物理量通常要用积分的形式来计算。这些物理量在空间中通常是连续变化的,而定积分可以将这种连续的变化分割成较小的部分进行计算。 -
计算弧长、曲率和面积等几何量
在物理学中,例如质点在曲线上运动的问题时,弧长和曲率是计算所需的重要几何量。用定积分可以计算弧长和曲率,从而得到所需的物理量。同时,定积分还可以计算曲线下的面积,这在测定物体的体积或是质量时至关重要。 -
计算各类能量
物理学中各种规律的表达式中,往往会出现物理量乘以其变化量积分的形式。例如,功和势能可以用定积分进行计算。在热力学领域中,熵、热容和热力学势等也可以用定积分计算得到。