定义

计算机科学中，递归是一种解决计算问题的方法，其中解决方案取决于同一类问题的更小子集
递归是一种非常高效、简洁的编码技巧，一种应用非常广泛的算法。

如求100以内的和
那么就等同于求100+99以内的和
99以内和等同于99+98以内的和
…
依次类推

注意点

• 递归一定要有出口，不然会死循环
• 警惕堆栈溢出
  当数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

Exception in thread "main" java.lang.StackOverflowError

• 减少重复计算
  如计算100!+99!+…+1的时候
  每次不要都从1开始进行求阶乘，记得存储结果减少重复计算。
  如求100!直接使用$a[99]\ast 100$。(a在算99!的时候求解后存储在其中)

例题

反向打印字符串

public static void reversePrint(String str, int index) {
    if (index == str.length()) {
        return;
    }
    reversePrint(str, index + 1);
    System.out.println(str.charAt(index));
}

斐波那契数列

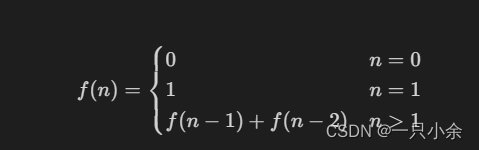
public static int f(int n) {
    if (n == 0) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
    return f(n - 1) + f(n - 2);
}

时间复杂度

$$T(n)=aT(\frac{n}{b})+f(n)$$
其中

• $T(n)$ 是问题的运行时间，$n$ 是数据规模
• $a$ 是子问题个数
• $T(\frac{n}{b})$ 是子问题运行时间，每个子问题被拆成原问题数据规模的 $\frac{n}{b}$
• $f(n)$ 是除递归外执行的计算

令 $x={\log }_{b}a$，即 $x={\log }_{子问题缩小倍数}子问题个数$

那么
$$T(n)=\{\begin{array}{ll}\Theta (n^x)& f(n)=O(n^c)并且c<x\\ \Theta (n^x\log n)& f(n)=\Theta (n^x)\\ \Theta (n^c)& f(n)=\Omega (n^c)并且c>x\end{array}$$

如

$T(n)=T(\frac{7n}{10})+n$

• $a=1,b=\frac{10}{7},x=0,c=1$
• 此时 $x=0<1$，由后者决定整个时间复杂度 $\Theta (n)$