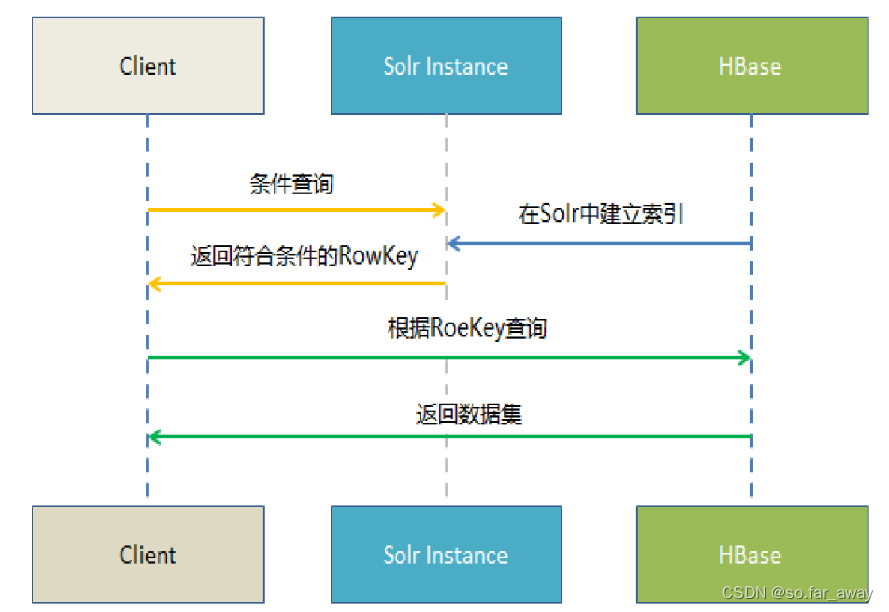
动态查找表
- 1.二叉排序树
- 1.1. 定义
- 1.2. 查找过程
- 1.3. 插入过程
- 1.4. 创建二叉排序树
- 1.5. 删除操作
- (1)被移除的结点是叶子结点
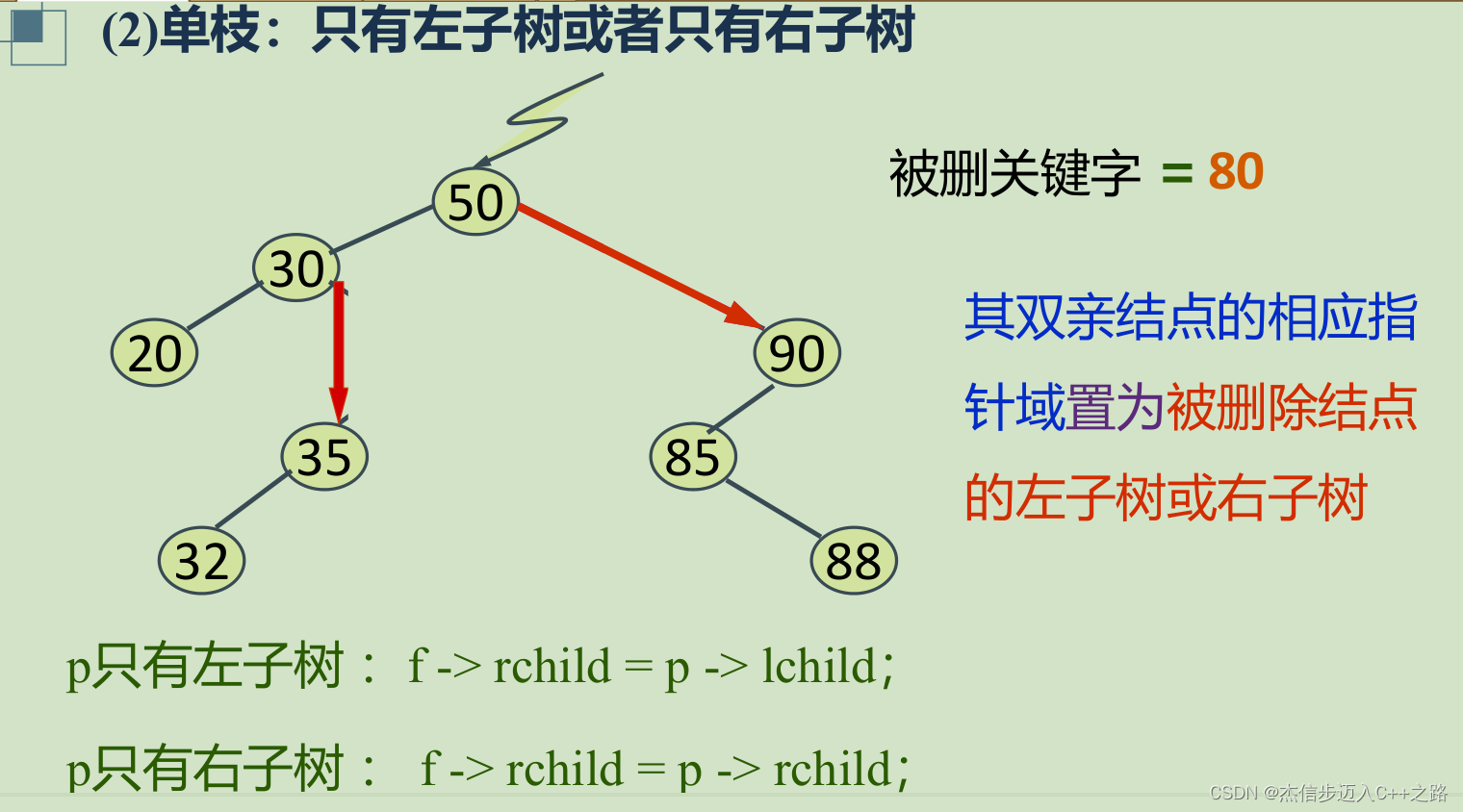
- (2)被移除的结点只有左子树或者只有右子树;
- (3)被移除的结点既有左子树,也有右子树。
- 1.6 性能分析
- 2.平衡二叉树
- 2.1 定义
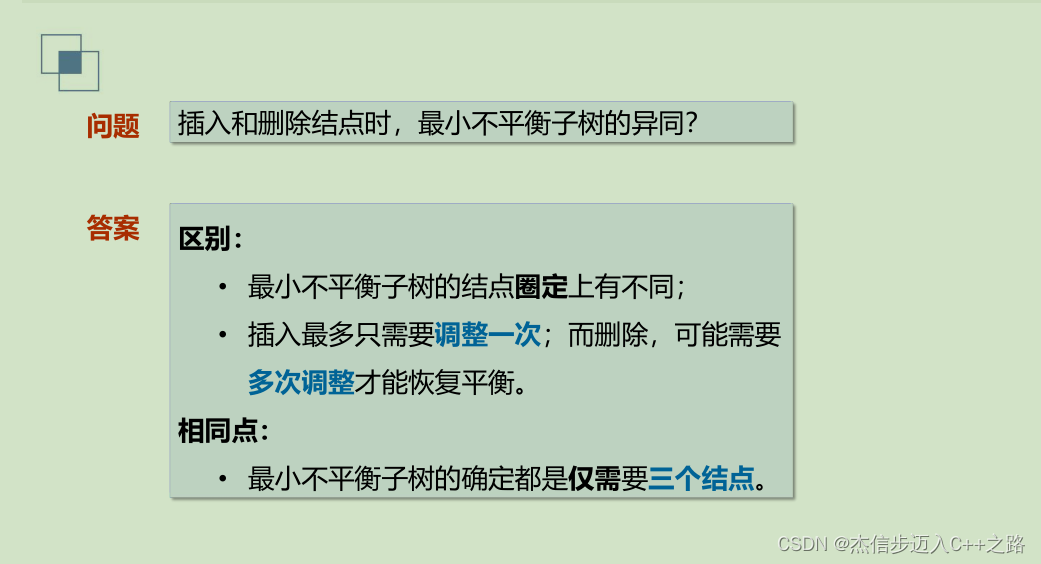
- 2.2. 插入时的最小不平衡子树
- 2.3. 最小不平衡子树调整类型
- LL型
- RR型
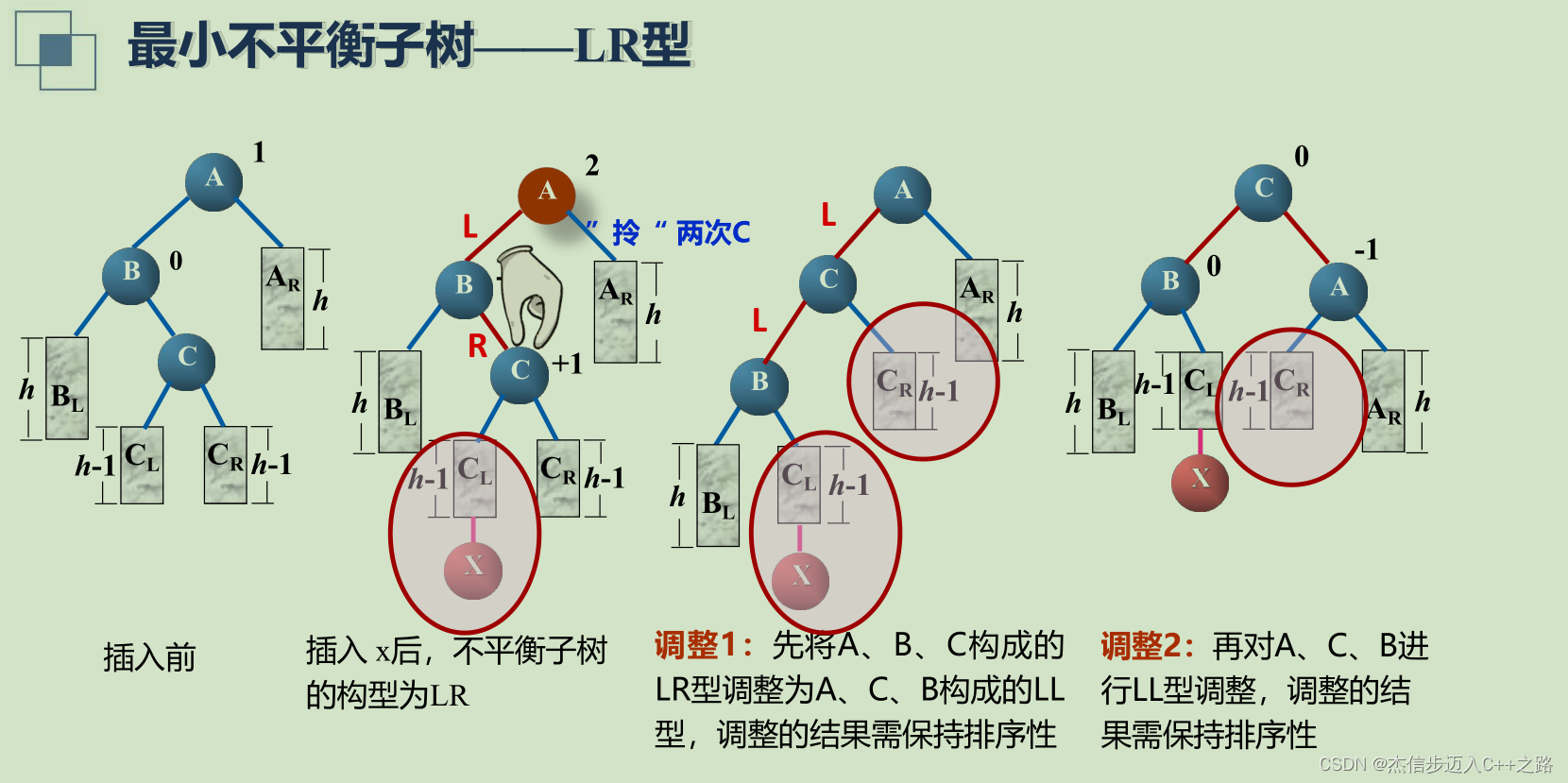
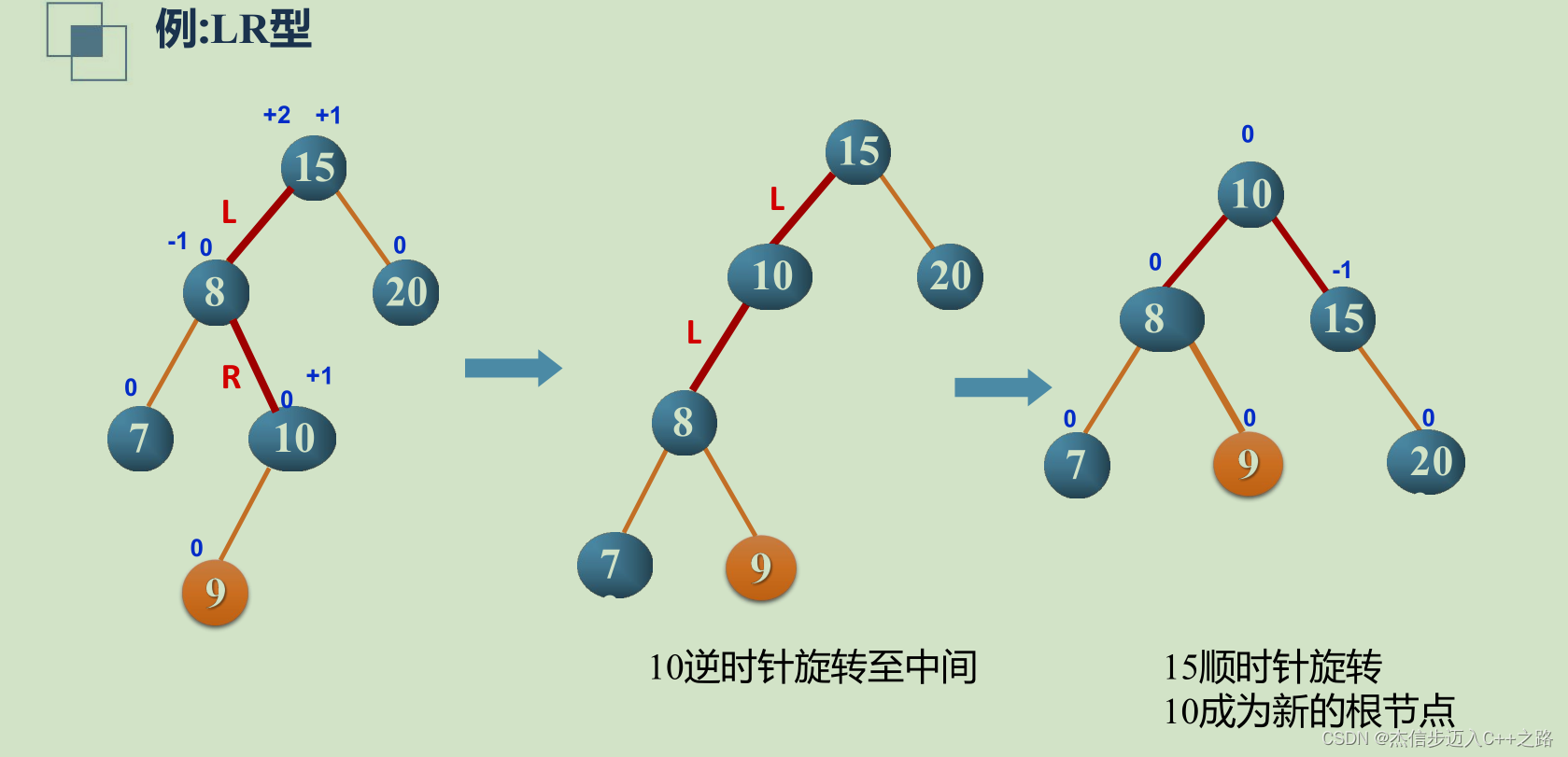
- LR型
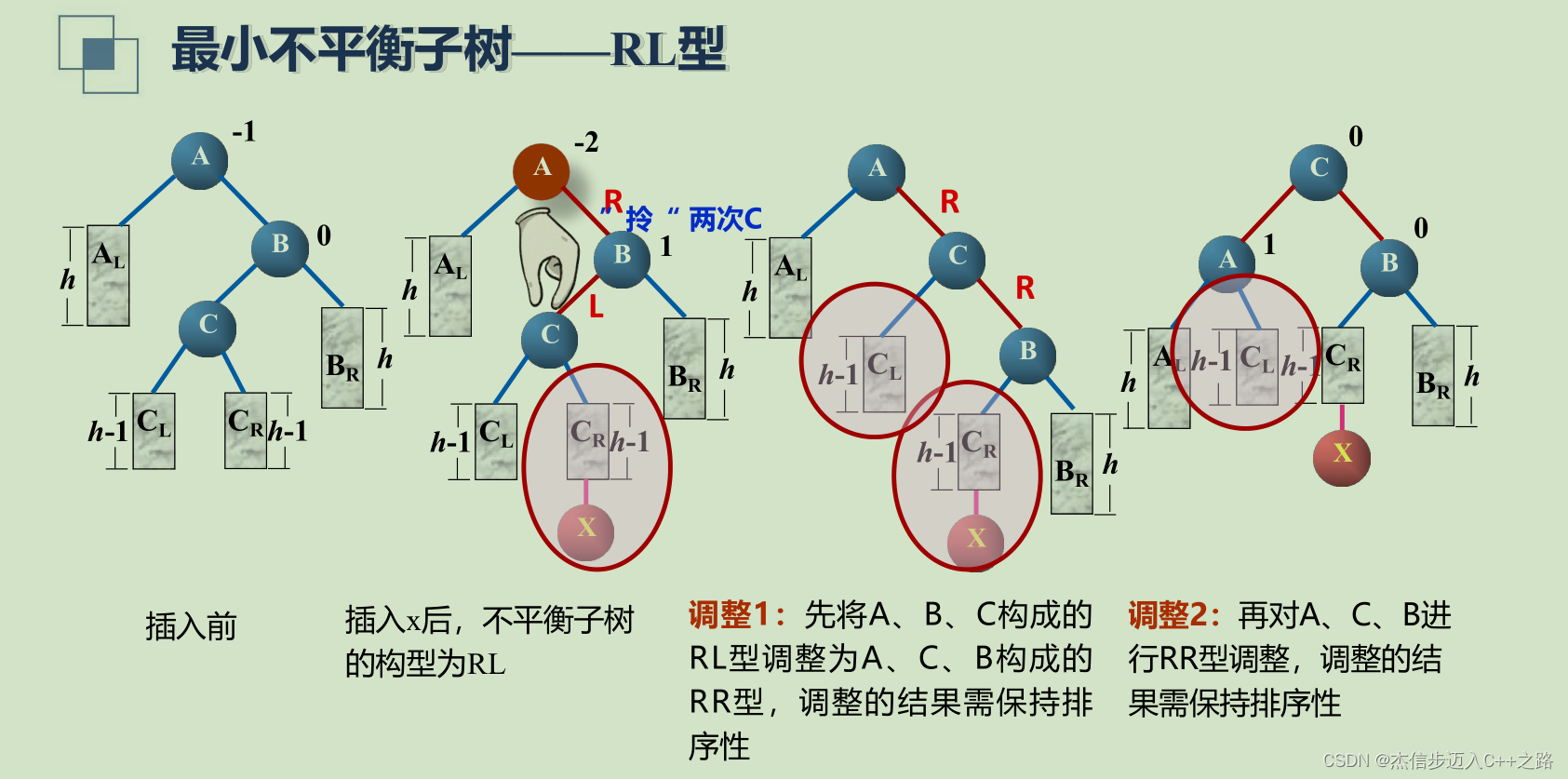
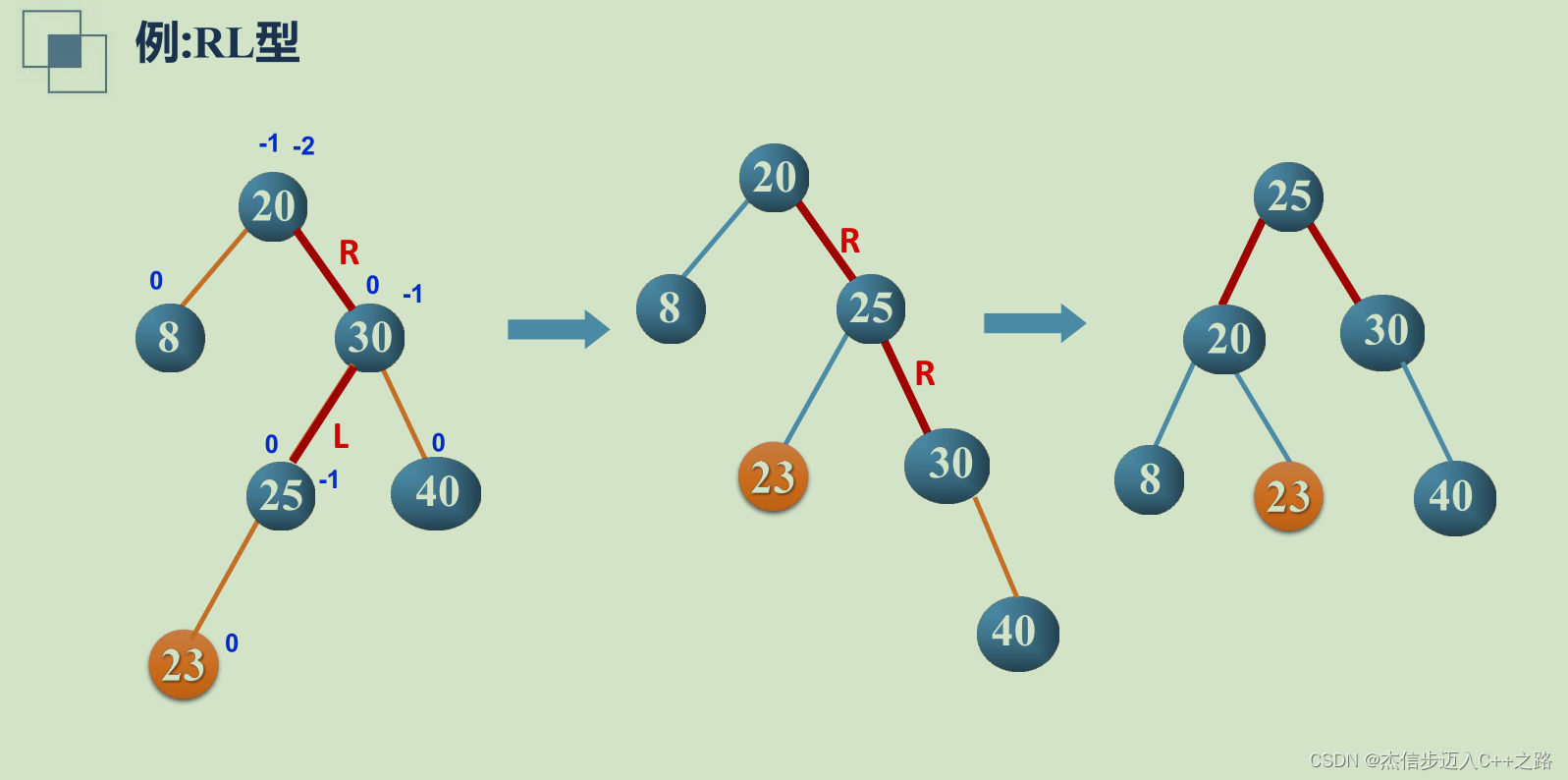
- RL型
- 2.4 平衡二叉树的查找分析
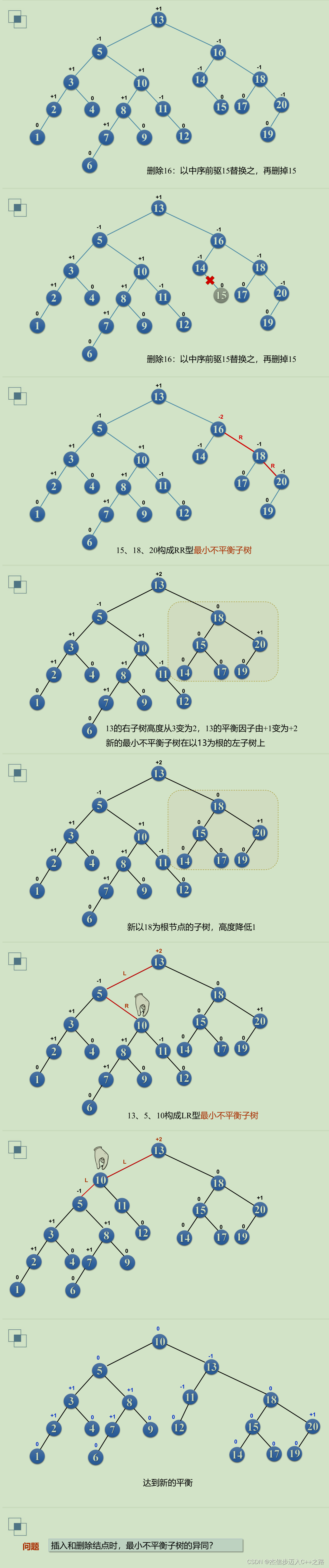
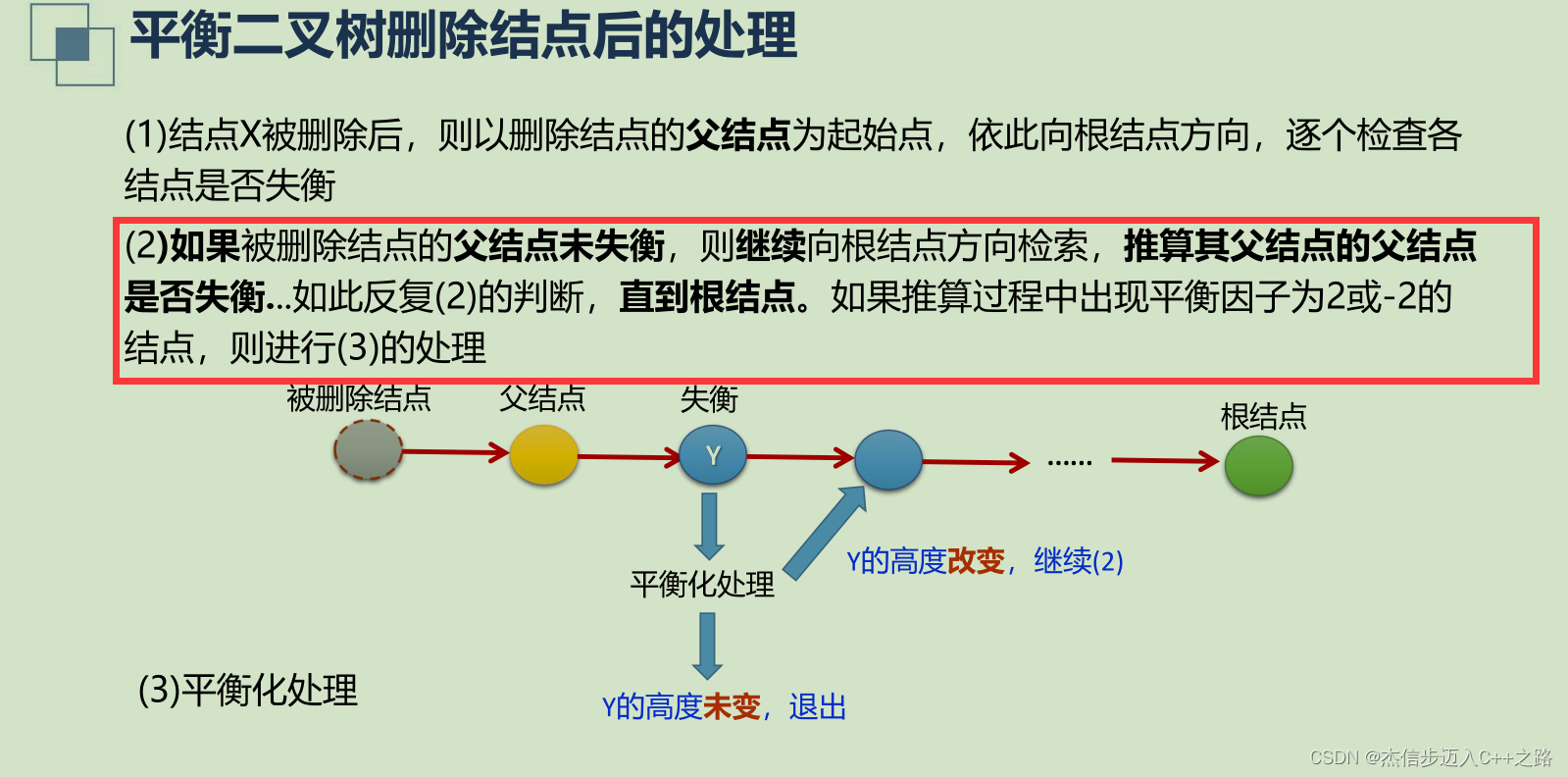
- 2.5 平衡二叉树的结点删除
- 平衡二叉树删除结点后的处理
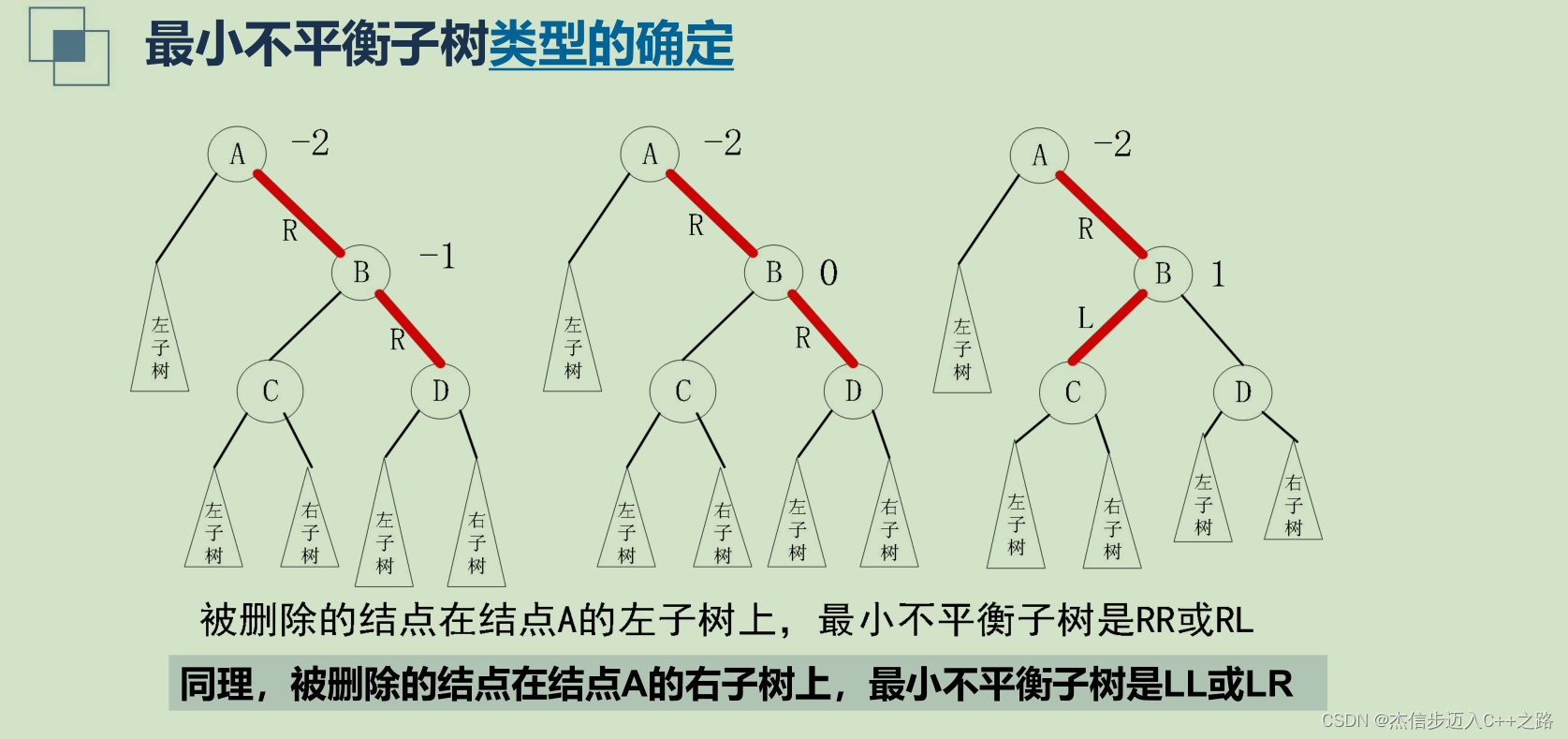
- 最小不平衡子树类型的确定

1.二叉排序树
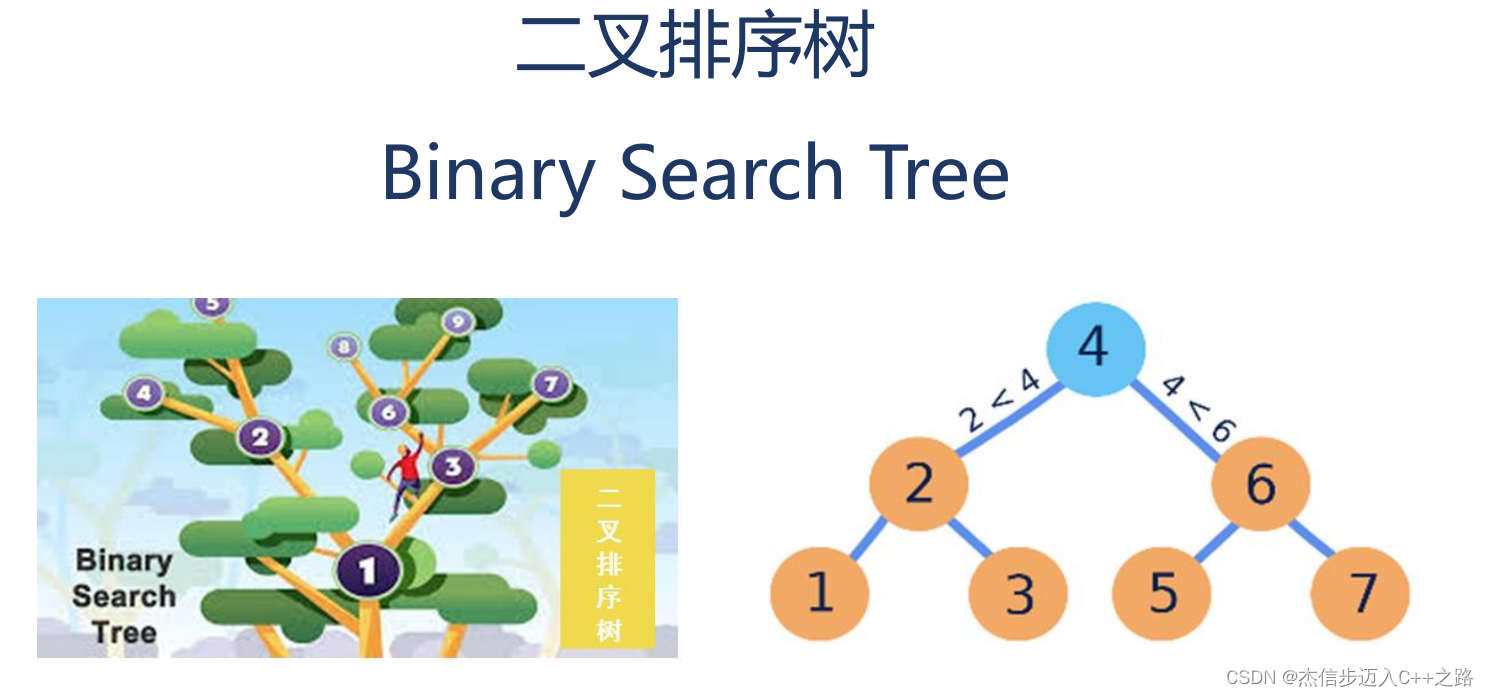
1.1. 定义
或者是一棵空树;或者是具有如下特性的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于根结点的值;
- 它的左、右子树也都分别是二叉排序树。
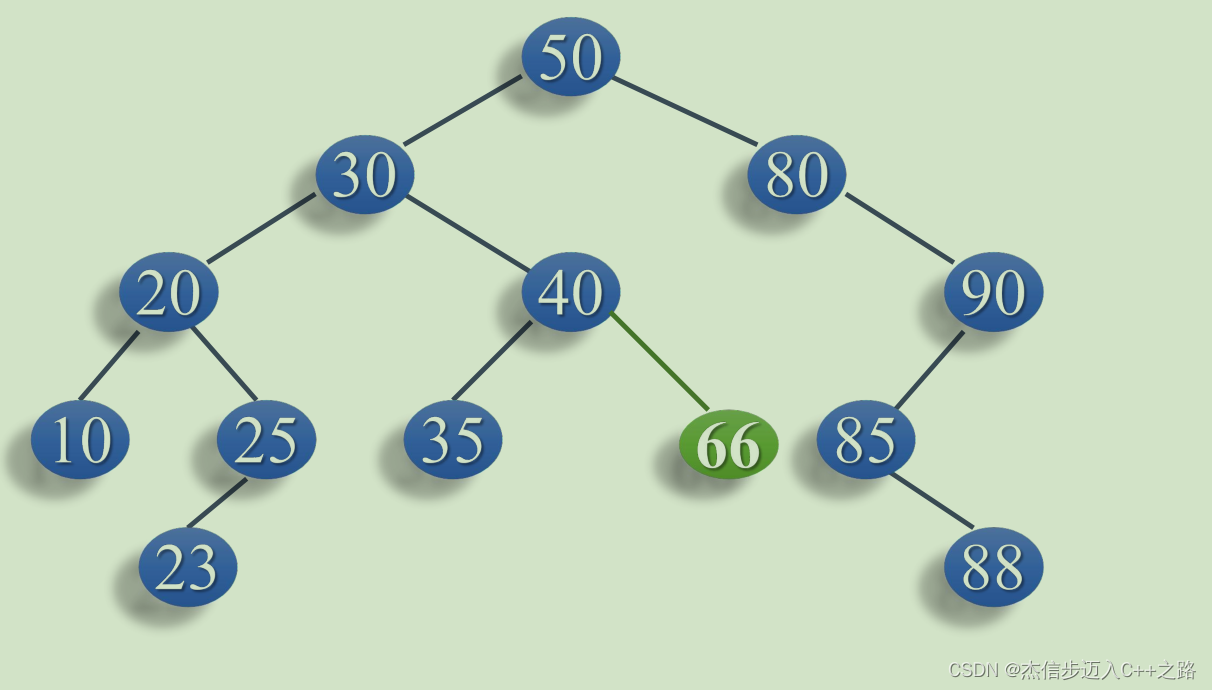
二叉排序树的中序序列是一个有序的序列
1.2. 查找过程
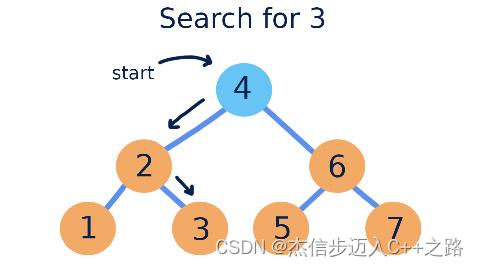
在查找过程中,逐步缩小查找范围的过程,并生成了一条查找路径
【算法描述】
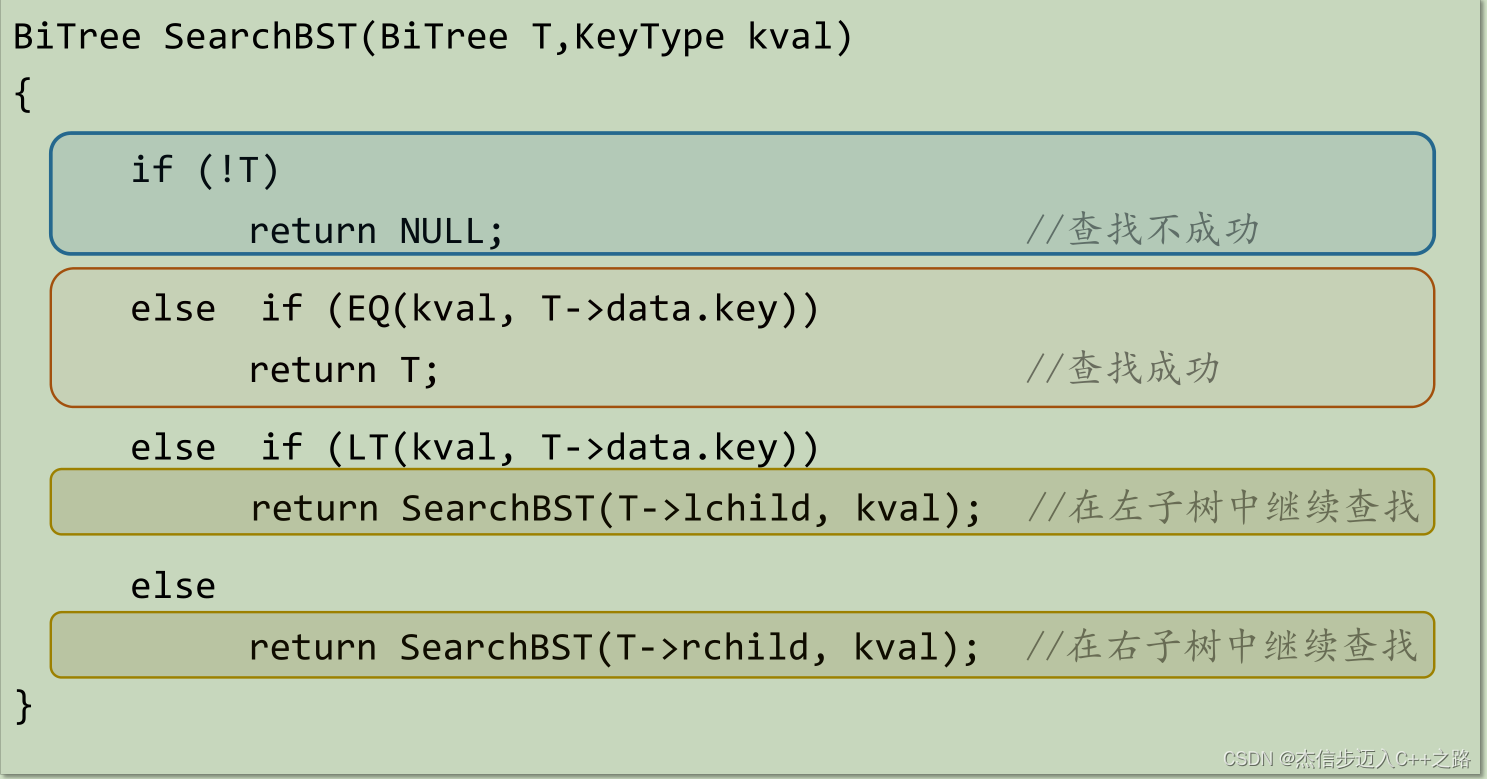
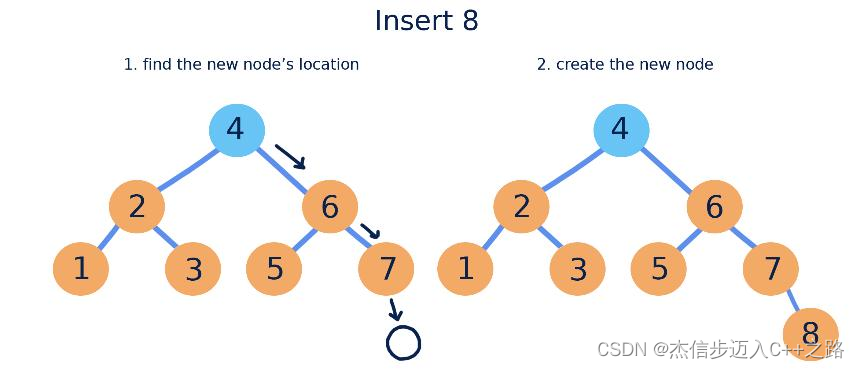
1.3. 插入过程
- 插入的结点只能是叶子结点
- 插入是基于查找失败情况下插入的
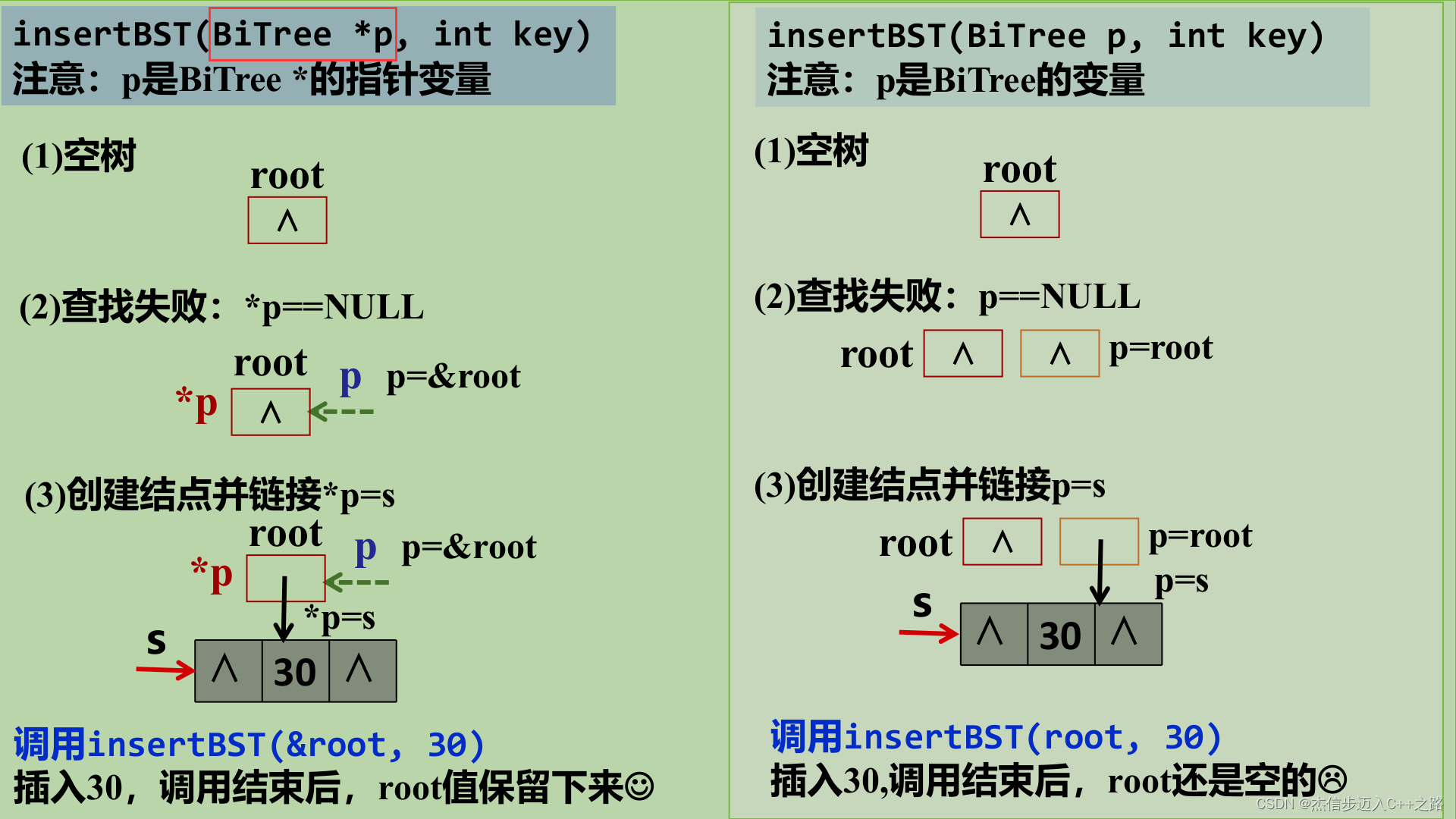
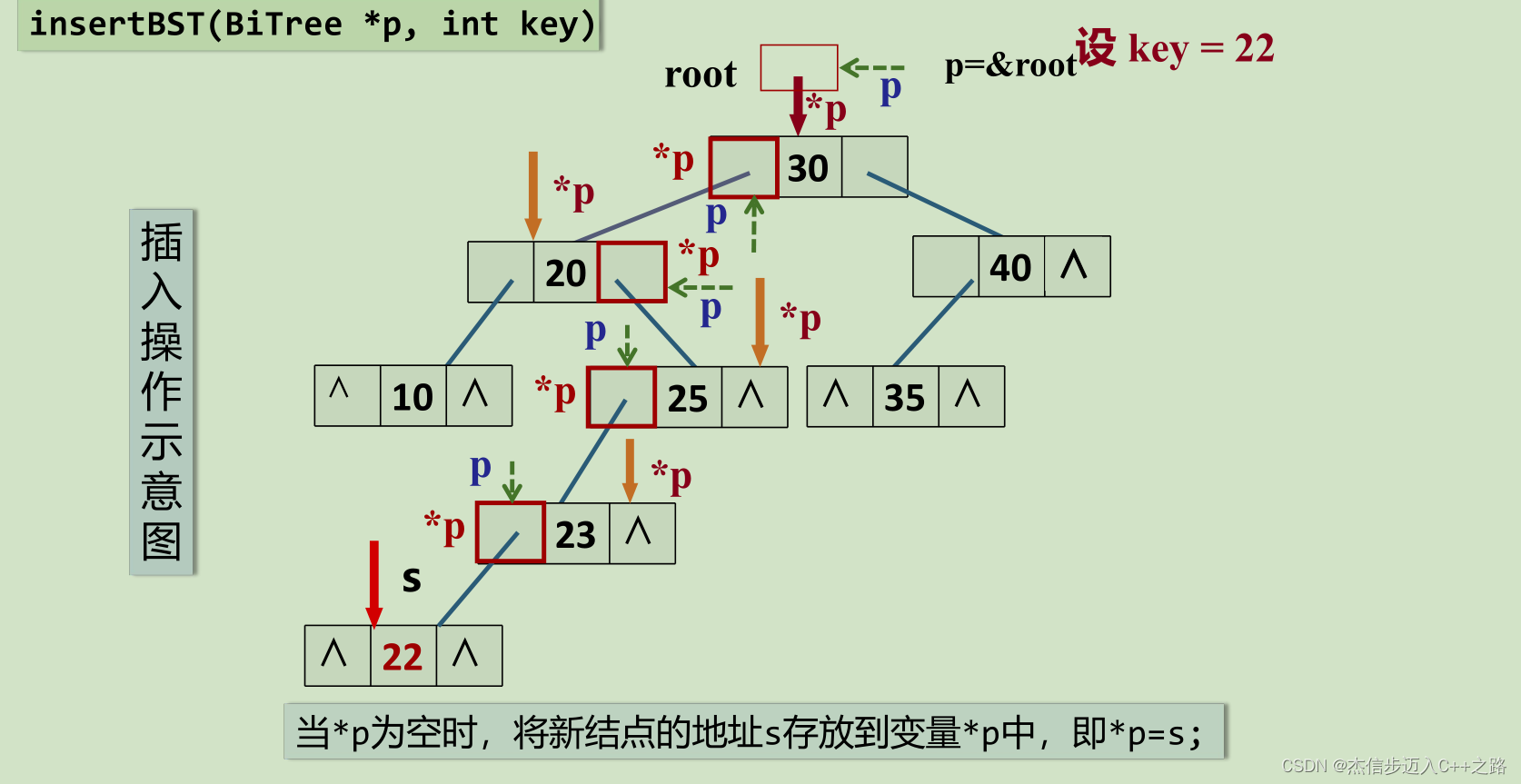
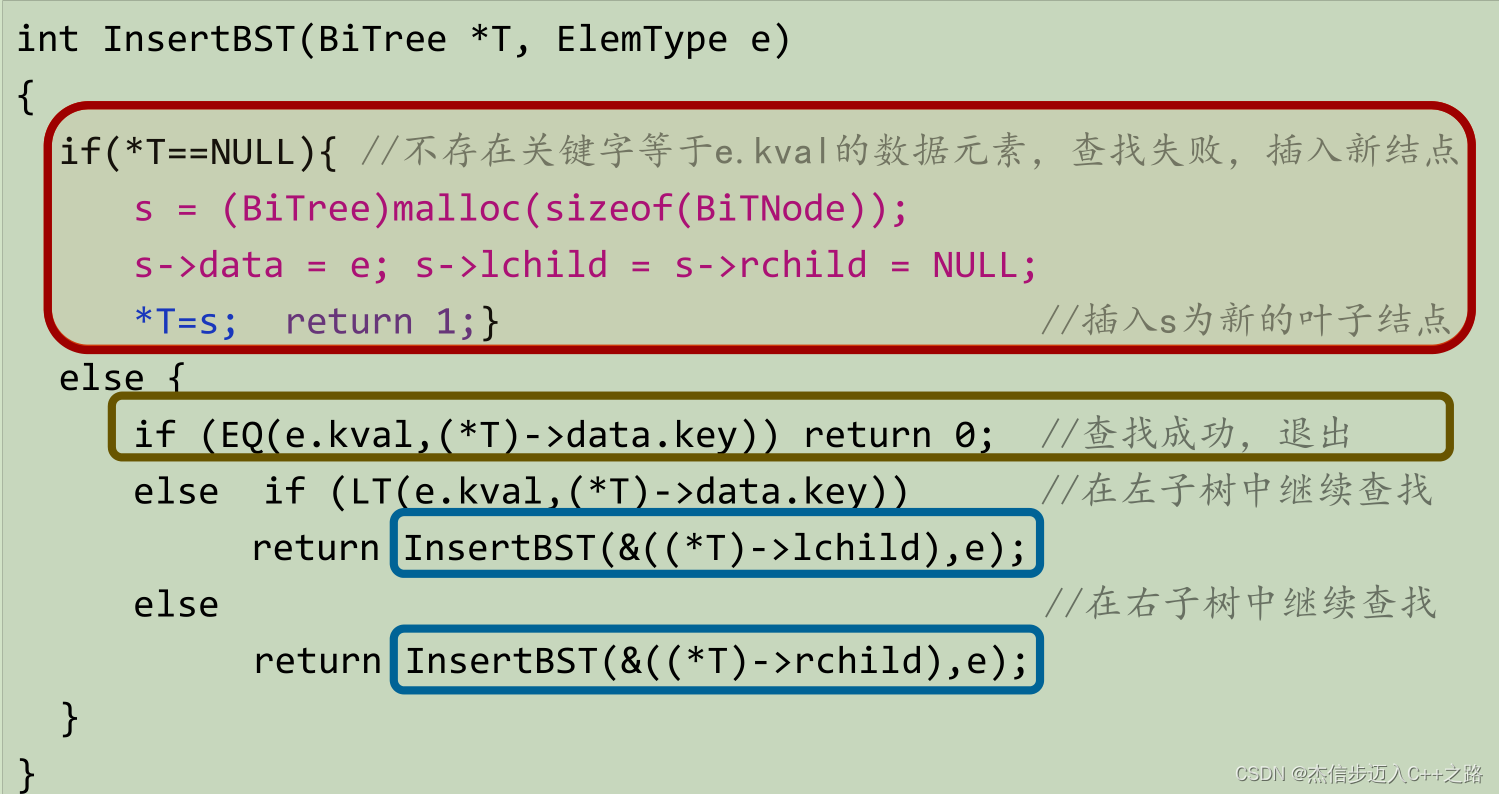
当二叉排序树为空时,插入操作会改变指向根结点的指针,所以p是BiTree *类型的,*p是p指向的对象。
1.4. 创建二叉排序树
二叉排序树在查找的过程中从无到有,动态生成
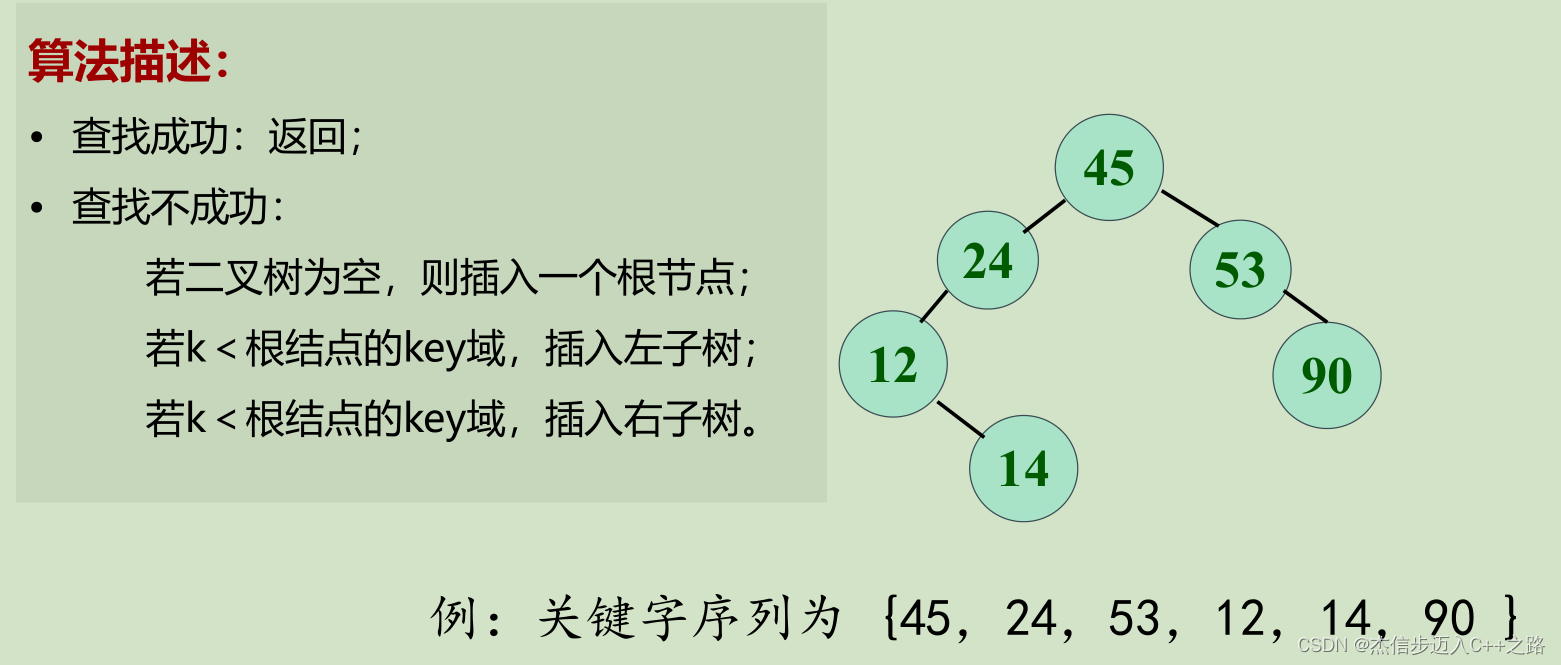
【插入算法】

【创建算法】

1.5. 删除操作
要求: 确保移除之后,依然保持排序
存在三种情况:
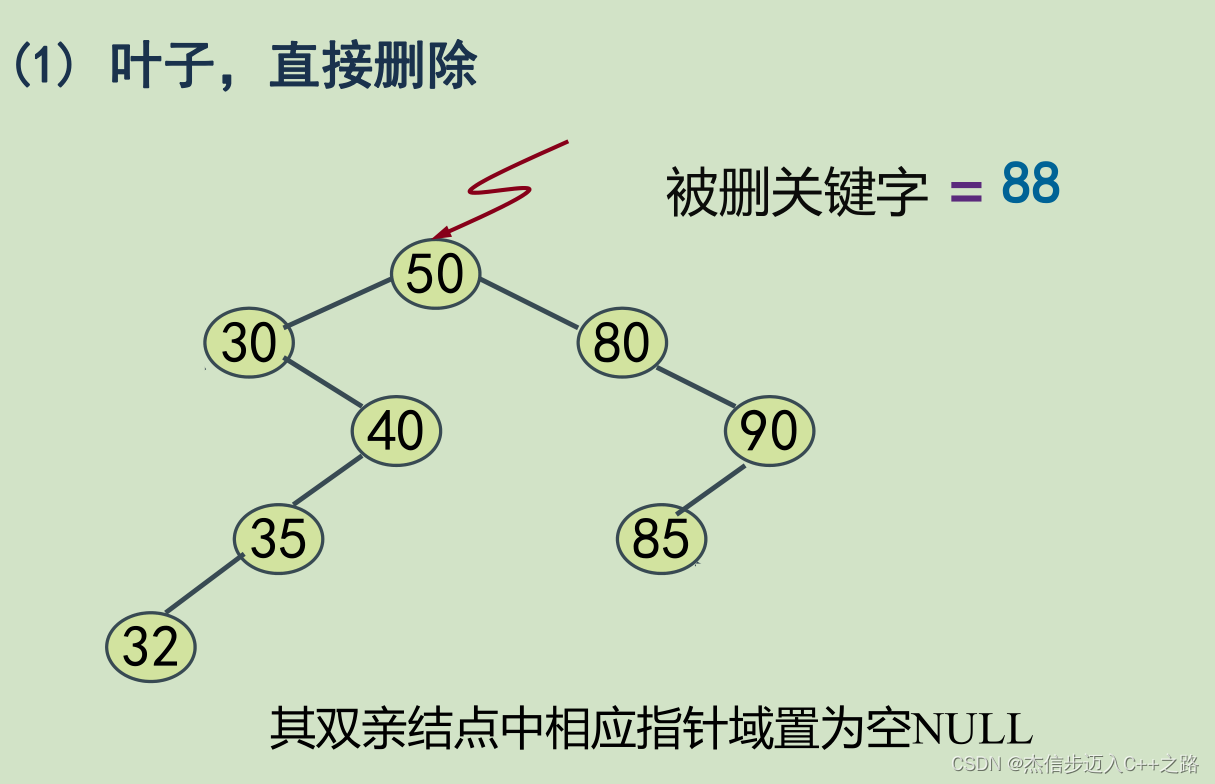
(1)被移除的结点是叶子结点
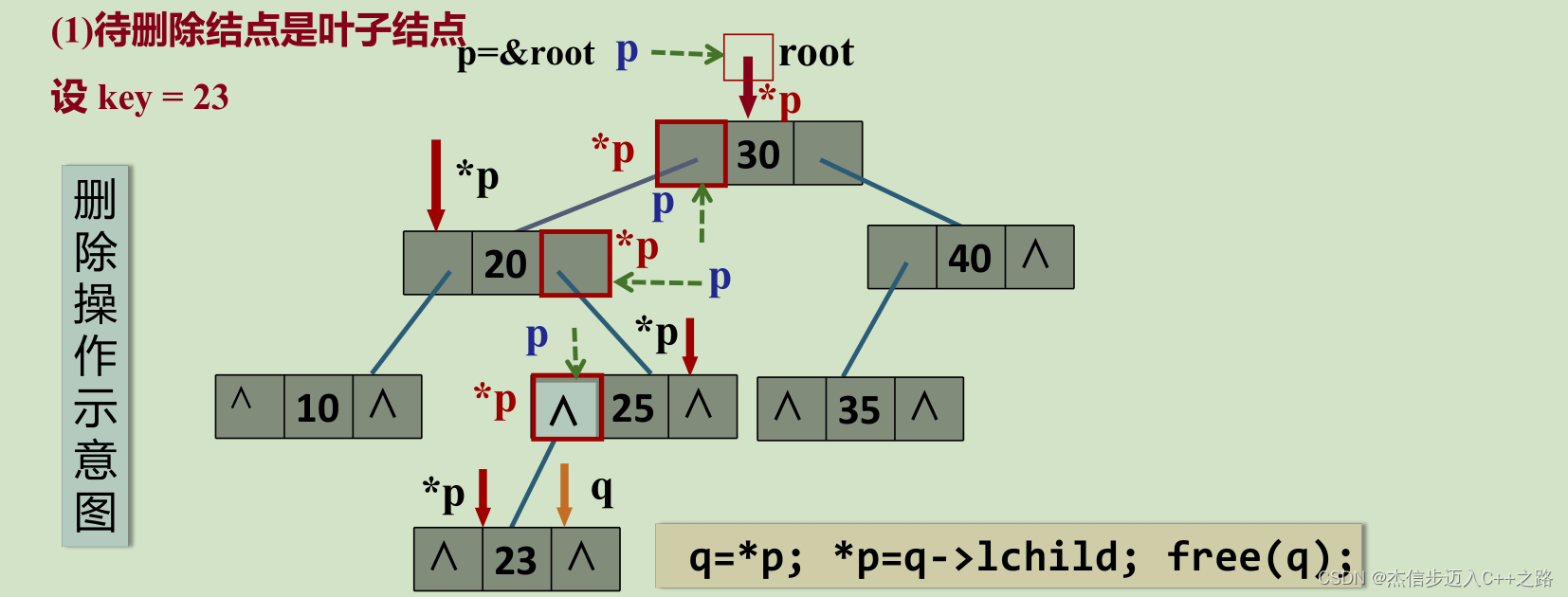
删除操作中的指针变量p在查找过程中存放的是结点左孩子变量或右孩子变量的地址,*p是结点的左孩子或右孩子变量。一旦查找成功,*p中存放的是待删结点的地址,*p指向待删除结点。q记被删除的结点,以便释放被删除结点的空间
(2)被移除的结点只有左子树或者只有右子树;
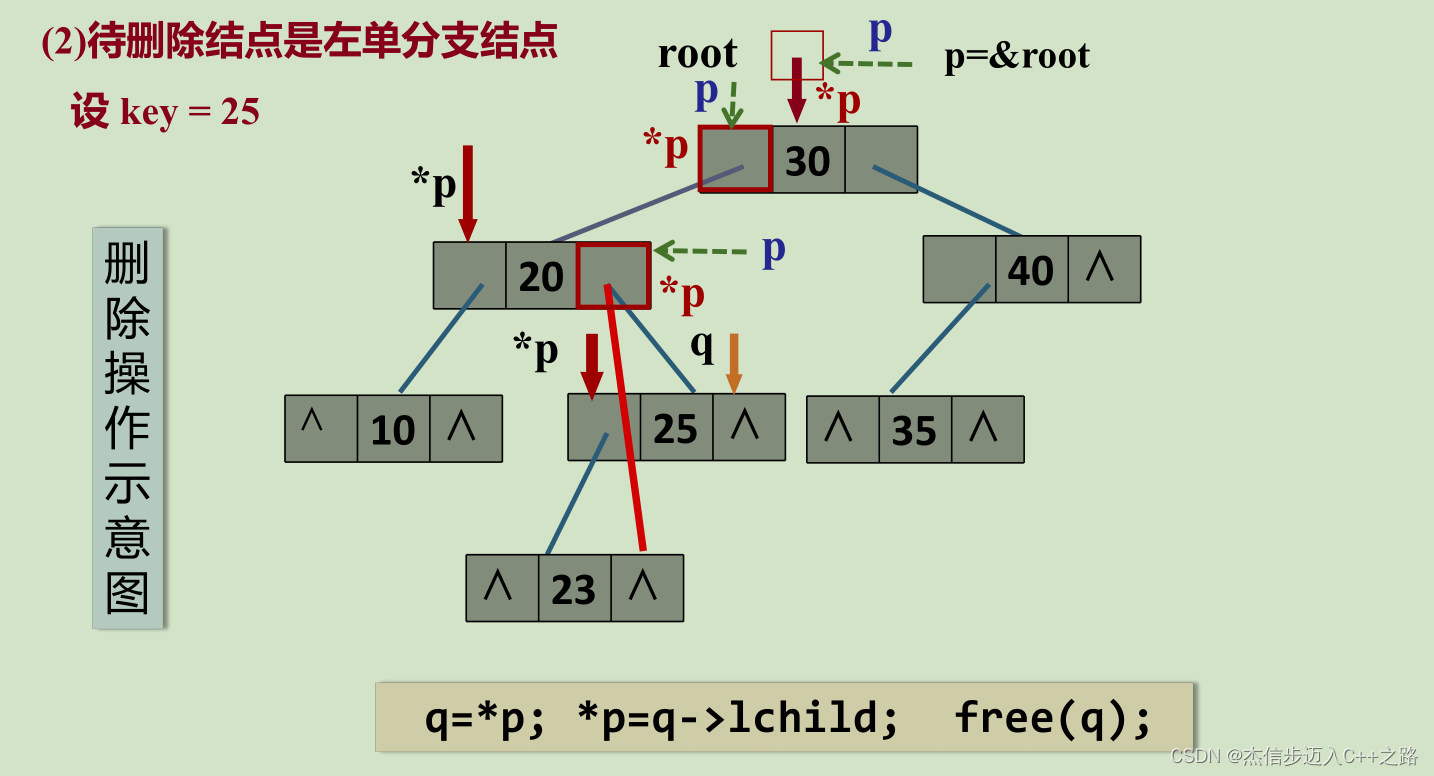
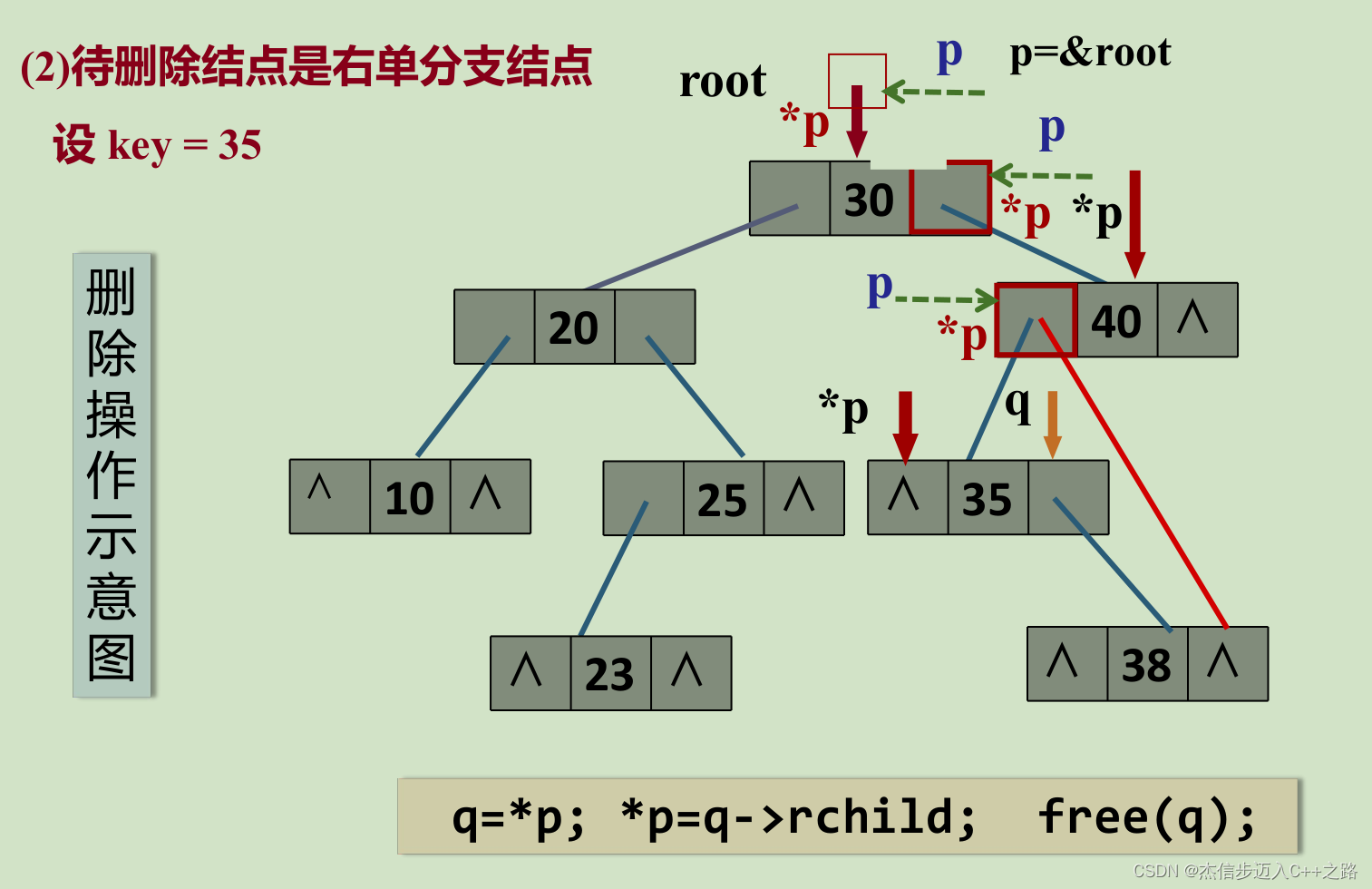
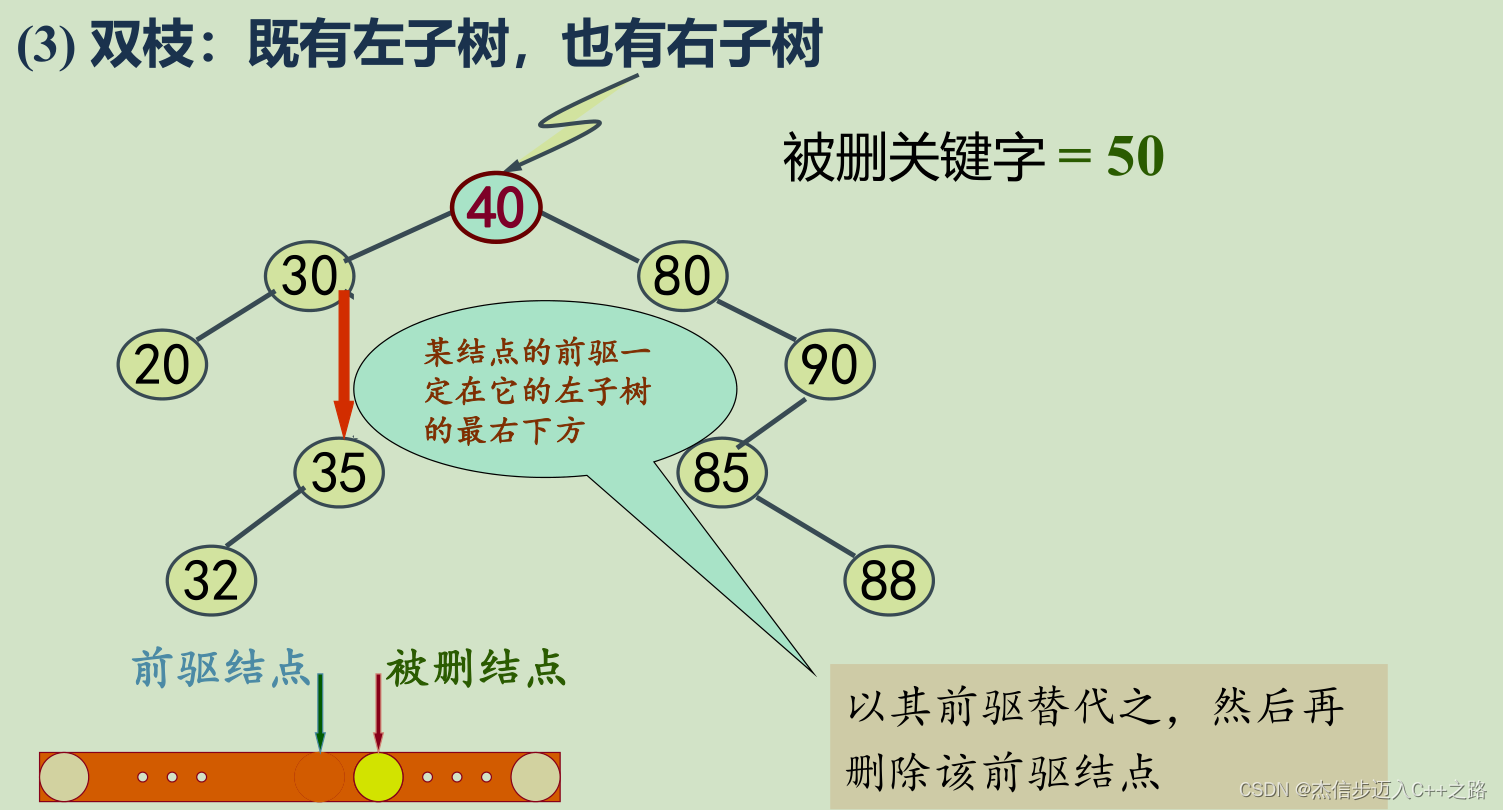
(3)被移除的结点既有左子树,也有右子树。
前驱替换方案:找到被删除结点的中序前驱(即左分支中的最大值),替换待删结点的值,并删除该前驱。
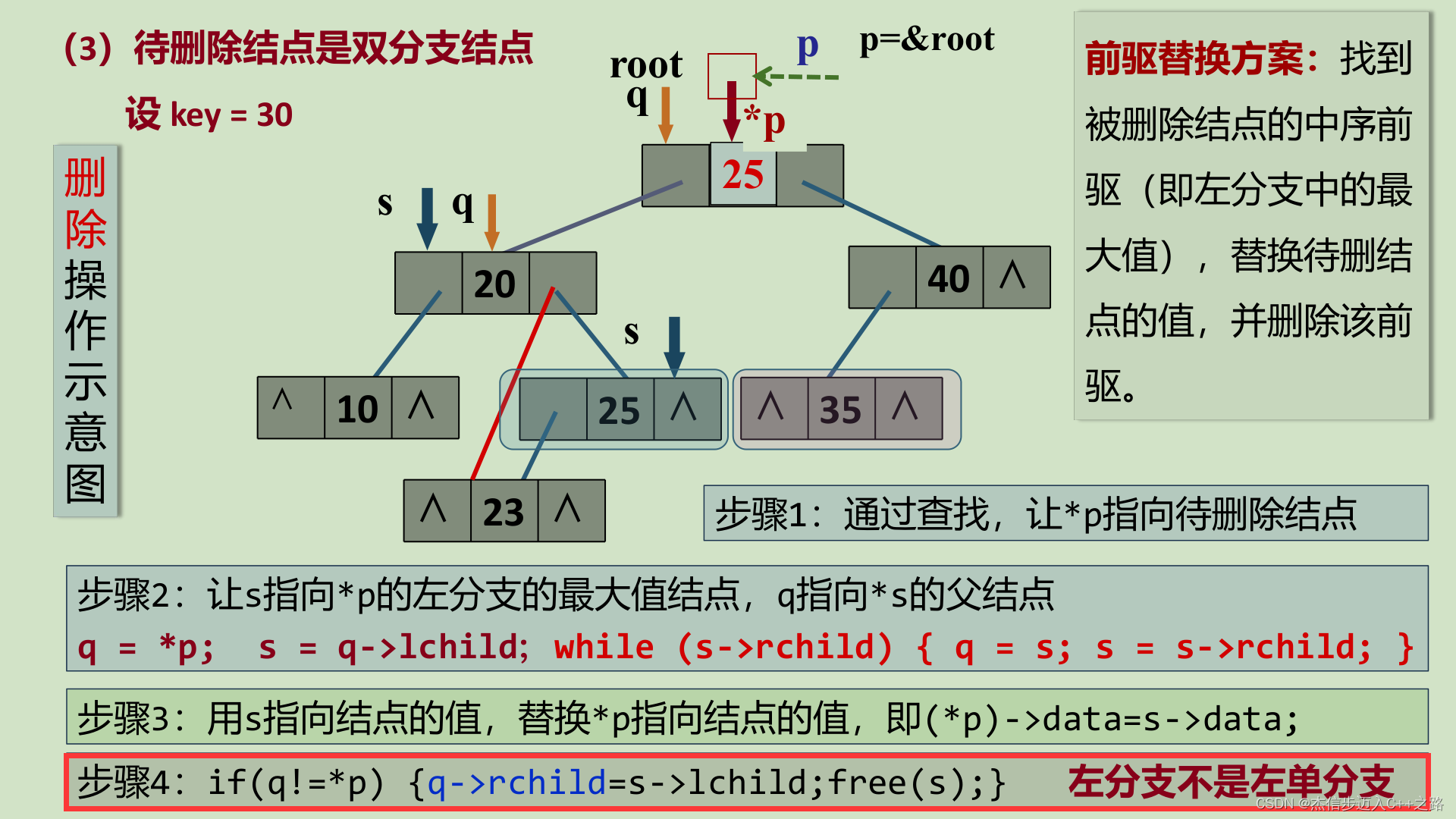
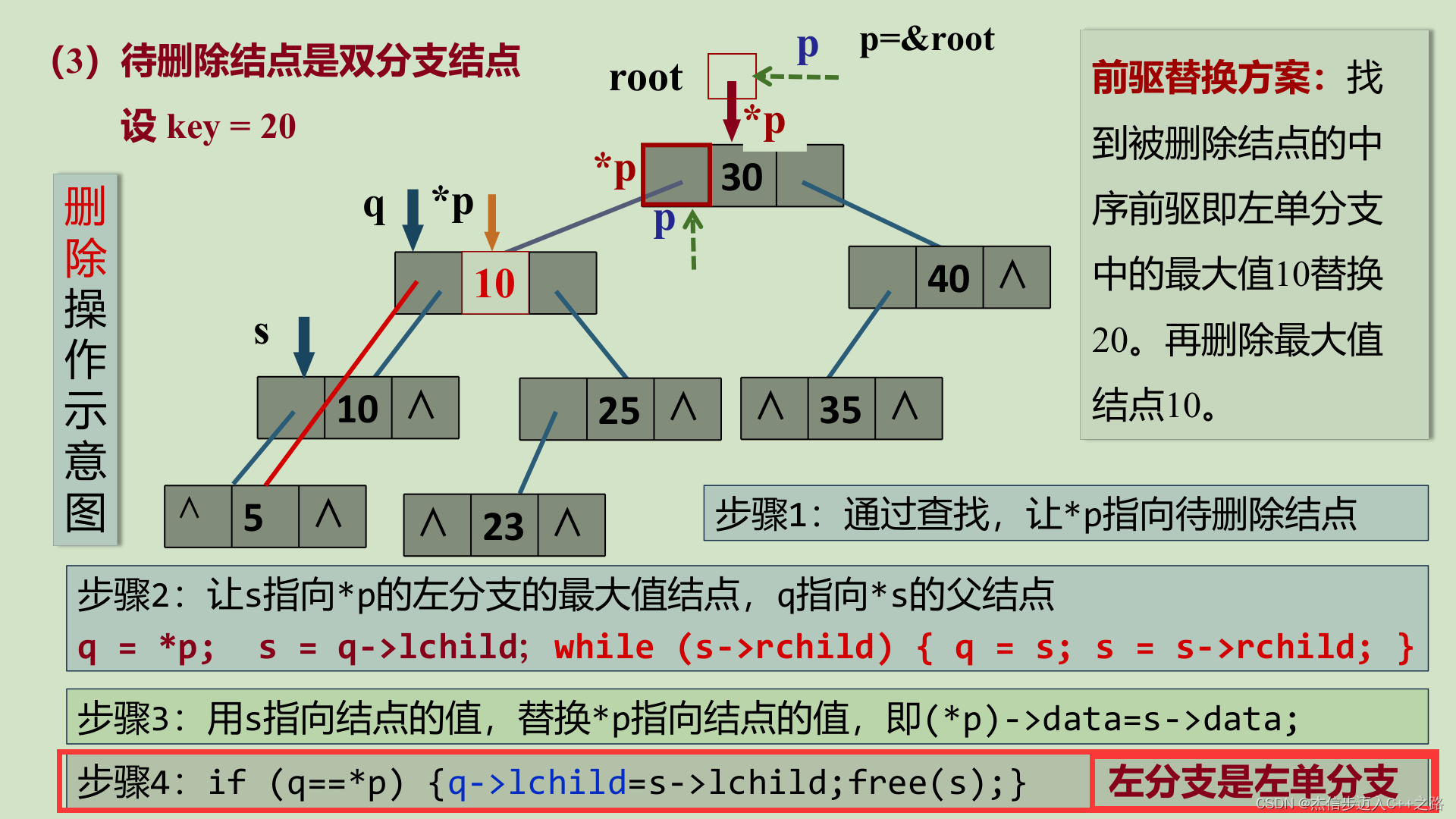
注意:左分支是否是左单分支
先找到在删除
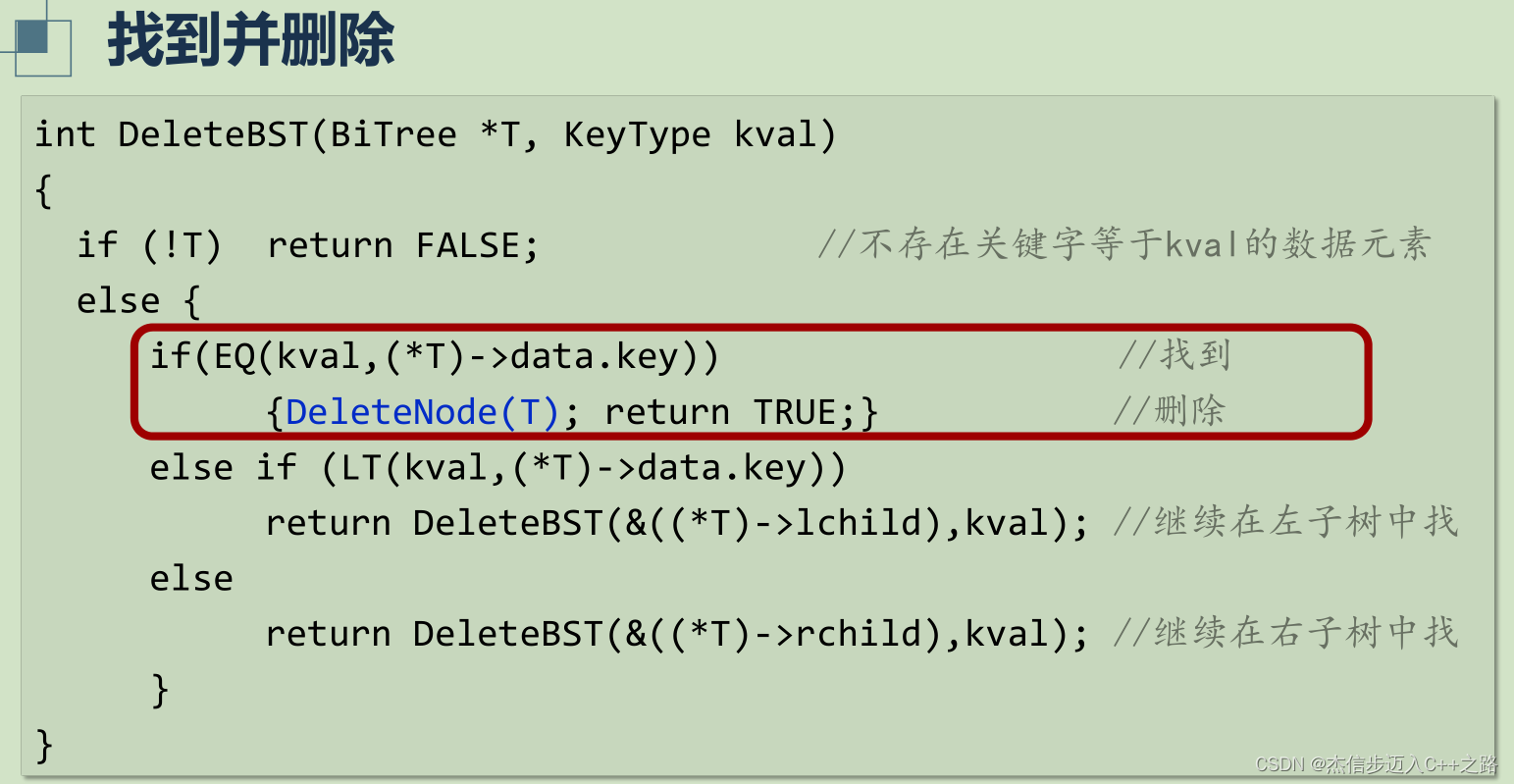
【删除描述】


1.6 性能分析
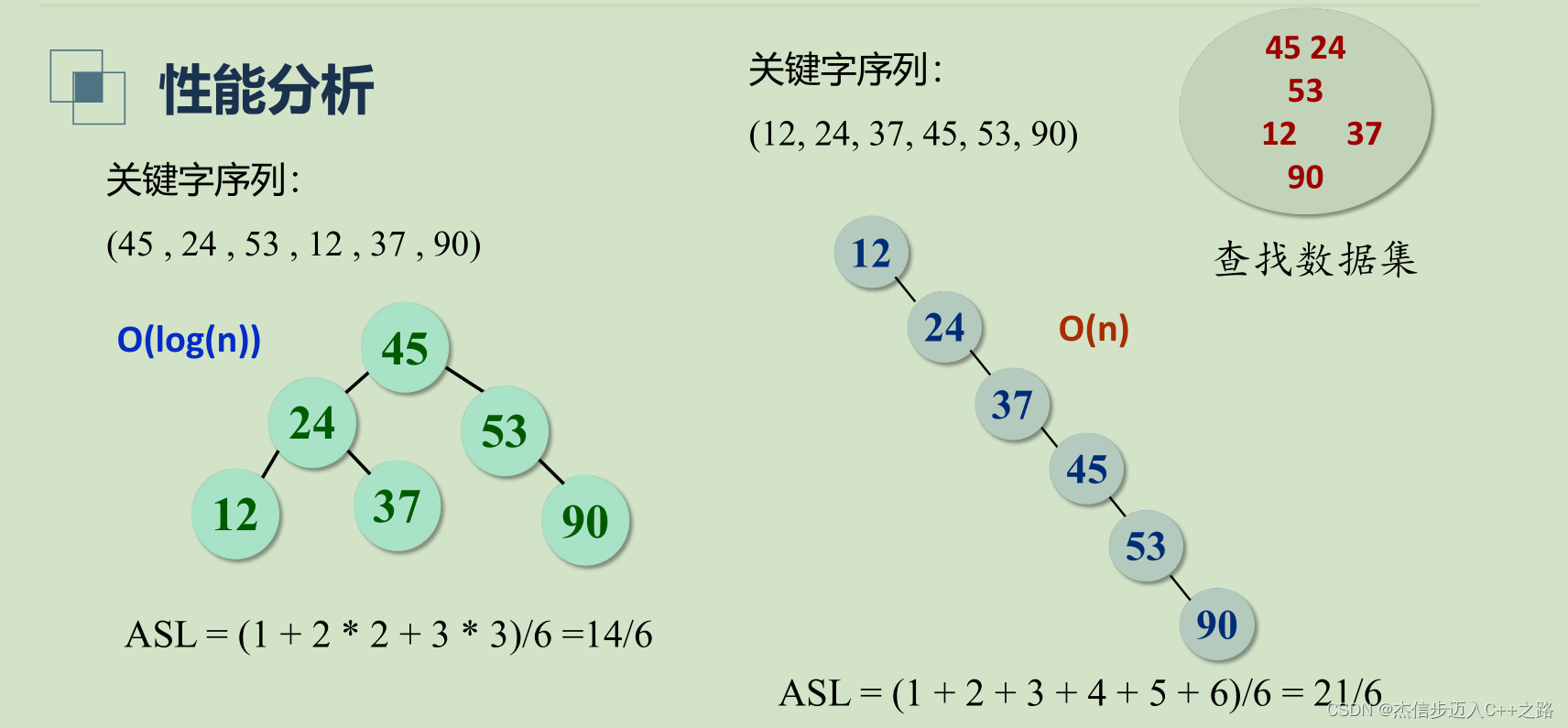
树的形状取决于关键字集合和插入次序
所以,为了保证二叉排序树的左右结点数均分,要在插入的时候进行调整,构建平衡二叉树
2.平衡二叉树

2.1 定义
什么样的二叉排序树是平衡二叉树?
结点的平衡因子:该结点的左子树的深度H L 与右子树的深度H R 之差
平衡二叉树:或者是一棵空的二叉排序树,或者是具有下列性质的二叉排序树:
- 根结点的左子树和右子树的平衡因子为-1、0或1;
- 根结点的左子树和右子树也都是二叉平衡树。
结点的平衡因子=左子树的深度H L - 右子树的深度H R
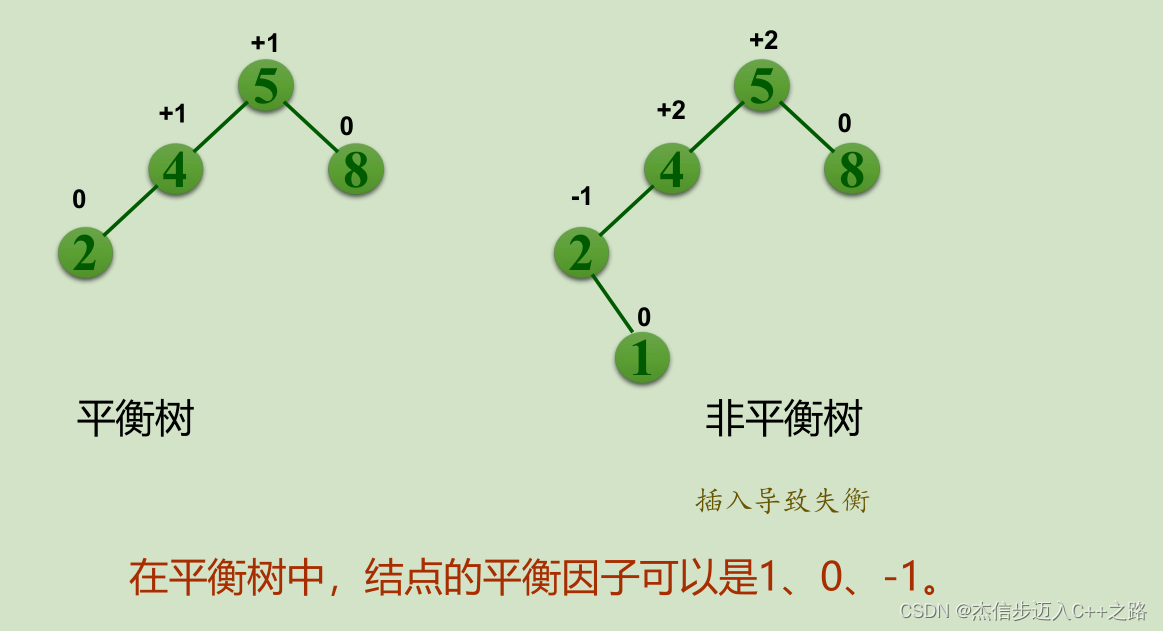
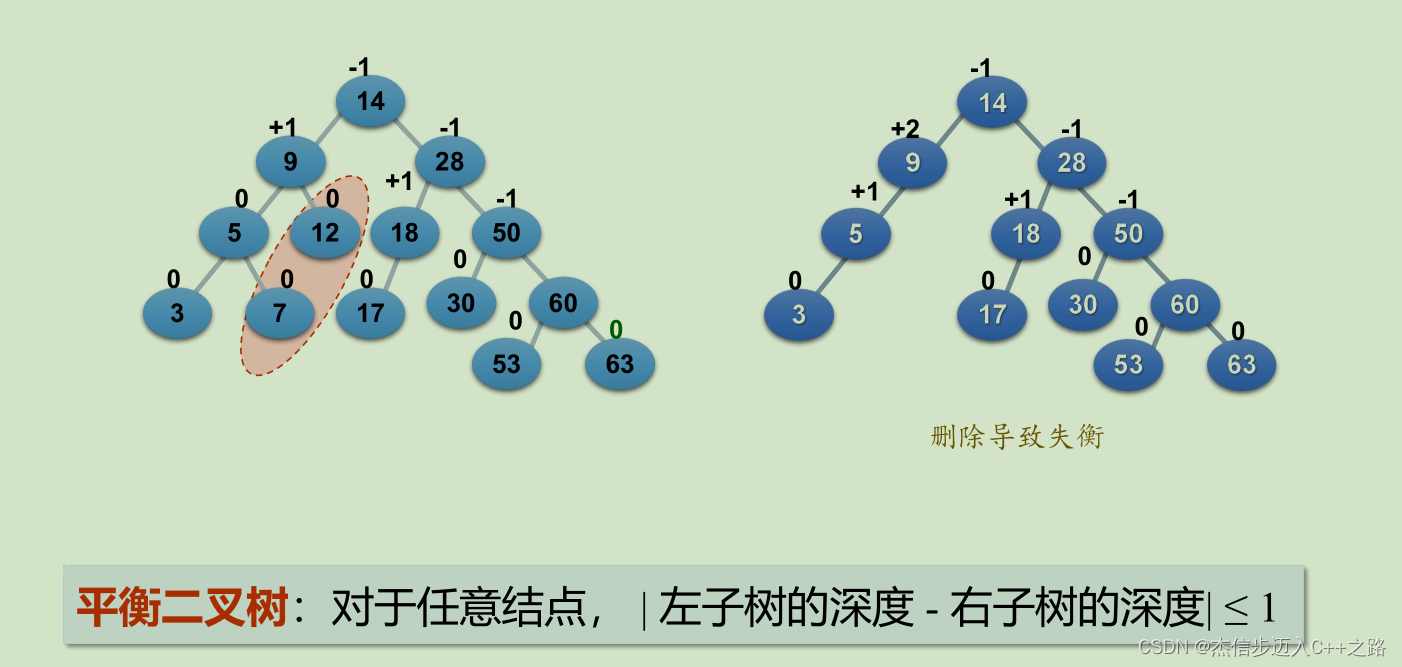
现象:一棵平衡二叉树,结点的插入或删除,都可能会导致失衡
最小不平衡子树:失衡的结点及其关联结点构成的是一棵高度为2的子树,由三个结点、两条边构成。
对策:针对这棵子树,做平衡化处理(Rebalance)
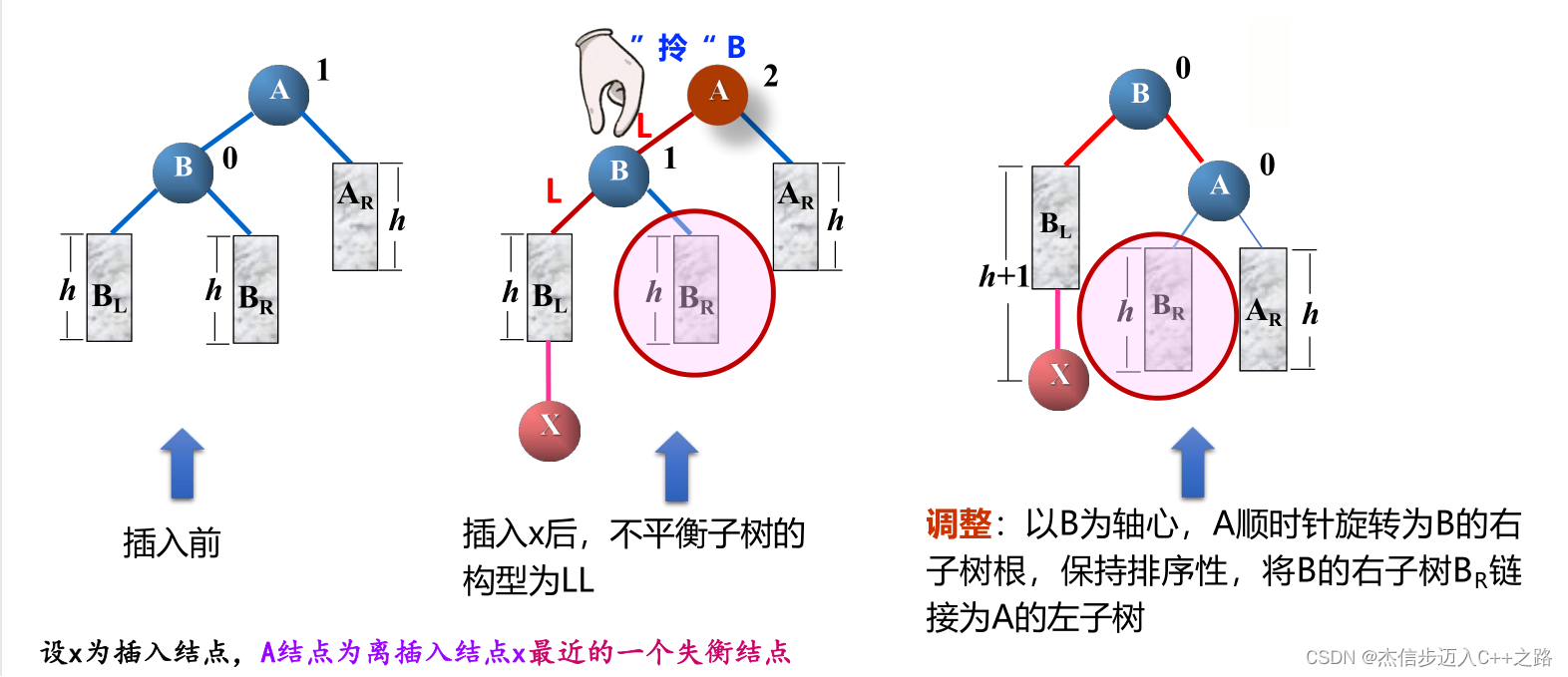
2.2. 插入时的最小不平衡子树
平衡因子的计算:每当插入一个新结点时,都需要重新计算从新插入的结点到根结点的
路径上所包含结点的平衡因子,一旦找到失衡点,停止计算。
最小不平衡子树:在根到插入结点的查找路径中,以距离插入结点最近的、且平衡因子
的绝对值大于1的结点为根,沿此查找路径再找两个结点构成这棵最小不平衡子树。
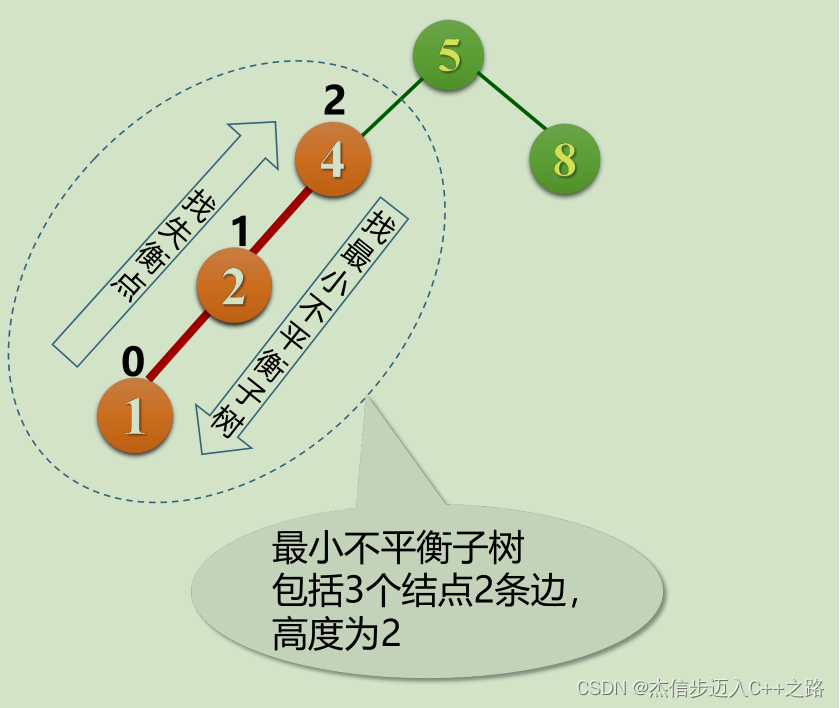
最小不平衡子树的调整再平衡(Rebalance)
在保持二叉排序树特性的前提下,调整最小不平衡子树中各结点之间的链接关系,进行相应的旋转,将最小不平衡子树的高度2降低到高度1,使之成为新的平衡子树
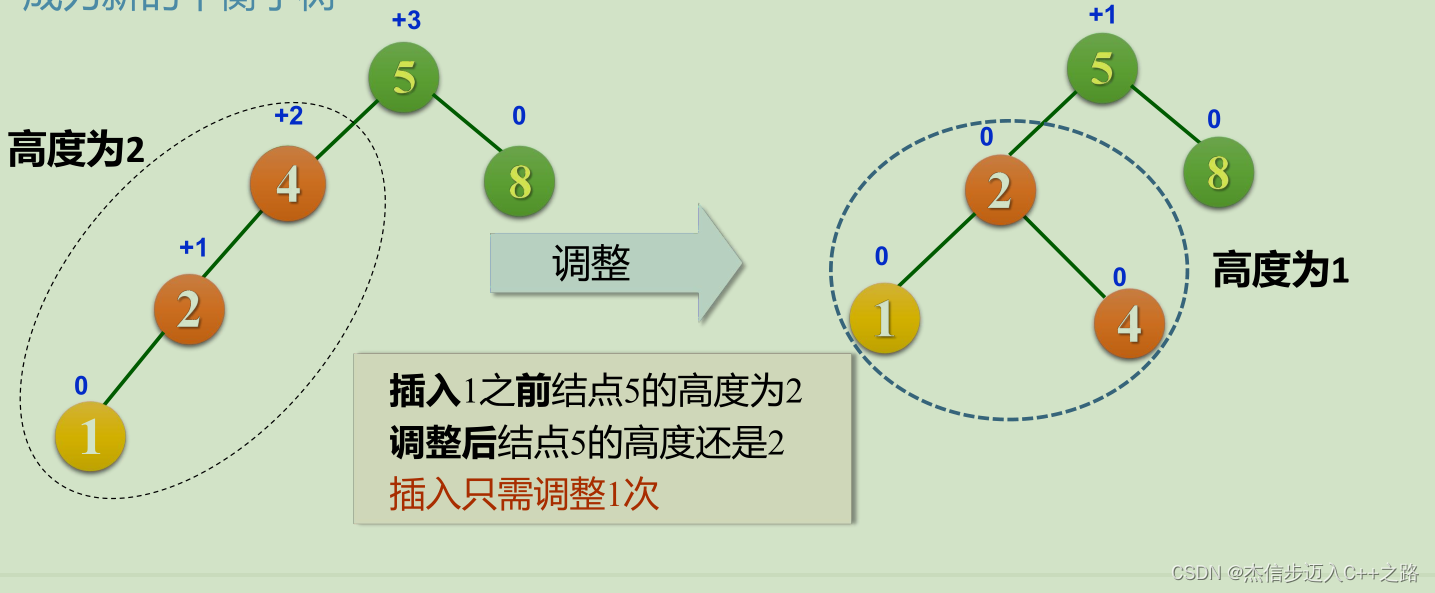
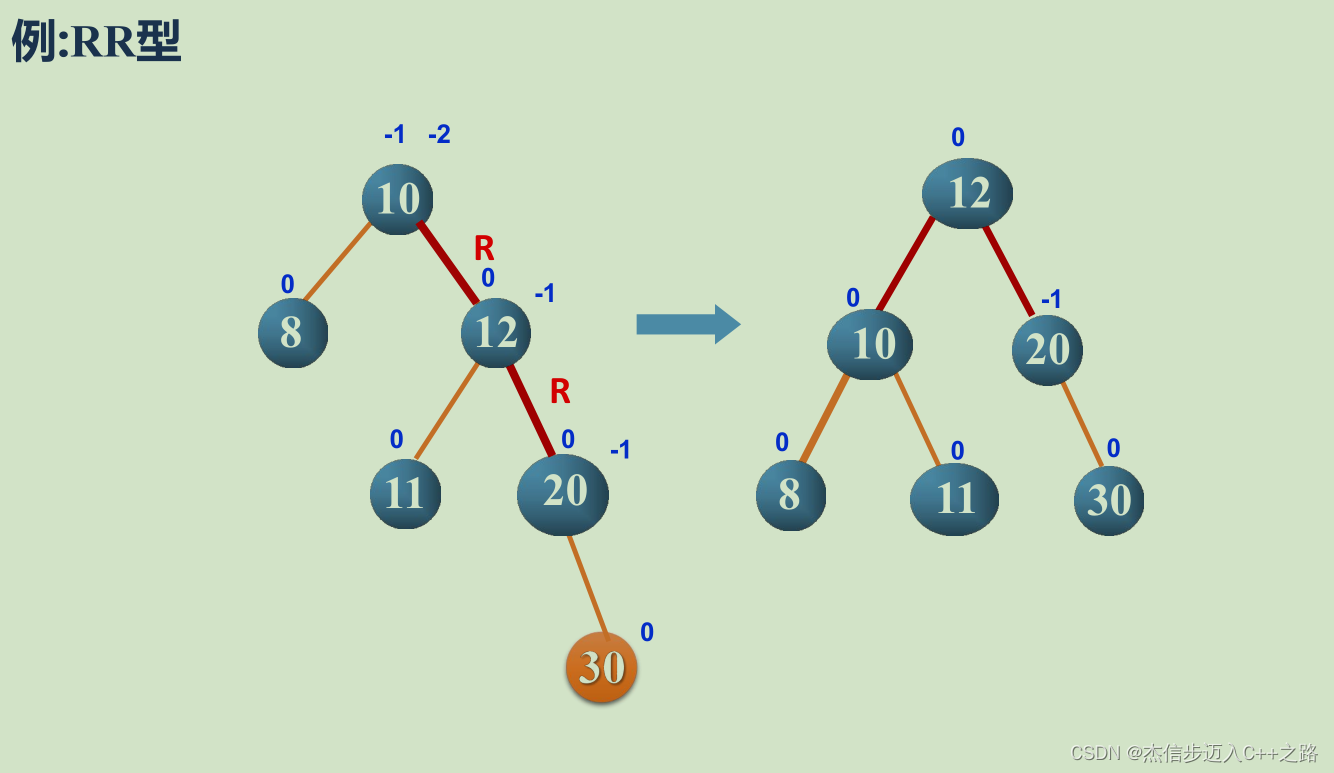
2.3. 最小不平衡子树调整类型
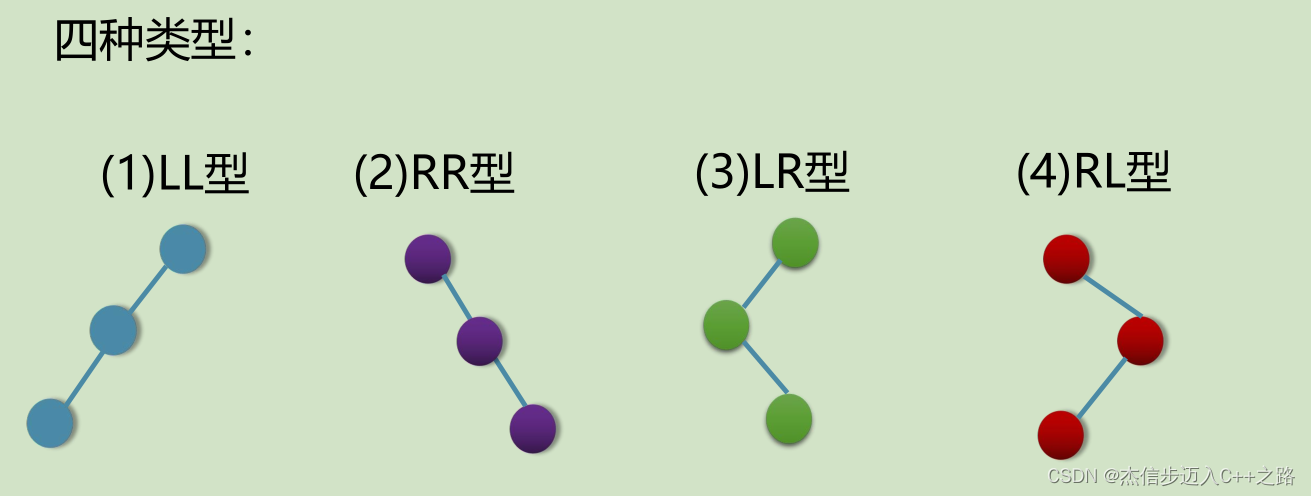
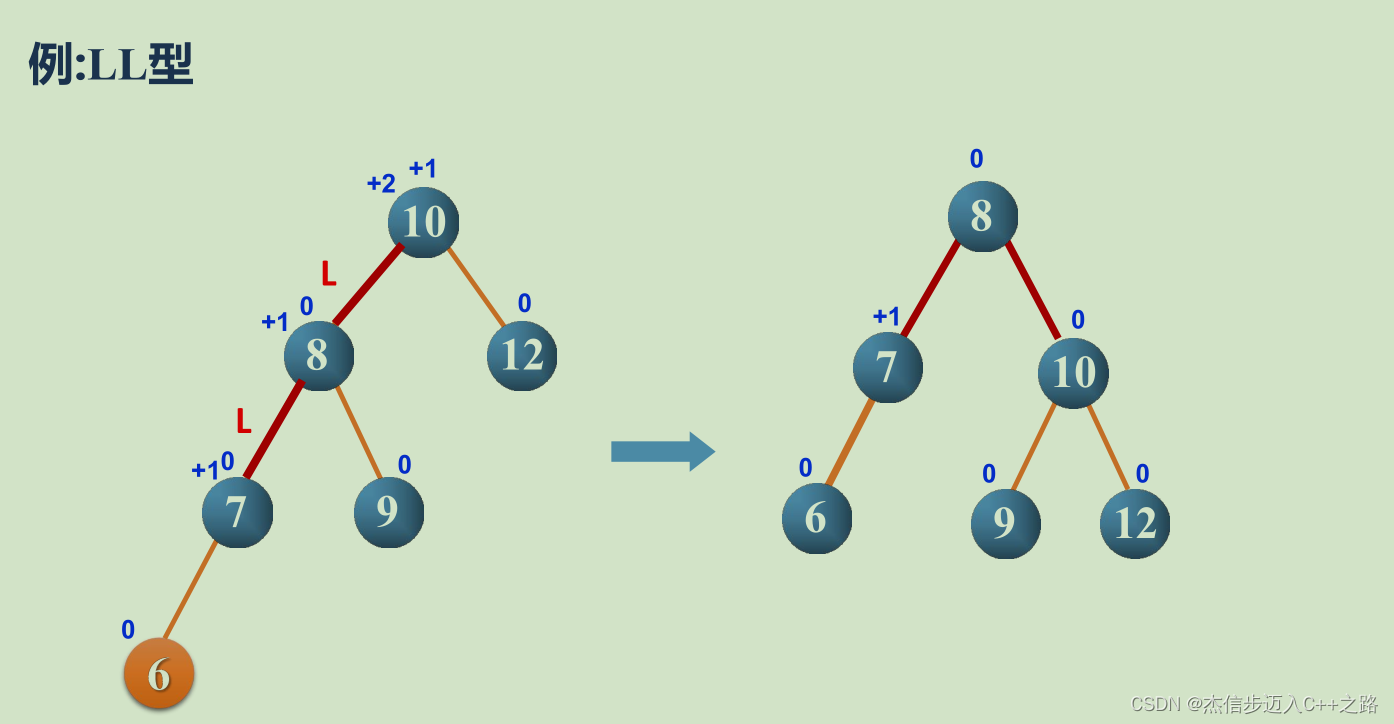
LL型
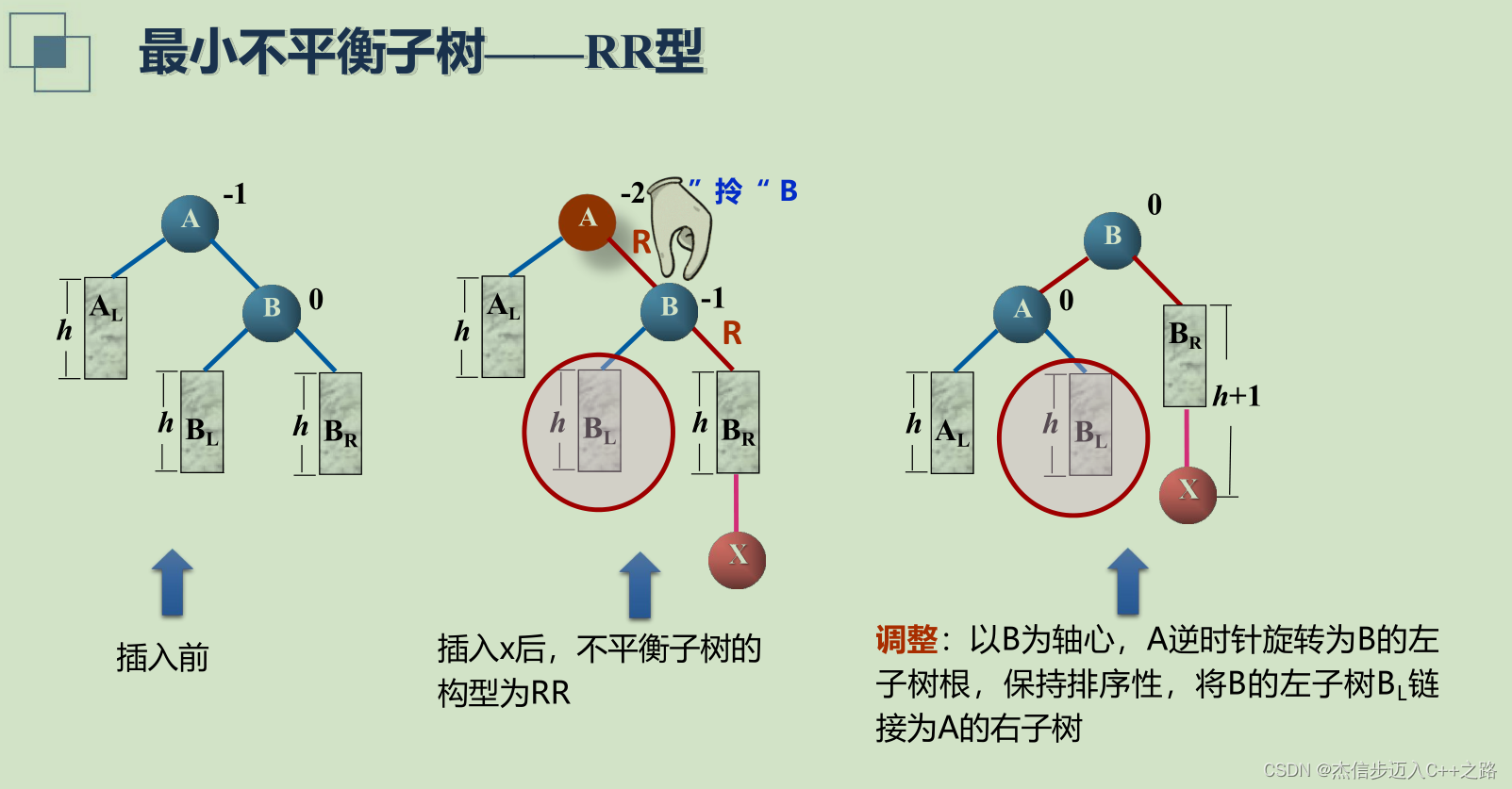
RR型
LR型
RL型
2.4 平衡二叉树的查找分析

2.5 平衡二叉树的结点删除

平衡二叉树删除结点后的处理
最小不平衡子树类型的确定
【例题】