EM算法实现对iris数据集和meat数据集的分类【MATLAB版本】

摘要：本章实验主要是对于学习 EM 算法的原理，掌握并实现混合高斯模型非监督学习的 EM 算法，要求在两个数据集上面实现混合高斯模型的非监督学习的ＥＭ算法。混合模型是相对于单高斯模型而言的，对于某个样本数据而言，可能单个高斯分布不能够很好的拟合其特征，而是由多个高斯模型混合加权而成（我们假设为Ｋ个），我们通过EM算法就可以求解出有未知参数情况的高斯模型的分布，进而完成无监督学习的分类任务。
关键字：混合高斯模型；EM算法；无监督学习。
Abstract: This chapter’s experiment aims to understand and implement the EM (Expectation Maximization) algorithm for unsupervised learning of the mixture Gaussian model. The EM algorithm is applied to two datasets to explore the application of the mixture Gaussian model in unsupervised learning. Compared to a single Gaussian model, the mixture model can better fit the features of sample data. The mixture model assumes that the sample data is a weighted combination of multiple Gaussian models (assumed to be K). The EM algorithm is used to estimate the Gaussian model distribution under unknown parameter conditions, thereby completing the classification task in unsupervised learning.
Keywords: Mixture Gaussian model, EM algorithm, unsupervised learning.

一、技术论述
(1) 所使用的主要知识是无监督学习的思想，最大似然估计方法，高斯混合模型假设以及ＥＭ算法。
（a）其中无监督学习是机器学习和模式识别的一个大类，机器学习主要分为有监督学习(带标签的学习）和无监督学习（无标签的学习），对于有标签的学习而言，我们主要是对其构造准则函数，然后根据不同的下降方法对其进行梯度下降（随机梯度下降，批量梯度下降等）寻优计算，最后找到对应的准则函数最小的那组权重就是我们所要得到的最优分类器的参数；而无监督学习是在没有数据标签的情况下，利用数据分布的特点构造分类器来完成对于样本的分类任务。
(b) 最大似然估计方法 (MLE) 是参数估计的一个重要方法，他主要利用的就是样本数据的分布特点，构造包含参数的最大似然函数，其理论认为最大似然函数的极值点所对应的参数值就我们想要求得的哪一组参数值，即“出现的事情就是最有可能发生事情”思想。
（c） EM算法，集期望最大化算法（Expectation Maximization, EM）它是最大似然的推广（MLE）其核心思想是根据已有的数据，递归估计似然函数的参数。EM算法在样本数据中某些特征丢失的情况下，仍然可以进行参数估计
在这里插入图片描述

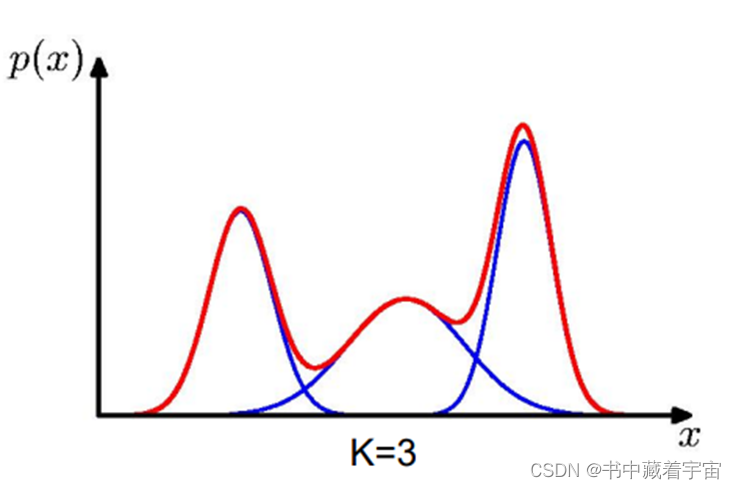图2-1：K=3的混合高斯模型

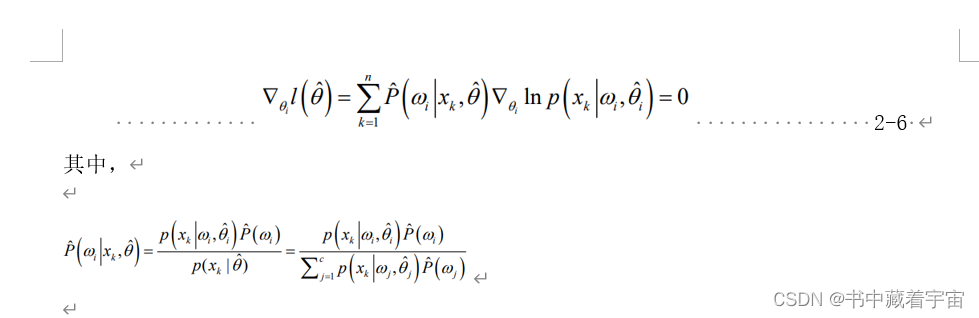
在这里插入图片描述

2.1 实验数据
(1)鸢尾花数据集
该数据集有150个样本，分为3类。每个样本有4个特征。
link
（2）UCI手写数字数据集“0-9”
数据集mfeat是由手写体数字“0”-“9”的特征数据集。1个手写数字有200个模式样本，总共有2000样本，存储在 ASCII 文本文件中，每1行存储一个样本的特征。其中，集合中的前200个样本是数字“0”的样本，后续200个样本分别是数字“1”-“9”的样本。
link
在这里插入图片描述

其中，
公式（1）中的π_k是针对某个k的q_nk的均值，是集合X中的所有样本属于第 k 类的后验概率之和；
公式（2）中的μ_k是以q_nk为权值的数据样本的均值（期望），是以后验概率为权值加权的均值（期望）
公式（3）中的Σ_k是以q_nk为权值的加权协方差矩阵，是以后验概率为权值加权的方差。
实验(一）
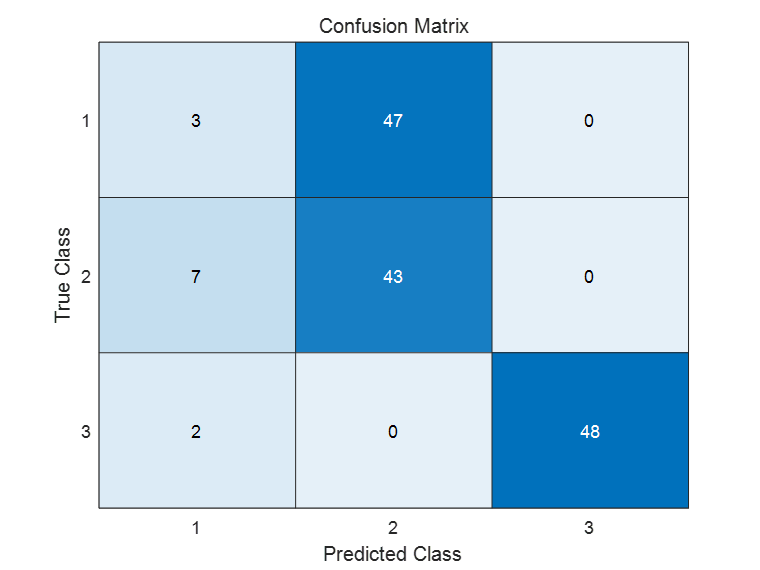
在这里插入图片描述
图3-1：混淆矩阵（迭代轮数为100）

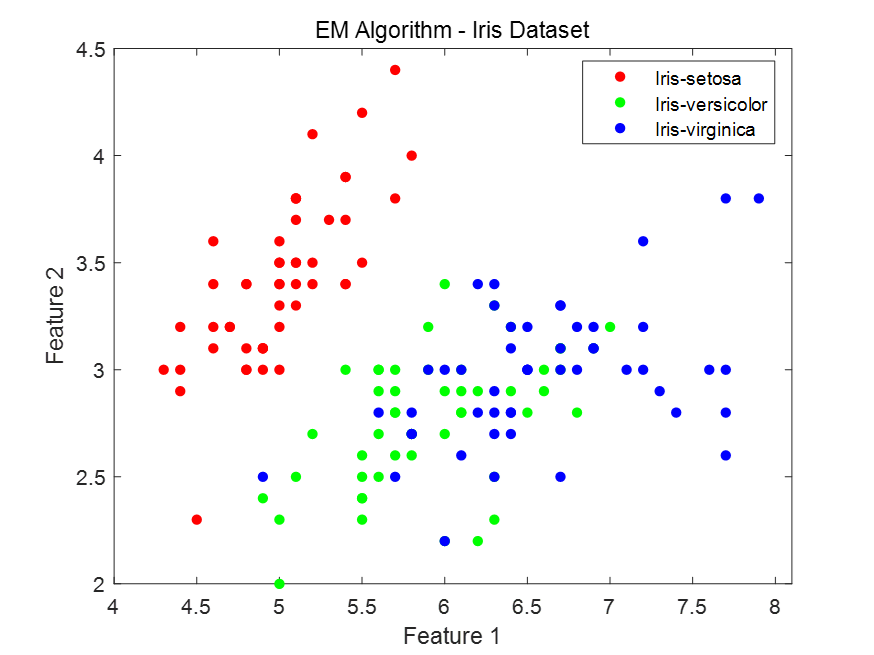
图3-2：取前两个特征的可视化结果（迭代轮数为100）

Total Accuracy: 0.62667
Class Accuracy:
0.0600
0.8600
0.9600
实验（二）：mfeat-fou数据集
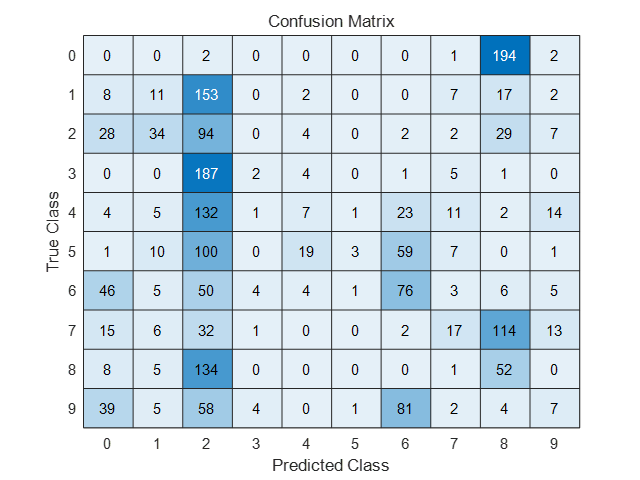
在这里插入图片描述
图3-3：混淆矩阵（迭代轮数为50）

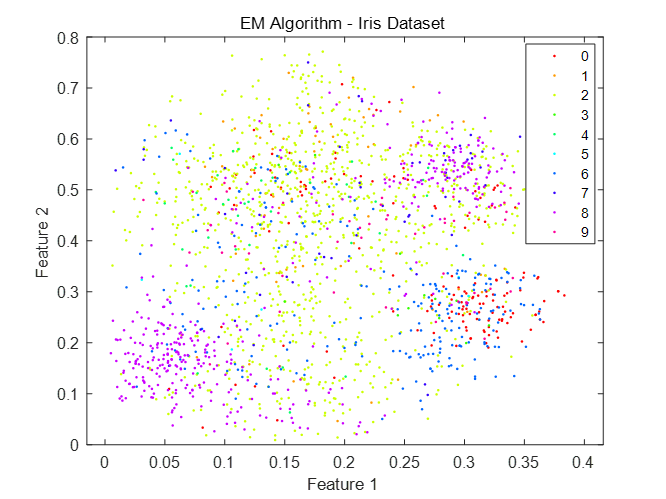
图3-4：取前两个特征的可视化结果（迭代轮数为5）
代码
实验一

clear all
clc
fid = fopen('iris.data', 'r');
data = textscan(fid, '%f,%f,%f,%f,%s');
fclose(fid);

% 提取特征数据，去除类别标签
features = cell2mat(data(:, 1:4));
% 将类别标签转换为数值标签
labels = data{:, 5}; % 获取类别标签数据
numericLabels = categorical(labels); % 转换为分类变量
% 初始化参数
numClusters = 3; % 分类簇的数量
maxIterations = 200; % 最大迭代次数

[numSamples, numFeatures] = size(features);
probabilities = zeros(numSamples, numClusters); % 各样本属于各分类的概率
means = repmat(min(features), numClusters, 1) + rand(numClusters, numFeatures) .* repmat(range(features), numClusters, 1);
covariances = repmat(diag(var(features)), 1, 1, numClusters); % 各分类的协方差矩阵

weights = ones(1, numClusters) / numClusters; % 各分类的权重

for iteration = 1:maxIterations
    % E 步骤：计算样本属于各分类的概率
    for i = 1:numClusters
        probabilities(:, i) = weights(i) * mvnpdf(features, means(i, :), squeeze(covariances(:, :, i)));
    end
    probabilities = probabilities ./ sum(probabilities, 2);
    
    % M 步骤：更新分类的均值、协方差矩阵和权重
    for i = 1:numClusters
        totalProb = sum(probabilities(:, i));
        weights(i) = totalProb / numSamples;
        means(i, :) = sum(probabilities(:, i) .* features) / totalProb;
        
        diff = features - means(i, :);
        covariances(:, :, i) = (diff' * (diff .* probabilities(:, i))) / totalProb;
    end
    
    % 计算分类准确率和混淆矩阵
    trueLabels = grp2idx(numericLabels);
    %对数据进行倒序
    trueLabels = flip( trueLabels);
    predictedLabels = zeros(numSamples, 1);

    for i = 1:numSamples
        [~, predictedLabels(i)] = max(probabilities(i, :));
    end

    totalAccuracy = sum(predictedLabels == trueLabels) / numSamples;
    classAccuracy = zeros(numClusters, 1);

    for i = 1:numClusters
        idx = trueLabels == i;
        classAccuracy(i) = sum(predictedLabels(idx) == trueLabels(idx)) / sum(idx);
    end


end
    disp(['Total Accuracy: ', num2str(totalAccuracy)]);
    disp('Class Accuracy:');
    disp(classAccuracy);
    
    % 绘制混淆矩阵
    confusionMatrix = confusionmat(trueLabels, predictedLabels);

    figure;
    heatmap(confusionMatrix, 'ColorbarVisible', 'off');
    xlabel('Predicted Class');
    ylabel('True Class');
    title('Confusion Matrix');
[~, labels] = max(probabilities, [], 2);

% 显示分类结果
figure;
gscatter(features(:, 1), features(:, 2), data{:, 5});
title('EM Algorithm - Iris Dataset');
xlabel('Feature 1');
ylabel('Feature 2');

实验二

clear all
clc
j=0;
load('-ascii','mfeat-kar.mat');
% 提取特征数据，去除类别标签
features = mfeat_kar;
trueLabels=zeros(2000,1);
% 将类别标签转换为数值标签
for i=1:1999
    trueLabels(i,1)=fix(i/200);
end
 trueLabels(2000,1)=9;
% 初始化参数
numClusters = 10; % 分类簇的数量
maxIterations = 50; % 最大迭代次数

[numSamples, numFeatures] = size(features);
probabilities = zeros(numSamples, numClusters); % 各样本属于各分类的概率
means = repmat(min(features), numClusters, 1) + rand(numClusters, numFeatures) .* repmat(range(features), numClusters, 1);
covariances = repmat(diag(var(features)), 1, 1, numClusters); % 各分类的协方差矩阵
weights = ones(1, numClusters) / numClusters; % 各分类的权重
%求出的协方差矩阵因为维数之间有相关的关系，所以求出来的协方差矩阵不是正定矩阵，我们需要对其进行处理
for iteration = 1:maxIterations
    % E 步骤：计算样本属于各分类的概率
    for i = 1:numClusters
        covariances(:, :, i) = covariances(:, :, i) + 1e-7 * eye(numFeatures);%添加扰动，反之其非正定，避免Mvpdf函数报错
        probabilities(:, i) = weights(i) * mvnpdf(features, means(i, :), squeeze(covariances(:, :, i)));
    end
    probabilities = probabilities ./ sum(probabilities, 2);
    
    % M 步骤：更新分类的均值、协方差矩阵和权重
    for i = 1:numClusters
        totalProb = sum(probabilities(:, i));
        weights(i) = totalProb / numSamples;
        means(i, :) = sum(probabilities(:, i) .* features) / totalProb;
        
        diff = features - means(i, :);
        covariances(:, :, i) = (diff' * (diff .* probabilities(:, i))) / totalProb;
    end
    
    % 计算分类准确率和混淆矩阵
    predictedLabels = zeros(numSamples, 1);

    for i = 1:numSamples
        [~, predictedLabels(i)] =max(probabilities(i, :));
    end
      for i = 1:numSamples
          predictedLabels(i)=predictedLabels(i)-1;
      end

    totalAccuracy = sum(predictedLabels == trueLabels) / numSamples;
    classAccuracy = zeros(numClusters, 1);

    for i = 1:numClusters
        idx = trueLabels == i;
        classAccuracy(i) = sum(predictedLabels(idx) == trueLabels(idx)) / sum(idx);
    end


end
    disp(['Total Accuracy: ', num2str(totalAccuracy)]);
    disp('Class Accuracy:');
    disp(classAccuracy);

    % 绘制混淆矩阵
    % 计算分类准确率和混淆矩阵
    labelsAdjusted = 0:numClusters-1; % 调整后的标签，从0开始
    confusionMatrix = confusionmat(trueLabels, predictedLabels);
    figure;
    heatmap(labelsAdjusted, labelsAdjusted,   confusionMatrix, 'ColorbarVisible', 'off');
    xlabel('Predicted Class');
    ylabel('True Class');
    title('Confusion Matrix');
[~, labels] = max(probabilities, [], 2);

% 显示分类结果
figure;
gscatter(features(:, 1), features(:, 2), labels-1);
title('EM Algorithm - Iris Dataset');
xlabel('Feature 1');
ylabel('Feature 2');