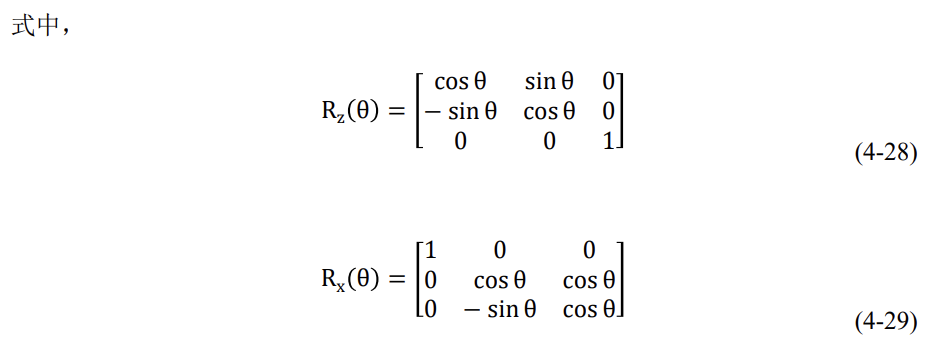📖 前言:线性回归(Lincar Regression)模型是最简单的线性模型之一,简而言之就像一元一次函数,是所有机器学习初学者的起点。而逻辑回归(Logistic Regression)则稍显复杂,是线性回归的一个推广,采用对数几率,他们都是其中最为经典的算法之一。最后引出分类评价指标,学会如何科学的评判一个模型的优劣。

目录
- 🕒 1. 什么是回归
- 🕒 2. 线性回归
- 🕘 2.1 概念
- 🕘 2.2 损失函数
- 🕘 2.3 其他评价指标
- 🕘 2.4 语法
- 🕘 2.5 步骤小结
- 🕒 3. 增加多项式特征
- 🕘 3.1 语法
- 🕒 4. 正则化
- 🕘 4.1 套索回归(L1)☆☆☆
- 🕤 4.1.1 效果
- 🕤 4.1.2 分析
- 🕤 4.1.3 语法
- 🕘 4.2 岭回归(L2)☆☆☆
- 🕤 4.2.1 效果
- 🕤 4.2.2 分析
- 🕤 4.2.3 语法
- 🕘 4.3 弹性网络回归(ElasticNet)
- 🕤 4.3.1 语法
- 🕒 5. 超参数调优
- 🕒 6. 综合案例:波士顿房价预测
- 🕒 7. 逻辑回归
- 🕘 7.1 概念
- 🕘 7.2 判定边界(决策边界)
- 🕤 7.2.1 一个特征两个标签
- 🕤 7.2.2 两个特征两个标签(二元分类)
- 🕤 7.2.3 两个特征三个标签(多分类)
- 🕘 7.3 损失函数
- 🕘 7.4 语法
- 🕒 8. 线性回归和逻辑回归的异同
- 🕒 9. 分类评价指标
- 🕘 9.1 精度指标的局限性
- 🕘 9.2 混淆矩阵☆☆☆
- 🕘 9.3 查准率与查全率、P-R曲线与F1分数☆☆☆
- 🕘 9.4 宏平均和微平均☆☆☆
- 🕘 9.5 ROC曲线和AUC
- 🕤 9.5.1 ROC曲线
- 🕤 9.5.2 绘制ROC曲线
- 🕤 9.5.3 ROC曲线的意义
- 🕤 9.5.4 AUC
- 🕘 9.6 语法
- 🕒 10. 综合案例:泰坦尼克号乘客生还预测
- 🕒 12. 课后习题
🕒 1. 什么是回归
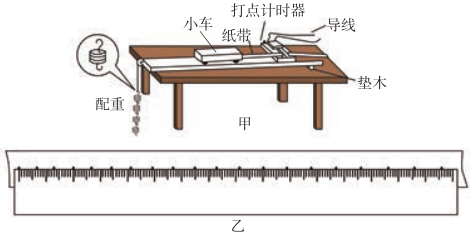
“回归”这个词看起来陌生,其实在高中物理实验中,大家经常借助回归思想,来寻求事物运动的特点和规律。其中一个经典的实验就是借助打点计时器和纸带,来探究小车速度随时间变化的规律。在实验过程中,同学们可以基于实验获取的数据来推断数据之间蕴含的关系。简单地说,“回归”就是一种由果索因的过程,即由大量事实所呈现的状态,设法去推断其形成的原因。
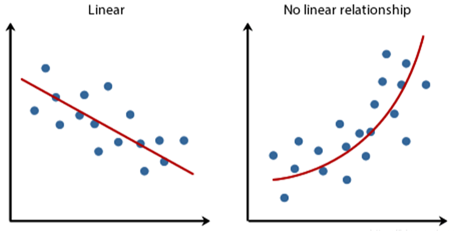
回归算法一般用于确定两种或两种以上变量间的定量关系。按照自变量的数量多少,可以分为一元回归和多元回归;按照自变量和因变量之间的关系类型,可以分为线性回归和非线性回归。因变量和自变量之间的关系如果类似于一次函数、则属于线性(Linear)回归问题;如果类似于指数函数或对数函数等,则属于非线性(No Linear)回归问题。
回归分析一般适用于求解因变量是连续值的情况,而不适用于求解因变量是离散值的情况。如明天的气温、超市每天的销售额、近期的房屋价格和股票走势等适合用回归分析法求解,而明天是否下雨、图片中的动物是小猫还是小狗等则属于分类问题(如K近邻、逻辑回归)。
🕒 2. 线性回归
🕘 2.1 概念
在电影票房的预测中,我们可以使用线性回归预测
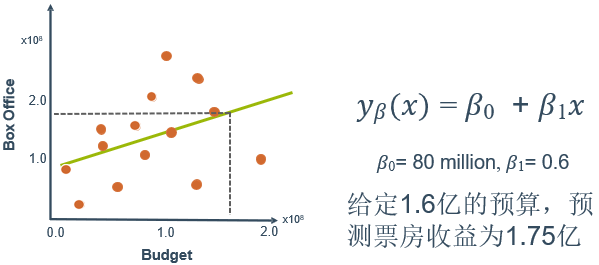
上面的一元线性模型只考虑了对票房产生影响的一个特征——电影票价。如果考虑对票房产生影响的多个特征,即剧情水平、观影效果、口碑、宣传等,就会构成一个含有多个变量的模型,模型中的特征记为
(
x
1
,
x
2
,
.
.
.
,
x
n
′
)
(x_1,x_2,...,x_n ')
(x1,x2,...,xn′)即可得到多元线性回归模型:
y
β
(
x
1
,
x
2
,
⋯
,
x
n
)
=
β
0
+
β
1
x
1
+
⋯
+
β
n
x
n
y_{\beta}\left(x_{1}, x_{2}, \cdots, x_{n}\right)=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{n} x_{n}
yβ(x1,x2,⋯,xn)=β0+β1x1+⋯+βnxn
🕘 2.2 损失函数
损失函数在每一种机器学习算法中都很重要,因为训练模型的过程就是最小化损失函数的过程。
我们以一元线性回归模型为例,多元线性回归与其类似。
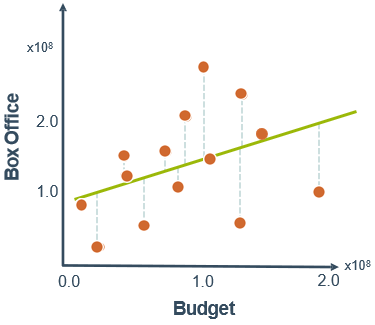
还是电影票房的例子,选择不同的参数值,会得到不同的函数。选择的参数值决定了所得到的直线相对于训练集的准确程度,即预测值与真实(测量)值之间的差异就是残差(下图中的虚线),也就是建模误差(modeling error),记为:
y
β
(
x
o
b
s
(
i
)
)
−
y
o
b
s
(
i
)
y_{\beta}\left(x_{o b s}^{(i)}\right)-y_{o b s}^{(i)}
yβ(xobs(i))−yobs(i) ,把x代入y即
(
β
0
+
β
1
x
o
b
s
(
i
)
)
−
y
o
b
s
(
i
)
\left(\beta_{0}+\beta_{1} x_{o b s}^{(i)}\right)-y_{o b s}^{(i)}
(β0+β1xobs(i))−yobs(i)。我们的目标便是找到使平均建模误差(平方)最小的模型参数,即
1
m
∑
i
=
1
m
(
(
β
0
+
β
1
x
o
b
s
(
i
)
)
−
y
o
b
s
(
i
)
)
2
\frac{1}{m} \sum_{i=1}^{m}\left(\left(\beta_{0}+\beta_{1} x_{o b s}^{(i)}\right)-y_{o b s}^{(i)}\right)^{2}
m1i=1∑m((β0+β1xobs(i))−yobs(i))2
这就是均方误差(Mean Squared Error, MSE)
最小均方误差为:
min
β
0
,
β
1
1
m
∑
i
=
1
m
(
(
β
0
+
β
1
x
o
b
s
(
i
)
)
−
y
o
b
s
(
i
)
)
2
\min _{\beta_{0}, \beta_{1}} \frac{1}{m} \sum_{i=1}^{m}\left(\left(\beta_{0}+\beta_{1} x_{o b s}^{(i)}\right)-y_{o b s}^{(i)}\right)^{2}
β0,β1minm1i=1∑m((β0+β1xobs(i))−yobs(i))2
其中 min β 0 , β 1 \min _{\beta_{0}, \beta_{1}} minβ0,β1的意思是通过调节参数 β 0 \beta_{0} β0和 β 1 \beta_{1} β1来达到求最小值。
β 0 \beta_{0} β0的调节方法: β 0 新 = β 0 旧 − 学 习 率 × 损 失 值 \beta_{0}新 = \beta_{0}旧 - 学习率 \times 损失值 β0新=β0旧−学习率×损失值
通过梯度下降(最小二乘法的一种更简单的方法)等优化方法求得最小值时,
损失值通过损失函数对 β 0 \beta_{0} β0求偏导计算求得,这个偏导也称为梯度,通过损失值来调节 β 0 \beta_{0} β0,不断缩小损失值直到最小,这也正是梯度下降的得名来由。当然这个被求偏导的函数必须是个凸函数,即连续可导。
学习率是一个由外部输入的参数,被称为“超参数”,可以形象地理解为 β 0 \beta_{0} β0通过这一次错误学到多少,想要 β 0 \beta_{0} β0多调整一点,就把学习率调高一点。不过学习率也不是越高越好,过高的学习率可能导致调整幅度过大,错过了最佳收敛点,也就导致无法求得真正的最小值。这个在下面会提到。
有兴趣的同学可以参考这篇文章:🔎 最小二乘法和梯度下降法有哪些区别?
从而得出损失函数(代价函数):
J
(
β
0
,
β
1
)
=
1
2
m
∑
i
=
1
m
(
(
β
0
+
β
1
x
o
b
s
(
i
)
)
−
y
o
b
s
(
i
)
)
2
J\left(\beta_{0}, \beta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\left(\beta_{0}+\beta_{1} x_{o b s}^{(i)}\right)-y_{o b s}^{(i)}\right)^{2}
J(β0,β1)=2m1i=1∑m((β0+β1xobs(i))−yobs(i))2
前面乘上
1
2
\frac{1}{2}
21是为了在对损失函数求导数时消除误差平方项的影响。均方误差是解决回归问题最常用的损失函数。
求解:
1:J(belta)对belta偏导为0,可整理得方程组: x ‘ x b e l t a = x ‘ y x`x \ belta=x`y x‘x belta=x‘y,求解即可得belta解析解。
2:也可用梯度下降法求最优解。
🕘 2.3 其他评价指标
平均绝对误差(Mean Absolute Error, MAE):
1
m
∑
i
=
1
m
∣
y
β
(
x
(
i
)
)
−
y
o
b
s
(
i
)
∣
\frac{1}{m} \sum_{i=1}^{m}\left|y_{\beta}\left(x^{(i)}\right)-y_{o b s}^{(i)}\right|
m1i=1∑m∣∣∣yβ(x(i))−yobs(i)∣∣∣
均方根误差(Root Mean Squared Error, RMSE):
1
m
∑
i
=
1
m
(
y
β
(
x
(
i
)
)
−
y
o
b
s
(
i
)
)
2
\sqrt{\frac{1}{m} \sum_{i=1}^{m}\left(y_{\beta}\left(x^{(i)}\right)-y_{o b s}^{(i)}\right)^{2}}
m1i=1∑m(yβ(x(i))−yobs(i))2
残差平方和(SSE):
∑
i
=
1
m
(
y
β
(
x
(
i
)
)
−
y
o
b
s
(
i
)
)
2
\sum_{i=1}^{m}\left(y_{\beta}\left(x^{(i)}\right)-y_{o b s}^{(i)}\right)^{2}
i=1∑m(yβ(x(i))−yobs(i))2
总离差平方和(TSS):
∑
i
=
1
m
(
y
o
b
s
‾
−
y
o
b
s
(
i
)
)
2
\sum_{i=1}^{m}\left(\overline{y_{o b s}} {}-y_{o b s}^{(i)}\right)^{2}
i=1∑m(yobs−yobs(i))2
决定系数(R2):
1
−
S
S
E
T
S
S
1-\frac{S S E}{T S S}
1−TSSSSE
🕘 2.4 语法
导入包含回归方法的类:
from sklearn.linear_model import LinearRegression
创建该类的一个对象:
LR = LinearRegression()
训练模型拟合数据,并预测:
LR = LR.fit(X_train, y_train)
y_predict = LR.predict(X_test)
在线文档:🔎 回归方法的语法
LinearRegression():线性回归模型,优化算法为解析法,适用于小数据集;
其他优化算法的线性回归模型:如SDGRegression()(随机梯度下降,适用于大数据集:>10000,可设置max_iter和learning_rate等参数)
LinearRegression()参数:
fit_intercept:是否计算该模型的截距,默认True
normalize:是否对数据进行标准化处理,默认False
返回值的属性:
coef_:feature的系数
intercept_:截距
LinearRegression其他方法:
score(self, X, y[, sample_weight]):模型评估,返回R2系数,最优值为1,说明所有数据都预测正确
🕘 2.5 步骤小结
- 为假设函数设定参数w,通过假设函数画出一条直线,即根据输入的点通过线性计算得到预测值。
- 将预测值带入损失函数,计算出一个损失值。
- 通过得到的损失值,利用梯度下降等凸优化方法,不断调整假设函数的参数 β 0 \beta_{0} β0,使得损失值最小。这个不断调整参数 β 0 \beta_{0} β0使得损失值最小化的过程就是线性回归的学习过程,通常称为训练模型。
🕒 3. 增加多项式特征
线性回归模型是最简单的模型,有不少前提假设,其中最主要的一条就是不同特征之间存在线性关系。然而现实中的数据往往线性关系比较弱,甚至不存在线性关系。可以通过增加多项式特征,将线性关系扩展至非线性关系来进行广义的线性回归。
增加多项式特征就是把一次特征转换成高次特征的线性组合多项式,举例
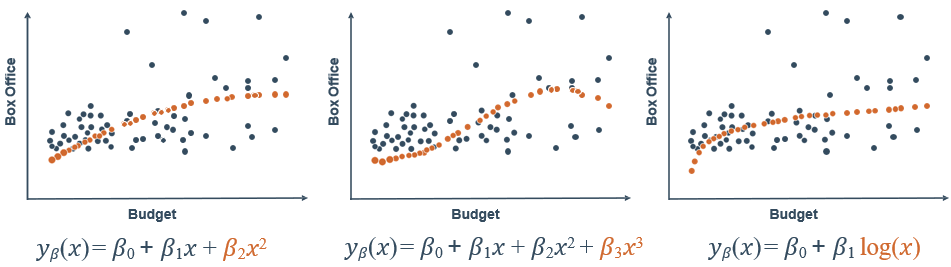
注意,这个最高次n应取合适的值,如果太大,模型会很复杂,容易过拟合。
-
可以选择变量间的交互项: y β ( x ) = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 1 x 2 y_{\beta}(x)=\beta_{0}+\beta_{1} x_1+\beta_{2} x_2+\color{brown}\beta_{3} x_1x_2 yβ(x)=β0+β1x1+β2x2+β3x1x2
-
如何选择正确的函数形式:→ 检查每个变量与结果之间的关系
❗ 转载请注明出处
作者:HinsCoder
博客链接:🔎 作者博客主页
🕘 3.1 语法
导入包含转换方法的类:
from sklearn.preprocessing import PolynomialFeatures
创建该类的一个对象:
polyFeat = PolynomialFeatures(degree=2) # 二次多项式
创建多项式特征,并转换数据:
polyFeat = polyFeat.fit(X_data)
x_poly = polyFeat.transform(X_data)
# 或者
x_poly = polyFeat.fit_transform(X_data)
在线文档:🔎 多项式特征的语法
🕒 4. 正则化
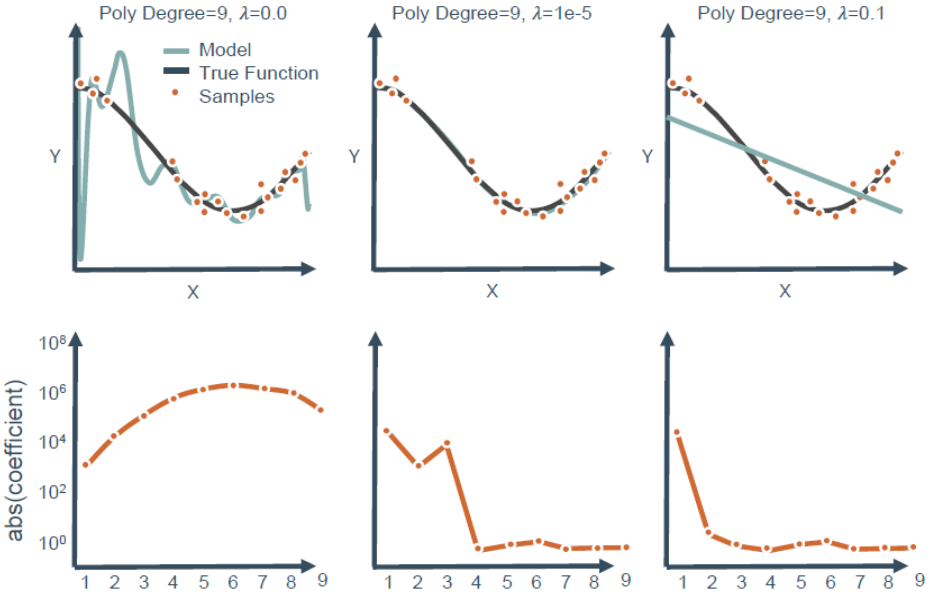
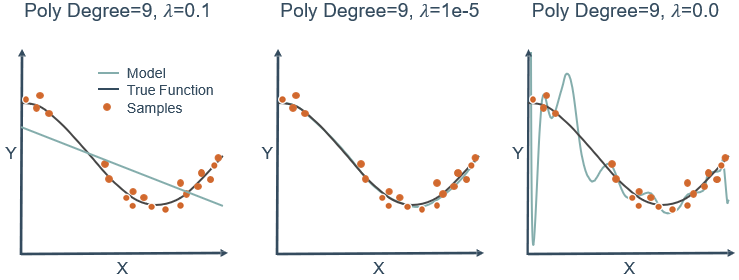
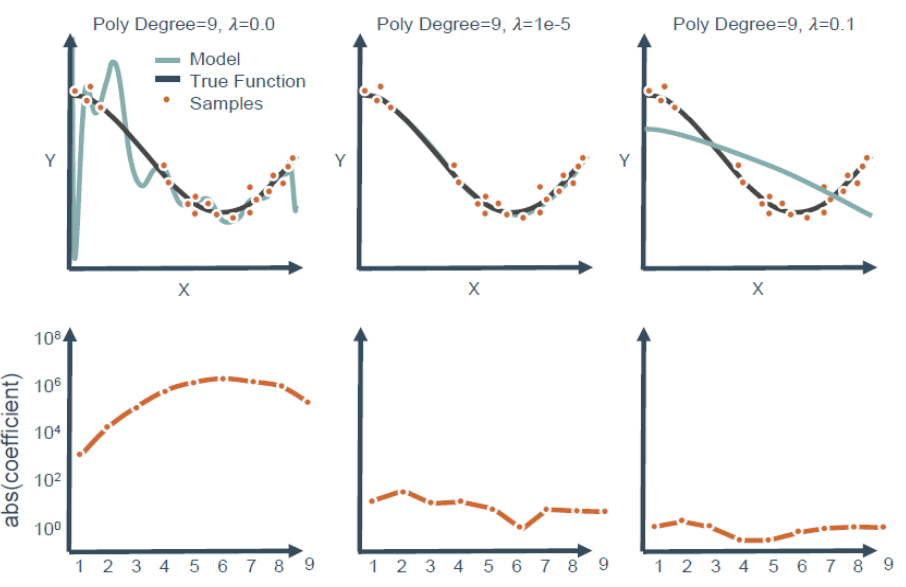
观察下图,可以看到3次多项式拟合的最好,但实际操作中不可能一下子就知道3次最好,都会往高次慢慢试,假设试到9次,那么如何用一个9次多项式拟合数据,并防止过拟合?
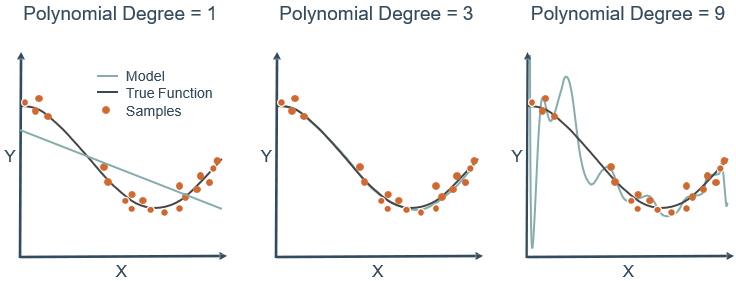
J
(
β
)
=
1
2
m
∑
i
=
1
m
(
y
β
(
x
(
i
)
)
−
y
(
i
)
)
2
J(\beta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(y_{\beta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}
J(β)=2m1i=1∑m(yβ(x(i))−y(i))2
答案是正则化(regularization)。采用正则化方法会自动削弱不重要特征,并自动从特征中提取出重要的特征,从而减少特征的个数。这个方法非常有效,当有很多特征时,其中每一个特征都能对预测产生一点影响。例如,在预测房价的例子中可以有很多特征,其中每个特征变量都是有用的,因此不希望删掉。这就导致了正则化概念的产生,即保留所有的特征,但是减小特征对应的参数值的大小。
正则化在机器学习中扮演着重要的角色,被用来解决经常出现的过拟合问题。在大部分机器学习模型的损失函数中,几乎都可以看到后面添加了一个额外项,即正则项(惩罚因子),用来缩小参数值。在线性回归模型的损失函数中,如果添加一个L1正则项,则称为套索(lasso)回归;如果添加一个L2正则化项,则称为岭(ridge)回归。
🕘 4.1 套索回归(L1)☆☆☆
Ll 正则化可以产生稀疏模型,即使得一些特征项的系数为0,因而可用于选择特征,只留下系数不为0的特征,在一定程度上防止出现过拟合。
J ( β ) = 1 2 m ∑ i = 1 m ( y β ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n ∣ β j ∣ J(\beta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(y_{\beta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\color{red}\lambda \sum_{j=1}^{n}\left|\beta_{j}\right| J(β)=2m1i=1∑m(yβ(x(i))−y(i))2+λj=1∑n∣βj∣
- 惩罚项有选择地收缩了某些系数(易产生0系数)
- 可以被用来做特征选择(多个线性相关特征保留其一)
补充知识:范数(线性代数的一个概念)
- L 1 L1 L1范数: ∑ j = 1 n ∣ β j ∣ \sum_{j=1}^{n}\left|\beta_{j}\right| ∑j=1n∣βj∣
表示向量中每个元素绝对值的和。根据定义,L1范数的计算分两步,首先逐个求得元素的绝对值,然后相加求和即可。- L 2 L2 L2范数: ∑ j = 1 n β j 2 \sum_{j=1}^{n} \beta_{j}^{2} ∑j=1nβj2
表示向量中每个元素的平方和的平方根。根据定义,L2范数的计算分三步,首先逐个求得元素的平方,然后相加求和,最后求和的平方根。
🕤 4.1.1 效果
🕤 4.1.2 分析
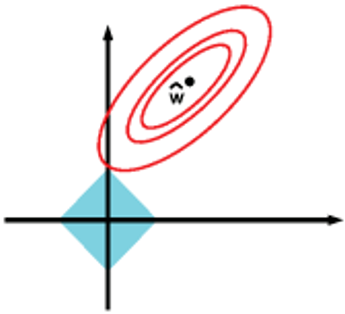
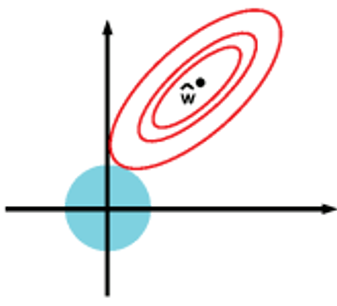
上图的环形等值线是
J
0
J_0
J0(原损失函数)的等值线,菱形是L1范数的图形。
J
0
J_0
J0等值线与
L
L
L首次相交的地方就是最优解。上图中
J
0
J_0
J0与
L
L
L在
L
L
L的一个顶点处相交,这个顶点就是最优解。注意这个顶点的值是
(
ω
1
,
ω
2
)
=
(
0
,
ω
)
(\omega_1,\omega_2)=(0,\omega)
(ω1,ω2)=(0,ω)。可以直观地想象,因为L函数有很多突出的角,
J
0
J_0
J0与这些顶角接触的概率会远大于与L其他部位接触的概率,而在这些角上会有很多系数值等于0,即L1正则化可以产生稀疏模型,进而可以用于特征选择。
🕤 4.1.3 语法
导入包含回归方法的类:
from sklearn.linear_model import Lasso
from sklearn.linear_model import LassoCV # 交叉验证
创建该类的一个对象:
LR = Lasso(alpha=1.0) # 正则化参数
LRcv = LassoCV(alphas=[1e-3, 1e-2, 1e-1, 1], cv=4) # LassoCV 使用交叉验证自动确定alpha的值
拟合训练数据,并在测试数据上预测:
LR = LR.fit(X_train, y_train)
y_predict = LR.predict(X_test)
LRcv = LRcv.fit(X_train, y_train)
y_predict = LRcv.predict(X_test)
在线文档:🔎 套索回归的语法
在线文档:🔎 套索回归交叉验证的语法
🕘 4.2 岭回归(L2)☆☆☆
J
(
β
)
=
1
2
m
∑
i
=
1
m
(
y
β
(
x
(
i
)
)
−
y
(
i
)
)
2
+
λ
∑
j
=
1
n
β
j
2
J(\beta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(y_{\beta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\color{red}\lambda \sum_{j=1}^{n} \beta_{j}^{2}
J(β)=2m1i=1∑m(yβ(x(i))−y(i))2+λj=1∑nβj2
- 惩罚项收缩了所有系数的大小(倾向于生成较小的系数)
- 越大的系数被惩罚得越多,因为惩罚的是平方
- 比套索回归收敛速度快
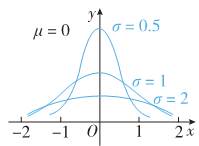
以正态分布
X
∼
N
(
μ
,
σ
2
)
X \sim N\left(\mu, \sigma^{2}\right)
X∼N(μ,σ2)做例子:
就相当于收缩
σ
\sigma
σ的大小
🕤 4.2.1 效果
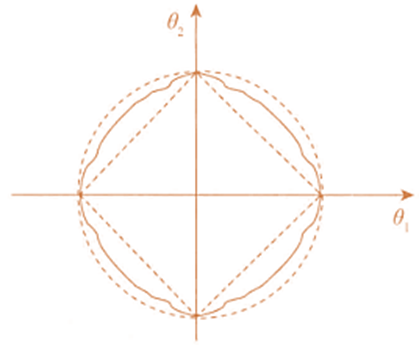
🕤 4.2.2 分析
二维平面下L2范数平方的函数图形是个圆,与菱形相比,被磨去了棱角。因此 J 0 J_0 J0与 L L L相交时, ω 1 \omega_1 ω1或 ω 2 \omega_2 ω2。等于零的概率小了许多,即L2正则化不具有稀疏性。
小结:L1会趋向于选择少量的特征,而使其他特征的系数都为0,而L2会选择更多的特征,这些特征的系数都会接近于0。模型拟合过程中通常倾向于让参数尽可能小,如果参数很大,只要数据偏移一点,就会对结果造成很大的影响;如果参数足够小,数据偏移得多一点也不会对结果造成什么影响。套索回归在特征选择时非常有用,而岭回归就只是一种正则化,L2范数可以防止过拟合,提升模型的泛化能力。
🕤 4.2.3 语法
导入包含回归方法的类:
from sklearn.linear_model import Ridge
from sklearn.linear_model import RidgeCV # 交叉验证
创建该类的一个对象:
RR = Ridge(alpha=1.0) # 正则化参数
RRcv = RidgeCV(alphas=[1e-3, 1e-2, 1e-1, 1], cv=4) # RidgeCV 使用交叉验证自动确定alpha的值
拟合训练数据,并在测试数据上预测:
RR = RR.fit(X_train, y_train)
y_predict = RR.predict(X_test)
RRcv = RRcv.fit(X_train, y_train)
y_predict = RRcv.predict(X_test)
在线文档:🔎 岭回归的语法
在线文档:🔎 岭回归交叉验证的语法
🕘 4.3 弹性网络回归(ElasticNet)
J ( β ) = 1 2 m ∑ i = 1 m ( y β ( x ( i ) ) − y ( i ) ) 2 + λ 1 ∑ j = 1 n ∣ β j ∣ + λ 2 ∑ j = 1 n β j 2 J(\beta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(y_{\beta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\color{red}\lambda_{1} \sum_{j=1}^{n}\left|\beta_{j}\right|+\lambda_{2} \sum_{j=1}^{n} \beta_{j}^{2} J(β)=2m1i=1∑m(yβ(x(i))−y(i))2+λ1j=1∑n∣βj∣+λ2j=1∑nβj2
- 岭回归和套索回归的综合,用以平衡稀疏和平滑两个问题
- 需要调节额外的参数,来分配L1和L2正则化惩罚项的比例
弹性网络回归的特点是:
(1)当多个特征和另一个特征相关时,套索回归倾向于随机选择其中一个,而弹性网络回归倾向于选择两个。
(2)弹性网络同时进行正则化与特征选择。
(3)当特征出现严重的多重共线性时,效果明显。
(4)当α接近0时,表现接近岭回归。
(5)当α从0变化到1时,目标函数的稀疏解(系数为0的情况)从0增加到套索回归的稀疏解。
🕤 4.3.1 语法
导入包含回归方法的类:
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import ElasticNetCV # 交叉验证
创建该类的一个对象:
EN = ElasticNet(alpha=1.0, l1_ratio=0.5) # l1_ratio把alpha的值分配给L1/L2
ENcv = ElasticNetCV(alphas=[1e-3, 1e-2, 1e-1, 1], cv=5) # ElasticNetCV 使用交叉验证自动确定alpha和l1_ratio的值
拟合训练数据,并在测试数据上预测:
EN = EN.fit(X_train, y_train)
y_predict = EN.predict(X_test)
ENcv = ENcv.fit(X_train, y_train)
y_predict = ENcv.predict(X_test)
在线文档:🔎 弹性网络回归的语法
在线文档:🔎 弹性网络回归交叉验证的语法
🕒 5. 超参数调优
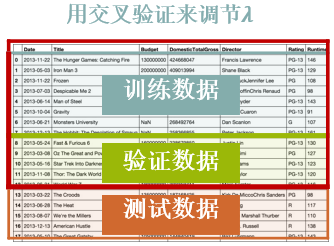
- 正则化系数( λ 1 \lambda_1 λ1 和 λ 2 \lambda_2 λ2)是根据经验决定的
- 想让模型泛化——不要使用测试数据集来调节 λ 1 \lambda_1 λ1 和 λ 2 \lambda_2 λ2
- 划分出另一个数据集来调节超参数——验证集(validation set)
🕒 6. 综合案例:波士顿房价预测
这个案例使用的数据集( Boston House Price Dataset)源自20世纪70年代中期美国人口普查局收集的美国马萨诸塞州波士顿住房价格有关信息。该数据集统计了当地城镇人均犯罪率、城镇非零售业务比例等共计13个指标(特征),第14个特征(相当于标签信息)给出了住房的中位数(均价)报价,共506个样例。
列号 列名 1 CRIM 城镇人均犯罪率 2 ZN 超过 25000 英尺的住宅用地所占比例 3 INDUS 城镇中非商业用地所占比例 4 CHAS 查理斯河哑变量(如果边界是河流, 为1; 否则为0) 5 NOX 一氧化氮浓度 6 RM 住宅的平均房间数 7 AGE 1940年以前建成的自住用房比例 8 DIS 距离 5 个波士顿就业中心的加权距离 9 RAD 距离高速公路的便利指数 10 TAX 每一万美元的不动产税率 11 PTRATIO 城镇中教师学生比例 12 B 城镇中黑人比例 13 LSTAT 地区有多少比例的房东属于低收人人群 14 MEDV 自住房的房屋均价(以千美元计) \begin{array}{|l|l|l|} \hline \text { 列号 } & {\text { 列名 }} & \\ \hline 1 & \text { CRIM } & \text { 城镇人均犯罪率 } \\ \hline 2 & \text { ZN } & \text { 超过 25000 英尺的住宅用地所占比例 } \\ \hline 3 & \text { INDUS } & \text { 城镇中非商业用地所占比例 } \\ \hline 4 & \text { CHAS } & \text { 查理斯河哑变量(如果边界是河流, 为1; 否则为0) } \\ \hline 5 & \text { NOX } & \text { 一氧化氮浓度 } \\ \hline 6 & \text { RM } & \text { 住宅的平均房间数 } \\ \hline 7 & \text { AGE } & \text { 1940年以前建成的自住用房比例 } \\ \hline 8 & \text { DIS } & \text { 距离 } 5 \text { 个波士顿就业中心的加权距离 } \\ \hline 9 & \text { RAD } & \text { 距离高速公路的便利指数 } \\ \hline 10 & \text { TAX } & \text { 每一万美元的不动产税率 } \\ \hline 11 & \text { PTRATIO } & \text { 城镇中教师学生比例 } \\ \hline 12 & \text { B } & \text { 城镇中黑人比例 } \\ \hline 13 & \text { LSTAT } & \text { 地区有多少比例的房东属于低收人人群 } \\ \hline 14 & \text { MEDV } & \text { 自住房的房屋均价(以千美元计) } \\ \hline \end{array} 列号 1234567891011121314 列名 CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT MEDV 城镇人均犯罪率 超过 25000 英尺的住宅用地所占比例 城镇中非商业用地所占比例 查理斯河哑变量(如果边界是河流, 为1; 否则为0) 一氧化氮浓度 住宅的平均房间数 1940年以前建成的自住用房比例 距离 5 个波士顿就业中心的加权距离 距离高速公路的便利指数 每一万美元的不动产税率 城镇中教师学生比例 城镇中黑人比例 地区有多少比例的房东属于低收人人群 自住房的房屋均价(以千美元计)
下面我们分别使用普通线性回归、岭回归和套索回归对波士顿房屋均价进行预测,并比较预测效果。
导入模块
# 获得普通线性模型、 岭回归模型、 套索回归模型
from sklearn.linear_model import LinearRegression, Ridge, Lasso
# 模型效果评估
from sklearn.metrics import r2_score
# 导入机器学习相关的数据集
import sklearn.datasets as datasets
# 法二:from sklearn.datasets import load_boston 只导入本次案例的数据集
获取训练数据
# 从datasets 模块中导入 boston 房价数据
boston=datasets.load_boston() # 这个boston是个字典类型的临时变量
# 法二:boston=load_boston()
data=boston.data
target=boston.target
boston.keys() # 我们可以用它的keys()方法输出它所包含的属性值。
#输出:dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename', 'data_module'])
关于数据集的keys()的介绍
在 sklearn 框架中,所有内置的数据集(比如鸢尾花、波士顿房价预测)都有这5个属性值。它们所代表的含义分别如下。
data:它不泛指数据,而是特指除标签之外的特征数据,针对波士顿房价数据集,它指的是前面的13个特征。target:本意是“目标”,这里是指标签( label)数据。针对波士顿房价数据集,就是指房价。feature_names:给出的实际上就是data对应的各个特征的名称。对于波士顿房价数据集而言,它指的就是影响房价的13个特征的名称。DESCR:是英文单词“description”的简写。顾名思义,它是对当前数据集的详细描述,有点类似于数据集的说明文档。比如,这个数据从哪里来,它有什么特征,每个特征是什么数据类型,如果引用数据集该引用哪些论文,等等。filename:说明的是这个数据集的名称,以及在当前计算机中的存储路径。另外、在 sklearn 中还常有不成文的约定:通常用大写的
X表示特征(这里共有13个),而用小写的y表示预测的目标(标签,这里有1个)。
处理数据。把数据集拆分成训练集和测试集
# X_train, X_test, y_train, y_true = train_test_split(X, y, test_size=0.30)
# 训练数据
X_train=data[:481] # 前480行作为训练集
Y_train=target[:481]
# 测试数据
x_test=data[481: ] # 第481行到506行作为测试集,进行模型预测和评估。
y_true=target[481: ]
创建机器学习模型
line=LinearRegression( ) # 普通线性回归
# line1=LinearRegression(normalize=True)
ridge=Ridge( ) # 岭回归,默认正则项惩罚系数alpha=1
# ridge1=Ridge(alpha=2.O)
lasso=Lasso( ) # 套索回归
# lasso1=Lasso(alpha=2.0)
训练和预测。将三个模型分别在训练集上进行训练,并在测试集上预测得到结果
# 训练
line.fit(X_train, Y_train)
ridge.fit(X_train, Y_train)
lasso.fit(X_train, Y_train)
# 预测
line_y_pre = line.predict(x_test)
ridge_y_pre = ridge.predict(x_test)
lasso_y_pre = lasso.predict(x_test)
绘制图形。将三个模型预测出的房价分别绘制在同一个线图中,并和真实的房价比较
import matplotlib.pyplot as plt
plt.plot(y_true, label= 'True') # 原始房价
plt.plot(line_y_pre, label= 'Line') # 普通线性回归预测的房价
plt.plot(ridge_y_pre, label= 'Ridge') # 岭回归预测的房价
plt.plot(lasso_y_pre, label= 'Lasso') # 套索回归预测的房价
plt.legend()
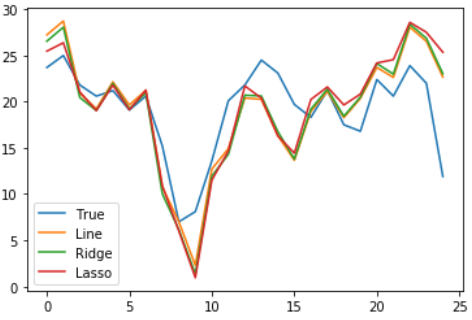
对比3个回归模型对房价的预测,可以简单地看出Line线更靠近原始数据,且趋势也符合原始数据,所以我们可以简单地判断普通线性回归模型在这里效果更好。为了进一步确认哪个模型更好,需要计算某种评价指标(如判定系数 R 2 R_2 R2),再进行对比
假设我们有测试数据集: [ y 1 x 11 x 12 ⋯ x 1 m y 2 x 21 x 22 ⋯ x 2 m ⋮ ⋮ ⋮ ⋮ y n x n 1 x 31 ⋯ x m n ] {\left[\begin{array}{ccccc} y_{1} & x_{11} & x_{12} & \cdots & x_{1 m} \\ y_{2} & x_{21} & x_{22} & \cdots & x_{2 m} \\ \vdots & \vdots & \vdots & & \vdots\\ y_{n} & x_{n 1} & x_{31} & \cdots & x_{m n} \end{array}\right]} ⎣⎢⎢⎢⎡y1y2⋮ynx11x21⋮xn1x12x22⋮x31⋯⋯⋯x1mx2m⋮xmn⎦⎥⎥⎥⎤,其中y是真实值,x是各特征值。
可以定义如下指标(其中 y ˉ \bar{y} yˉ是真实值的平均值):
- 总离差平方和(SST): ∑ i = 1 n ( y i − y ˉ ) 2 \sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2} ∑i=1n(yi−yˉ)2,体现真实值 y 1 , y 2 , ⋯ , y n y_{1}, y_{2}, \cdots, y_{n} y1,y2,⋯,yn偏离其平均值的总波动大小。
- 回归平方和(SSR): ∑ i = 1 n ( y ^ i − y ˉ ) 2 \sum_{i=1}^{n}\left(\hat{y}_{i}-\bar{y}\right)^{2} ∑i=1n(y^i−yˉ)2,是预测值 y ^ 1 , y ^ 2 , ⋯ , y ^ n \hat{y}_{1}, \hat{y}_{2}, \cdots, \hat{y}_{n} y^1,y^2,⋯,y^n,偏离真实值的平均值的总波动大小,也称为解释平方和。
- 残差平方和(SSE): ∑ i = 1 n ( y i − y ^ i ) 2 \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2} ∑i=1n(yi−y^i)2,是真实值 y 1 , y 2 , ⋯ , y n y_{1}, y_{2}, \cdots, y_{n} y1,y2,⋯,yn与预测值 y ^ 1 , y ^ 2 , ⋯ , y ^ n \hat{y}_{1}, \hat{y}_{2}, \cdots, \hat{y}_{n} y^1,y^2,⋯,y^n的误差平方和。
- 判定系数( R 2 R^2 R2): R 2 = S S R S S T = 1 − S S E S S T R^{2}=\frac{S S R}{S S T}=1-\frac{S S E}{S S T} R2=SSTSSR=1−SSTSSE,表示因变量Y的变异中有多少百分比可由自变量X的变异来解释,也叫拟合优度、可决系数。
判定系数 R 2 R^2 R2越接近于1,模型的拟合优度越高。拟合优度越大,意味着自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比高,观察点在回归直线附近越密集。下面分别计算三个模型在测试数据集上的判定系数,以比较三个模型的预测效果。
line_score = r2_score(y_true, line_y_pre)
ridge_score = r2_score(y_true, ridge_y_pre)
lasso_score = r2_score(y_true, lasso_y_pre)
print(line_score, ridge_score, lasso_score)
0.2926458566928456 0.2430119943999447 0.12157928259797934 0.2926458566928456 \quad 0.2430119943999447 \quad 0.12157928259797934 0.29264585669284560.24301199439994470.12157928259797934
由上面得到的 R 2 R^2 R2值可以看出,预测波士顿房价时,用普通线性回归模型比其他两个模型要好,而岭回归比套索回归模型稍好一些。
🕒 7. 逻辑回归
🕘 7.1 概念
逻辑回归(Logistic regression)算法,虽然名称中含有“回归”二字,却是一个分类算法。回归与分类的区别在于:回归预测的目标变量的取值是连续的(例如房屋的价格),可以用一条直线拟合,例如一元或多元线性回归模型;分类所预测的目标变量是类别型变量;取值是离散的,例如判断邮件是否为垃圾邮件、判断鸢尾花的类型等。有的书上逻辑回归又叫“对数几率回归”,博主认为叫“Logistic分类”更贴切些。
对于癌症病人治疗5年之后的状况这个例子,思考一下可以用线性回归做分类吗?
y
β
(
x
)
=
β
0
+
β
1
x
y_{\beta}\left(x\right)=\beta_{0}+\beta_{1} x
yβ(x)=β0+β1x
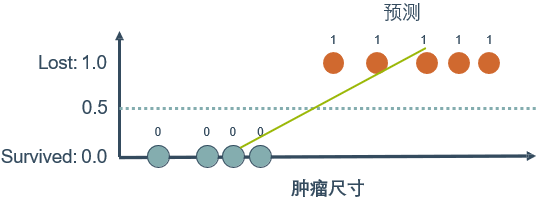
这样看似乎可行,但是如果又观测到许多大尺寸的恶性肿瘤,将其作为实例加入到训练集中来,做完线性回归后发现,再使用0.5作为阈值来预测肿瘤是良性还是恶性便不合适了。
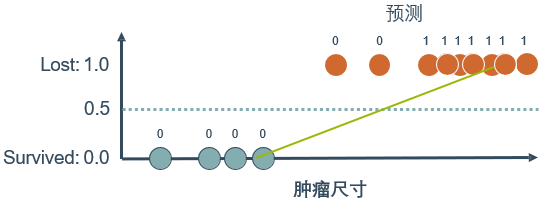
所以需要引入一个新的模型——逻辑回归,该模型的输出变量范围始终在0~1之间。逻辑回归模型的假设是:
h
β
(
x
)
=
g
(
z
)
h_{\beta}\left(x\right)=g(z)
hβ(x)=g(z),其中g代表逻辑(logistic)函数(又叫对数几率函数),
z
=
β
0
+
β
1
x
z=\beta_{0}+\beta_{1} x
z=β0+β1x,一个常用的逻辑函数为S形函数(sigmoid function),即
g
(
z
)
=
1
1
+
e
−
z
g(z)=\frac{1}{1+e^{-z}}
g(z)=1+e−z1,如图
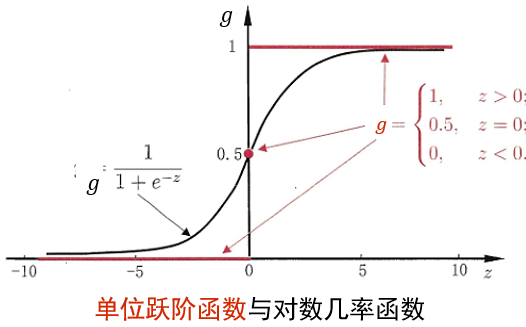
联立两式,得出
h
β
(
x
)
=
1
1
+
e
−
(
β
0
+
β
1
x
)
h_{\beta}(x)=\frac{1}{1+e^{-(\beta_{0}+\beta_{1} x)}}
hβ(x)=1+e−(β0+β1x)1
再把这个应用到上面的例子
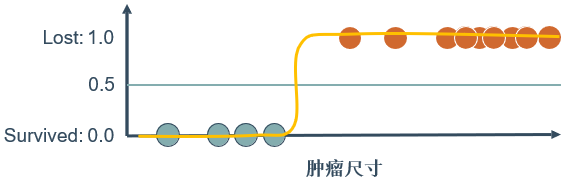
逻辑回归和线性回归的关系: β 0 + β 1 x = log [ h ( x ) 1 − h ( x ) ] \beta_{0}+\beta_{1} x=\log \left[\frac{h(x)}{1-h(x)}\right] β0+β1x=log[1−h(x)h(x)]
优点:
- 直接对分类可能性建模,无需事先假设数据分布
- 不是仅预测出“类别”,还可得到对近似概率的预测
- 对数几率函数是任意阶可导的凸函数,有很好的数学性质
🕘 7.2 判定边界(决策边界)
🕤 7.2.1 一个特征两个标签
一个特征(肿瘤尺寸)
两个类标签(survived, lost)
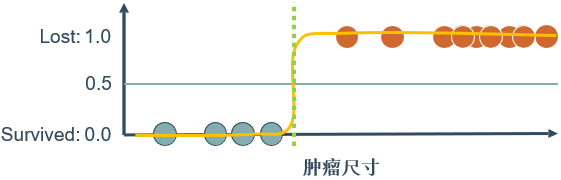
🕤 7.2.2 两个特征两个标签(二元分类)
两个特征(肿瘤尺寸,Age)
两个类标签(survived, lost)
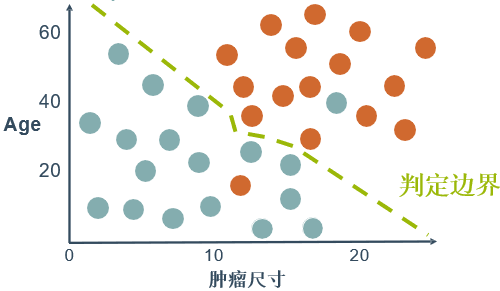
问题:如果数据呈现的分布情况如下图所示,什么样的模型才适合呢?
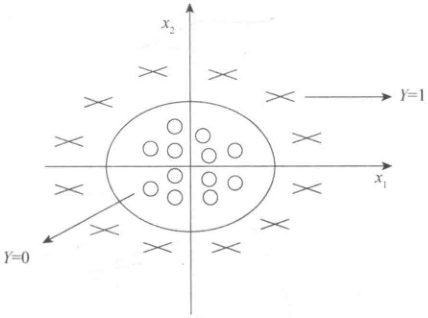
近似一个圆的曲线才能分隔
Y
=
0
Y=0
Y=0和
Y
=
1
Y=1
Y=1的区域,所以需要二次方特征,例如
h
β
(
X
)
=
g
(
β
0
+
β
1
x
1
+
β
2
x
2
+
β
3
x
1
2
+
β
4
x
2
2
)
h_{\beta}(X)=g\left(\beta_{0}+\beta_{1} x_{1}+\beta_{2} x_{2}+\beta_{3} x_{1}^{2}+\beta_{4} x_{2}^{2}\right)
hβ(X)=g(β0+β1x1+β2x2+β3x12+β4x22)。假设参数
β
\beta
β是
[
−
1
0
0
0
1
1
]
T
[-1 \ 0 \ 0 \ 0 \ 1 \ 1]^{T}
[−1 0 0 0 1 1]T,则得到的判定边界恰好是圆心在原点且半径为1的圆形。我们可以用复杂的逻辑回归模型来得到非结构性可分数据的判定边界,解决二元分类问题。
🕤 7.2.3 两个特征三个标签(多分类)
两个特征(肿瘤尺寸,Age)
两个类标签(survived, complications, lost)
逻辑回归本身是一个二分类器,用二分类器解决多分类问题的基本思想是“拆解法”,即将多分类任务拆分为若干个二分类任务求解。常用的拆解法有三种:一对一(one vs. one,OvO)、一对其余(one vs. rest,OvR)(一对其余,下图)和多对多(many vs. many,MvM)。
- 一对一策略将N个类别两两组合,例如有 C i C_i Ci和 C j C_j Cj,两个类,为区别类别 C i C_i Ci和 C j C_j Cj,训练一个二分类器(如逻辑回归),该分类器把D中的 C i C_i Ci类样例作为正例, C j C_j Cj类样例作为反例,所以共需训练N(N一1)/2个二分类器。在测试阶段,新样例需要同时提交给所有分类器,最终预测结果是被预测得最多的类别。
- 一对其余策略是每次将一个类的样例作为正例,其他所有类的样例作为反例来训练N个分类器。在测试时若仅有一个分类器预测为正类,则对应的类别标记作为最终分类结果;若有多个分类器预测为正类,则通常考虑各分类器的预测置信度(如逻辑回归模型输出的概率值),选择置信度最大的类别作为分类的结果。
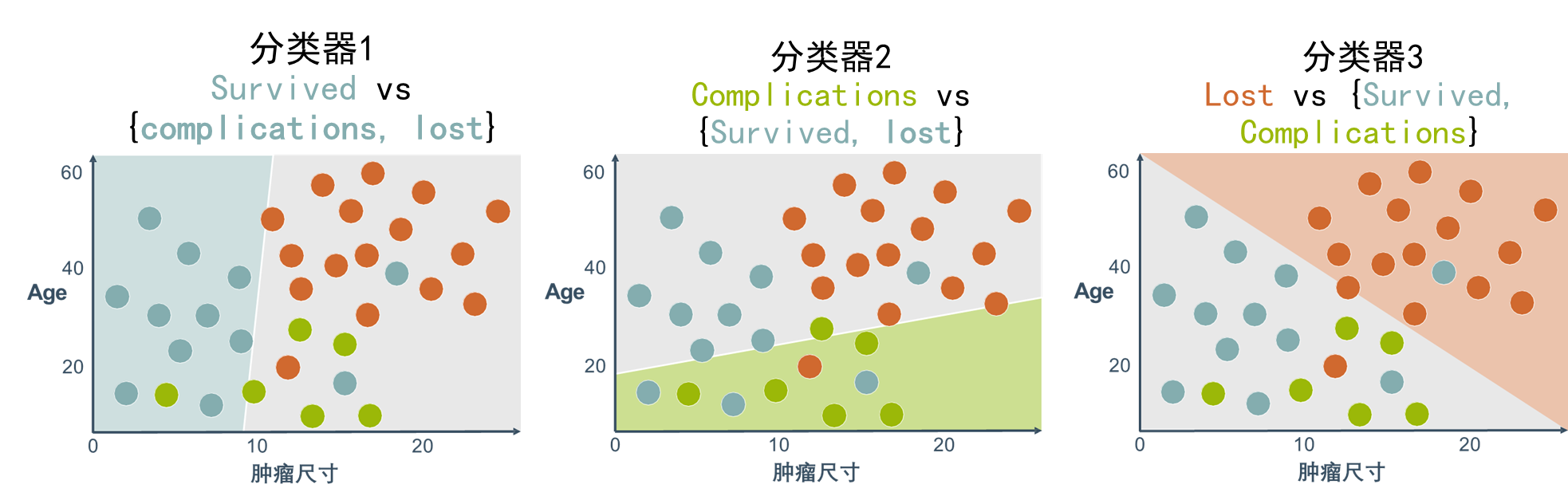
- 多对多策略每次将若干个类作为正类,若干个其他类作为反类。显然,一对一和一对其余是多对多的特例。正反类的划分必须有特殊的设计,不能随意选取。一种最常用的多对多技术是纠错输出码(error correcting output codes,ECOC),详见周志华的《机器学习》一书。
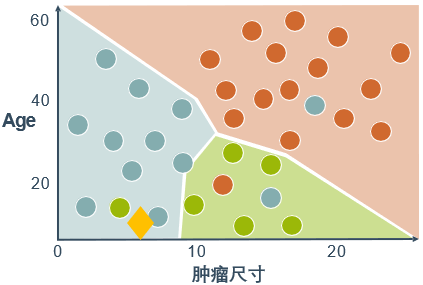
每个区域属于其概率最大的类
(例如:新样例(黄色菱形)同属分类器1、2的正样例,但分类器1的输出概率更高,所以将其划分为Survive类)
🕘 7.3 损失函数
对于线性回归模型,定义的损失函数是所有误差的平方和。理论上来说,也可以对逻辑回归模型沿用这个损失函数,但问题是将 h β ( x ) = 1 1 + e − ( β 0 + β 1 x ) h_{\beta}(x)=\frac{1}{1+e^{-(\beta_{0}+\beta_{1} x)}} hβ(x)=1+e−(β0+β1x)1代入到这样的损失函数中时,得到的将是一个非凸函数(non-convex function),这意味着损失函数有许多局部最小值,不能保证找到全局最小值。
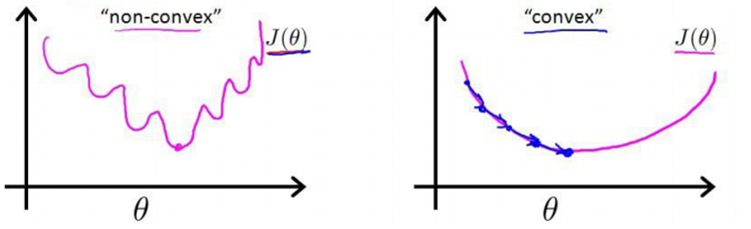
因此需要重新定义逻辑回归的损失函数为:
J
(
β
)
=
1
m
∑
i
=
1
m
Cost
(
h
β
(
x
(
i
)
)
,
y
(
i
)
)
J(\beta)=\frac{1}{m} \sum_{i=1}^{m} \operatorname{Cost}\left(h_{\beta}\left(x^{(i)}\right), y^{(i)}\right)
J(β)=m1i=1∑mCost(hβ(x(i)),y(i))
式中,
Cost
(
h
β
(
x
)
,
y
)
=
\operatorname{Cost}\left(h_{\beta}(x), y\right)=
Cost(hβ(x),y)=
−
log
(
h
β
(
x
)
)
,
if
y
=
1
−
log
(
1
−
h
β
(
x
)
)
,
if
y
=
0
{\begin{array}{ll} -\log \left(h_{\beta}(x)\right), & \text { if } \mathrm{y}=1 \\ -\log \left(1-h_{\beta}(x)\right), & \text { if } \mathrm{y}=0 \end{array}}
−log(hβ(x)),−log(1−hβ(x)), if y=1 if y=0。这样构建的
Cost
(
h
β
(
x
)
,
y
)
\operatorname{Cost}\left(h_{\beta}(x), y\right)
Cost(hβ(x),y)函数的特点是:
- 当实际 y = 1 y=1 y=1且 h β h_{\beta} hβ。也为1时,损失为0;当y=1但 h β h_{\beta} hβ不为1时,损失会随着 h β h_{\beta} hβ的变小而变大,即真实值与预测值差距变大。
- 当实际 y = 0 y=0 y=0且 h β h_{\beta} hβ也为0时,损失为0;当y=0但 h β h_{\beta} hβ不为0时,损失会随着 h β h_{\beta} hβ的变大而变大,即真实值与预测值差距变大,也可以更容易判断模型的好坏。
可以将构建的
Cost
(
h
β
(
x
)
,
y
)
\operatorname{Cost}\left(h_{\beta}(x), y\right)
Cost(hβ(x),y)函数等价地写成如下形式:
Cost
(
h
β
(
x
)
,
y
)
=
−
y
×
log
(
h
β
(
x
)
)
−
(
1
−
y
)
×
log
(
1
−
h
β
(
x
)
)
\operatorname{Cost}\left(h_{\beta}(x), y\right)=-y \times \log \left(h_{\beta}(x)\right)-(1-y) \times \log \left(1-h_{\beta}(x)\right)
Cost(hβ(x),y)=−y×log(hβ(x))−(1−y)×log(1−hβ(x))
代入到上面公式中,得到逻辑回归的损失函数
J
(
β
)
J(\beta)
J(β)的表达式如下:
J
(
β
)
=
−
1
m
[
∑
i
=
1
m
y
(
i
)
log
h
β
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
h
β
(
x
(
i
)
)
)
]
J(\beta)=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\beta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\beta}\left(x^{(i)}\right)\right)\right]
J(β)=−m1[i=1∑my(i)loghβ(x(i))+(1−y(i))log(1−hβ(x(i)))]
对线性回归,可以通过对损失函数增加正则项来防止过拟合。同样对于逻辑回归,也可以给损失函数增加正则化项,例如,增加一个L2正则化项,整体损失函数的表达式则变为:
J ( β ) = − 1 m [ ∑ i = 1 m y ( i ) log ( h β ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h β ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n β j 2 J(\beta)=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log \left(h_{\beta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\beta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \beta_{j}^{2}\right. J(β)=−m1[i=1∑my(i)log(hβ(x(i))+(1−y(i))log(1−hβ(x(i)))]+2mλj=1∑nβj2
f ( y ) = p y ( 1 − p ) 1 − y = { p , y = 1 1 − p , y = 0 p i = h w ( z i ) = h w ( w T x i ) \begin{array}{l} f(y)=p^{y}(1-p)^{1-y}=\left\{\begin{array}{c} p, y=1 \\ 1-p, y=0 \end{array}\right. \\ p_{i}=h_{w}\left(z_{i}\right)=h_{w}\left(w^{\mathrm{T}} x_{i}\right) \end{array} f(y)=py(1−p)1−y={p,y=11−p,y=0pi=hw(zi)=hw(wTxi)
🕘 7.4 语法
导入包含分类方法的类:
from sklearn.linear_model import LogisticRegression
创建该类的一个实例:
LR = LogisticRegression(penalty = 'l2', C = 10.0)
# 正则化参数 penalty -惩罚项,为 ‘l2‘或’l1’;c-正则化系数λ的倒数,越小正则化越强
拟合训练数据并预测:
LR = LR.fit(X_train, y_train)
y_predict = LR.predict(X_test)
在线文档:🔎 逻辑回归的语法
使用交叉验证自动确定正则化参数:LogisticRegressionCV
❗ 转载请注明出处
作者:HinsCoder
博客链接:🔎 作者博客主页
🕒 8. 线性回归和逻辑回归的异同
相同点:
(1)线性回归和逻辑回归都是有监督学习算法。
(2)线性回归和逻辑回归的损失函数、正则化的数学原理与形式基本类似。
不同点:
(1)线性回归用于解决回归问题,逻辑回归用于解决分类问题。
(2)线性回归要求目标变量是连续数值型,逻辑回归要求是离散型。
(3)线性回归要求特征与目标变量呈线性关系,逻辑回归不要求特征与目标变量呈线性关系。
🕒 9. 分类评价指标
🕘 9.1 精度指标的局限性
- 要求你为白血病的诊断构建一个分类器
- 训练数据:1% 的样例患有白血病,99% 是健康的
- 评价指标是预测精度:即预测正确的百分比
- 那么构建一个最简单的分类器,对所有输入都回答“健康”,仍然可以达到99%的精度…
现实中样本在不同类别的分布不平衡,导致精度不能很好地反应分类器的性能
🕘 9.2 混淆矩阵☆☆☆
混淆矩阵(confusion matrix)是对分类模型进行性能评价的重要工具。它是总结分类模型预测结果的情形分析表,以矩阵形式将数据集中的记录按照真实的类别与分类模型做出的分类判断进行汇总。
以二分类问题为例,数据集本身存在正例和负例两类记录,将学习器预测类别与数据集本身的数据类别进行比较,根据学习器预测结果的对错,将会产生真、假两类判断记录。二分类问题的混淆矩阵是一个2×2的情形分析表,显示以下四组记录的数目:正确判断的正例记录(真正例)(Ture Positive)、错误判断的正例记录(假正例)(False Positive)、正确判断的负例记录(真负例)(Ture Negative)以及错误判断的负例记录(假负例)(False Negative)。

以核酸检测为例,真阳性(正例)和假阳性分别是病人和健康人的化验结果呈阳性,而真阴性(负例)和假阴性分别是健康人和病人的化验结果呈阴性。显然,分类模型对在混淆矩阵对角线上的真阳性和真阴性记录做出了正确的分类,而对反对角线上的假阳性和假阴性记录发生了误判。
常用指标:
- 精度(Accuracy)(预测正确的比例): A = T P + T N T P + F N + F P + T N \text {A}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{FN}+\mathrm{FP}+\mathrm{TN}} A=TP+FN+FP+TNTP+TN
- 错误率: Error = 1 - A \text { Error }=1 \text { - A } Error =1 - A
由混淆矩阵可以计算真正例率、假正例率、真负例率、假负例率、查准率、查全率和F指标等各种评价指标。
特别是混淆矩阵区分了假正例和假负例两种不同性质的误判,可以用来估计分类模型误判造成的期望损失。
🕘 9.3 查准率与查全率、P-R曲线与F1分数☆☆☆
查准率(precision,P),又叫准确率。查准率是针对预测结果而言的,它表示的是预测为正的样例中有多少是真正的正样例(比如:核酸检测的阳性未必是真的阳性)。
P
=
T
P
T
P
+
F
P
\text { P }=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}
P =TP+FPTP
查全率(recall,R),又叫召回率,敏感度(sensitivity)。查全率是针对原来的样本而言的,它表示的是样本中的正例有多少被预测正确(比如:核酸检测的某些阳性样本没有被检测出来)。
R = T P T P + F N \text { R }=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} R =TP+FNTP
查准率和查全率是一对矛盾的度量。一般来说,查准率高时,查全率往往偏低;查全率高时,查准率往往偏低。可以这样理解,在一个分类器中,你想要更高的查准率,那么阈值要设置得更高,只有这样才能有较高的把握确定预测的正例是真正例。但如果把阈值设置高了,那预测出正例的样本数就少了,真正例数就更少了,查不全所有的正样例。
例如,华强希望将熟瓜尽可能多地选出来,则可通过增加选瓜的数量来实现,如果将所有的西瓜都选上,所有的熟瓜也必然都被选上,但这样查准率就会比较低;若希望选出的瓜中熟瓜的比例尽可能高,则可只挑选最有把握的瓜,比如问问瓜摊老板,但这样难免会漏掉不少熟瓜,查全率较低,况且也可能选出生瓜蛋子,导致“萨日朗”~~。通常只有在一些简单的任务中,才可能使查全率和查准率都很高。
拓展:特异度(Specificity)
S = T N F P + T N \text { S }=\frac{\mathrm{TN}}{\mathrm{FP}+\mathrm{TN}} S =FP+TNTN
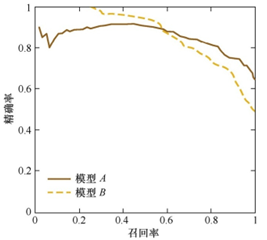
在很多情形下,我们可根据学习器的预测结果对样例进行排序,排在前面的是学习器认为“最可能”是正例的样本,排在最后的则是学习器认为“最不可能”是正例的样本。按此顺序逐个把样本作为正例进行预测,则每次可以计算出当前的查全率、查准率。以查准率为纵轴、查全率为横轴作图,就得到了查准率-查全率曲线,简称“P-R曲线”,显示该曲线的图称为“P-R图”,如下图
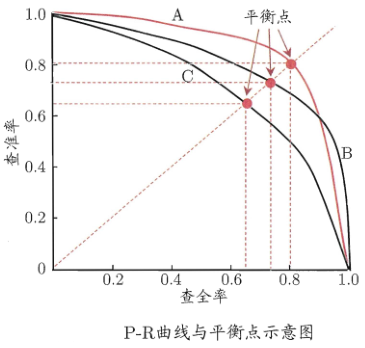
注:为绘图方便和美观,示意图显示出单调平滑曲线;但现实任务中的P-R曲线常是非单调、不平滑的,在很多局部有上下波动。实际参见下图:
P-R图直观地显示出学习器在样本总体上的查全率、查准率,在进行比较时,若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者,例如上图中学习器A的性能优于学习器C;如果两个学习器的P-R曲线发生了交叉,例如图中的A与B,则难以一般性地断言两者孰优孰劣,只能在具体的查准率或查全率条件下进行比较。然而,在很多情形下,人们往往仍希望把学习器A与B比出个高低,这时一个比较合理的判据是比较P-R曲线下面积的大小,它在一定程度上表征了学习器在查准率和查全率上取得相对“双高”的比例。但这个值不太容易估算,因此,人们设计了一些综合考虑查准率、查全率的性能度量。
“平衡点”(Break-Event Point,简称BEP)就是这样一个度量,它是“查准率=查全率”时的取值,例如图中学习器C的BEP是0.64,而基于BEP的比较,可认为学习器A优于B。
但BEP还是过于简化了些,更常用的是F1度量:
F 1 F1 F1分数是查准率与查全率的调和平均(harmonic mean)数,其定义为:
1 F 1 = 1 2 ( 1 P + 1 R ) \frac{1}{F 1}=\frac{1}{2}\left(\frac{1}{P}+\frac{1}{R}\right) F11=21(P1+R1)
这样可以避免出现查全率或查准率一个为1而另一个为0的极端情况,另外
F
1
F1
F1分数综合了查准率Р和查全率R的结果,它的取值在0~1之间,当
F
1
F1
F1较高时说明结果比较理想。
F
1
F1
F1计算公式为:
F
1
=
2
×
P
×
R
P
+
R
=
2
×
T
P
2
T
P
+
F
P
+
F
N
F 1=\frac{2 \times P \times R}{P+R}=\frac{2 \times T P}{2T P+FP+FN}
F1=P+R2×P×R=2TP+FP+FN2×TP
在一些应用中,对查准率和查全率的重视程度有所不同,例如在淘宝中,更希望大数据推荐的内容是用户感兴趣的,此时查准率更重要;而在健康码系统中,更希望尽可能少漏掉感染者,从而根据时空判断密接者并赋码管理,此时查全率更重要。
F
1
F1
F1度量的一般形式——
F
β
F_\beta
Fβ,能让我们表达出对查准率/查全率的不同偏好,它定义为:
1
F
β
=
1
1
+
β
2
(
1
P
+
β
2
R
)
\frac{1}{F_{\beta}}=\frac{1}{1+\beta^2}\left(\frac{1}{P}+\frac{\beta^2}{R}\right)
Fβ1=1+β21(P1+Rβ2)
F
β
F_\beta
Fβ的计算公式为:
F
β
=
(
1
+
β
2
)
×
P
×
R
(
β
2
×
P
)
+
R
F_{\beta}=\frac{\left(1+\beta^{2}\right) \times P \times R}{\left(\beta^{2} \times P\right)+R}
Fβ=(β2×P)+R(1+β2)×P×R
其中 β > 0 \beta>0 β>0度量了查全率对查准率的相对重要性
- β = 1 \beta = 1 β=1时退化为标准的 F 1 F1 F1;
- β > 1 \beta > 1 β>1时查全率有更大影响;
- β < 1 \beta < 1 β<1时查准率有更大影响。
🕘 9.4 宏平均和微平均☆☆☆
我们将上述的二分类问题推广到多分类问题,我们希望在n个二分类混淆矩阵上综合考察查准率和查全率
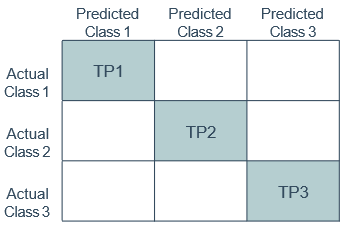
Accuracy
=
T
P
1
+
T
P
2
+
T
P
3
Total
\text { Accuracy }=\frac{\mathrm{TP} 1+\mathrm{TP} 2+\mathrm{TP} 3}{\text { Total }}
Accuracy = Total TP1+TP2+TP3
一种直接的做法是先在各混淆矩阵上分别计算出查准率和查全率,记为 ( P 1 , R 1 ) , ( P 2 , R 2 ) , . . . , ( P n . , R n ) (P_1,R_1),(P_2, R_2),... , (P_n.,R_n) (P1,R1),(P2,R2),...,(Pn.,Rn),再计算平均值,这样就得到“宏查准率”(macro-P)、“宏查全率”(macro-R),以及相应的“宏F1”(macro-F1):
macro- P = 1 n ∑ i = 1 n P i macro- R = 1 n ∑ i = 1 n R i \text { macro- } P=\frac{1}{n} \sum_{i=1}^{n} P_{i} \\ \text { macro- } R=\frac{1}{n} \sum_{i=1}^{n} R_{i} macro- P=n1i=1∑nPi macro- R=n1i=1∑nRi
macro- F 1 = 1 n ∑ i = 1 n F 1 i = 2 × macro- P × macro- R macro- P + macro- R \text { macro- } \mathrm{F1}=\frac{1}{n} \sum_{i=1}^{n} F 1_{i} =\frac{2 \times \text { macro- } P \times \text { macro- } R}{\text { macro- } P+\text { macro- } R} macro- F1=n1i=1∑nF1i= macro- P+ macro- R2× macro- P× macro- R
还可先将各混淆矩阵的对应元素进行平均,得到 T P 、 F P 、 T N 、 F N TP、FP、TN、FN TP、FP、TN、FN的平均值,分别记为 T P ‾ , F P ‾ , T N ‾ , F N ‾ \overline{T P}, \overline{F P}, \overline{T N}, \overline{F N} TP,FP,TN,FN,再基于这些平均值计算出“微查准率”(micro-P)、“微查全率”(micro-R)和“微F1”(micro-F1):
micro-
P
=
T
P
‾
T
P
‾
+
F
P
‾
micro-
R
=
T
P
‾
T
P
‾
+
F
N
‾
\text { micro- } P=\frac{\overline{T P}}{\overline{T P}+\overline{F P}} \\ \text { micro- } R=\frac{\overline{T P}}{\overline{T P}+\overline{F N}}
micro- P=TP+FPTP micro- R=TP+FNTP
micro-
F
1
=
2
×
micro-
P
×
micro-
R
micro-
P
+
micro-
R
\text { micro- } F 1=\frac{2 \times \text { micro- } P \times \text { micro- } R}{\text { micro- } P+\text { micro- } R}
micro- F1= micro- P+ micro- R2× micro- P× micro- R
宏平均(Macro-averaging)与微平均(Micro-averaging)的不同之处在于:宏平均赋予每个混淆矩阵相同的权重,然而微平均赋予每个样本决策相同的权重。在微平均评估指标中,样本数多的类别主导着样本数少的类。
m i c r o − F 1 = m i c r o − p r e c i s i o n = m i c r o − r e c a l l = a c c u r a c y micro-F1 = micro-precision = micro-recall = accuracy micro−F1=micro−precision=micro−recall=accuracy
练习题☆☆☆
假设有10个样本,属于A、B、C三个类别。假设这10个样本的真实类别和预测的类别分别是:
真实:A A A C B C A B B C
预测:A A C B A C A C B C
1、求出每个类别的P, R, 和F1
2、求出宏平均P, R, 和F1
3、求出微平均P, R, 和F1解答:
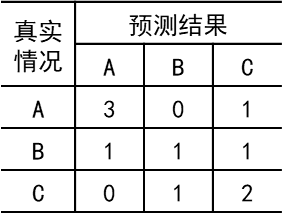
首先画出混淆矩阵:
1、查准率: P A = 3 3 + 1 + 0 = 3 4 P B = 1 0 + 1 + 1 = 1 2 P C = 2 1 + 1 + 2 = 1 2 P_A=\frac{3}{3+1+0}=\frac{3}{4} \quad P_B=\frac{1}{0+1+1}=\frac{1}{2} \quad P_C=\frac{2}{1+1+2}=\frac{1}{2} PA=3+1+03=43PB=0+1+11=21PC=1+1+22=21
查全率: R A = 3 3 + 0 + 1 = 3 4 R B = 1 1 + 1 + 1 = 1 3 R C = 2 0 + 1 + 2 = 2 3 R_A=\frac{3}{3+0+1}=\frac{3}{4} \quad R_B=\frac{1}{1+1+1}=\frac{1}{3} \quad R_C=\frac{2}{0+1+2}=\frac{2}{3} RA=3+0+13=43RB=1+1+11=31RC=0+1+22=32
F1: F 1 A = 2 × P A × R A P A + R A = 3 4 F1_A=\frac{2 \times P_A \times R_A}{P_A+R_A}=\frac{3}{4} F1A=PA+RA2×PA×RA=43
F 1 B = 2 × P B × R B P B + R B = 2 5 F1_B=\frac{2 \times P_B \times R_B}{P_B+R_B}=\frac{2}{5} F1B=PB+RB2×PB×RB=52
F 1 C = 2 × P C × R C P C + R C = 4 7 F1_C=\frac{2 \times P_C \times R_C}{P_C+R_C}=\frac{4}{7} F1C=PC+RC2×PC×RC=74
2、
macro- P = 1 3 ∑ i = 1 3 P i = 1 3 × ( 3 4 + 1 2 + 1 2 ) = 7 12 \text { macro- } P=\frac{1}{3} \sum_{i=1}^{3} P_{i} = \frac{1}{3} \times (\frac{3}{4}+\frac{1}{2}+\frac{1}{2})=\frac{7}{12} macro- P=31∑i=13Pi=31×(43+21+21)=127
macro- R = 1 3 ∑ i = 1 3 R i = 1 3 × ( 3 4 + 1 3 + 2 3 ) = 7 12 \text { macro- } R=\frac{1}{3} \sum_{i=1}^{3} R_{i} = \frac{1}{3} \times (\frac{3}{4}+\frac{1}{3}+\frac{2}{3})=\frac{7}{12} macro- R=31∑i=13Ri=31×(43+31+32)=127
macro- F 1 = 1 3 ∑ i = 1 3 F 1 i = 241 420 \text { macro- } \mathrm{F1}=\frac{1}{3} \sum_{i=1}^{3} F 1_{i} =\frac{241}{420} macro- F1=31∑i=13F1i=420241
3、
micro- P = micro- R = micro- F 1 = 3 + 1 + 2 10 = 3 5 \text { micro- } P=\text { micro- } R=\text { micro- } F1=\frac{3+1+2}{10}=\frac{3}{5} micro- P= micro- R= micro- F1=103+1+2=53
🕘 9.5 ROC曲线和AUC
受试者工作特征(Receiver Operating Characteristic,ROC)曲线(curve)和该曲线下面积(Area Under ROC curve,AUC)常作为二分类学习器的性能指标。
🕤 9.5.1 ROC曲线
ROC曲线源于二战中对敌机侦查检测的雷达信号分析技术。根据学习器的预测结果对样例进行排序,按照顺序把样例逐个作为阈值截断点,每次计算出两个值,即真正例率(Ture Positive Rate,TPR)和假正例率(False Positive Rate,FPR),分别以它们为横纵坐标作图,就得到了ROC曲线。
真正例率定义:
T
P
R
=
T
P
T
P
+
F
N
T P R=\frac{T P}{T P+F N}
TPR=TP+FNTP
假正例率定义:
F
P
R
=
F
P
T
N
+
F
P
F P R=\frac{F P}{T N+F P}
FPR=TN+FPFP
🕤 9.5.2 绘制ROC曲线
ROC曲线的绘制过程很简单:给定 m + m^+ m+个正例和 m − m^ - m− 个负例,根据学习器预测结果对样例进行排序,然后把分类阈值设定为最大,即把所有样例预测为负例,此时真正例率和假正例率均为0,在坐标(0,0)处标记一个点。然后,将分类阈值依次设定为每个样例的预测值,即依次将每个样例划分为正例。设前一个标记点坐标为(x,y),当前若为真正例,则对应标记点的坐标为( x , y + 1 m + x,y+\frac{1}{m^+} x,y+m+1);当前若为假正例,则对应标记点的坐标为( x + 1 m − , y x+\frac{1}{m^-},y x+m−1,y),然后用线段连接相邻点即得到ROC曲线。
如下图所示,(a)图给出一个ROC曲线的示意图,对角线对应于“随机猜测”模型。现实任务中通常是利用有限个测试样例来绘制ROC曲线,此时仅能获得有限个坐标对,无法产生光滑的ROC曲线,如(b)图。
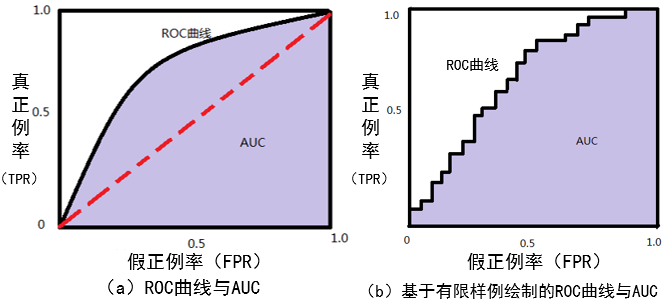
🕤 9.5.3 ROC曲线的意义
还是核酸检测的例子,检测人员的主要任务是尽量把阳性样本判断出来,也就是第一个指标TPR越高越好,而把阴性样本误判为阳性的,也就是第二个指标FPR越低越好。不难发现,这两个指标是相互制约的。如果某次采样是在高风险地区且十人一管,那么它的第一个指标应该会很高,但是第二个指标也相应地变高。最极端的情况下,检测人员把所有的样本都判断为阳性,那么第一个指标达到1,而第二个指标也为1。
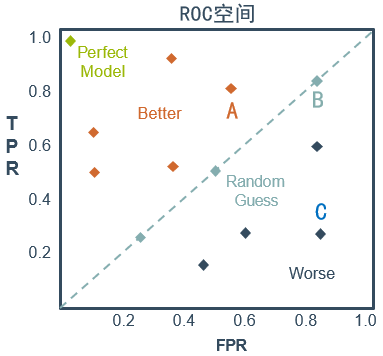
从上图可以看出,左上角的点(TPR=1,FPR=0)为完美分类,也就是这个检测人员手法娴熟,没有出现误操作。点A(TPR>FPR)表明检测人员A的判断大体是正确的。中线上的点B(TPR=FPR)表明检测人员B对一半错一半。下半平面的点C(TPR<FPR)表明检测人员C测的几乎都是“假阳性”,即检测人员C的结果我们要反着看。图中一个阈值得到一个点。现在我们需要一个独立于阈值的评价指标来衡量这个检测人员的水平如何,也就是遍历所有的阈值,得到ROC曲线。
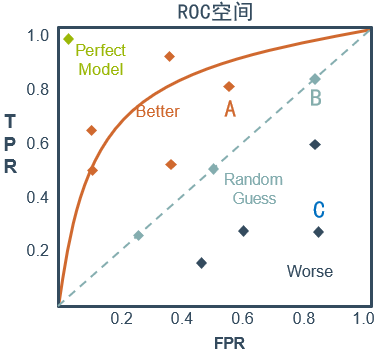
ROC曲线的作用与优点是:
- 能很容易地查出任意阈值对学习器的泛化性能影响。
- 有助于选择最佳的阈值。ROC曲线越靠近左上角,模型的查全率就越高。最靠近左上角的ROC曲线上的点是分类错误最少的阈值,其假正例和假负例总数最少。
- 可以比较不同学习器的性能。将各学习器的ROC曲线绘制在同一坐标中,直观地鉴别优劣,靠近左上角的ROC曲线所代表的学习器准确性最高。
🕤 9.5.4 AUC
进行学习器的比较时,与P-R图相似,若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者;若两个学习器的ROC曲线发生交叉,则难以一般性地断言两者孰优孰劣。此时如果一定要进行比较,则较为合理的判据是比较ROC曲线下的面积,即 AUC
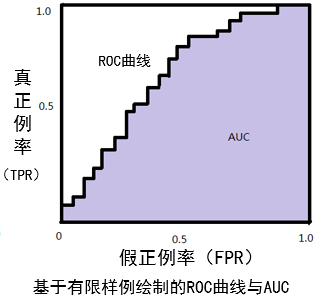
AUC可通过对ROC曲线下各部分的面积求和而得。假定ROC曲线是由坐标的点按序连接而形成(如上图),则AUC可估算为:
A
U
C
=
1
2
∑
i
=
1
m
−
1
(
x
i
+
1
−
x
i
)
(
y
i
+
y
i
+
1
)
A U C=\frac{1}{2} \sum_{i=1}^{m-1}\left(x_{i+1}-x_{i}\right)\left(y_{i}+y_{i+1}\right)
AUC=21i=1∑m−1(xi+1−xi)(yi+yi+1)
AUC的物理意义是:从所有正样本中随机选择一个样本,再从所有负样本中随机选择一个样本,然后用学习器对两个随机样本进行预测,把正样本预测为正例的概率定义为 p 1 p1 p1,把负样本预测为正例的概率定义为 p 2 p2 p2,则 p 1 > p 2 p1>p2 p1>p2的概率就等于 A U C − 1 2 AUC-\frac{1}{2} AUC−21。所以AUC反映的是分类器对样本的排序能力。
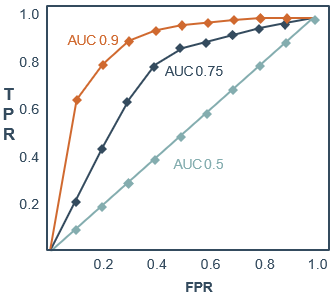
AUC值为ROC曲线所覆盖的区域面积。显然,AUC越大,分类器分类效果越好。
- AUC=1,说明是完美分类器,采用这个模型预测时,不管设定什么阈值都能得出完美预测。绝大多数的预测,不存在完美分类器。
- 0.5<AUC<1,说明优于随机猜测。若这个分类器妥善设定阈值的话,模型具有预测价值。
- AUC=0.5,说明跟随机猜测(例如抛硬币)一样,模型没有预测价值。
- AUC<0.5,说明比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
🕘 9.6 语法
导入想用的评价指标函数:
from sklearn.metrics import accuracy_score
在测试集和预测得到的结果上计算指标值:
accuracy_value = accuracy_score(y_test, y_pred)
其他评价指标函数和检测工具:
from sklearn.metrics import precision_score, recall_score,
f1_score, roc_auc_score,
confusion_matrix, roc_curve,
precision_recall_curve
在线文档:🔎 分类错误评价指标的语法
🕒 10. 综合案例:泰坦尼克号乘客生还预测
泰坦尼克号乘客生还的预测是数据科学竞赛平台Kaggle上最经典的入门竞赛之一。它是一个二分类问题,要求根据乘客的相关信息,如性别、年龄、船舱等级等来预测其是否会生还。
import pandas as pd
# 读入数据
data = pd.read_csv('train.csv') # 假设数据文件存在当前目录下
data.info() # 简单数据分析
<class ‘pandas.core.frame.DataFrame’>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId
\hspace{0.5cm}
891 non-null int64
Survived
\hspace{1cm}
891 non-null int64
Pclass
\hspace{1.3cm}
891 non-null int64
Name
\hspace{1.4cm}
891 non-null object
Sex
\hspace{1.7cm}
891 non-null object
Age
\hspace{1.7cm}
714 non-null float64
SibSp
\hspace{1.5cm}
891 non-null int64
Parch
\hspace{1.5cm}
891 non-null int64
Ticket
\hspace{1.5cm}
891 non-null object
Fare
\hspace{1.7cm}
891 non-null float64
Cabin
\hspace{1.6cm}
204 non-null object
Embarked
\hspace{1cm}
889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB
由此可知,训练集中共有891行和12项。这12项的具体含义如下表所示。
1 PassengerId 乘客编号 2 Survived 是否生还 (1 为生还, 0 为末生还) 3 Pclass 船舱等级 4 Name 乘客姓名 5 Sex 乘客性别 6 Age 乘客年龄 7 SibSp 乘客在船上的兄弟姐妺及配偶数量 8 Parch 乘客在船上的父母和子女数量 9 Ticket 船票编号 10 Fare 票价 11 Cabin 舱位 12 Embarked 登船港口 \begin{array}{|c|c|c|} \hline 1 & \text { PassengerId } & \text { 乘客编号 } \\ \hline 2 & \text { Survived } & \text { 是否生还 (1 为生还, 0 为末生还) } \\ \hline 3 & \text { Pclass } & \text { 船舱等级 } \\ \hline 4 & \text { Name } & \text { 乘客姓名 } \\ \hline 5 & \text { Sex } & \text { 乘客性别 } \\ \hline 6 & \text { Age } & \text { 乘客年龄 } \\ \hline 7 & \text { SibSp } & \text { 乘客在船上的兄弟姐妺及配偶数量 } \\ \hline 8 & \text { Parch } & \text { 乘客在船上的父母和子女数量 } \\ \hline 9 & \text { Ticket } & \text { 船票编号 } \\ \hline 10 & \text { Fare } & \text { 票价 } \\ \hline 11 & \text { Cabin } & \text { 舱位 } \\ \hline 12 & \text { Embarked } & \text { 登船港口 } \\ \hline \end{array} 123456789101112 PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked 乘客编号 是否生还 (1 为生还, 0 为末生还) 船舱等级 乘客姓名 乘客性别 乘客年龄 乘客在船上的兄弟姐妺及配偶数量 乘客在船上的父母和子女数量 船票编号 票价 舱位 登船港口
有些项有缺失值。Age(年龄)有714人有记录,缺失177人的记录;Cabin(舱位)有204人有记录,缺失687人的记录;Embarked(登船港口)有889人有记录,缺失2人的记录。
还可以用下列语句进行数据的描述统计分析:
data.describe()
Passengerld Survived Pclass Age SibSp Parch Fare count 891.000000 891.000000 891.000000 714.000000 891.000000 891.000000 891.000000 mean 446.000000 0.383838 2.308642 29.699118 0.523008 0.381594 32.204208 std 257.353842 0.486592 0.836071 14.526497 1.102743 0.806057 49.693429 min 1.000000 0.000000 1.000000 0.420000 0.000000 0.000000 0.000000 25 % 223.500000 0.000000 2.000000 20.125000 0.000000 0.000000 7.910400 50 % 446.000000 0.000000 3.000000 28.000000 0.000000 0.000000 14.454200 75 % 668.500000 1.000000 3.000000 38.000000 1.000000 0.000000 31.000000 max 891.000000 1.000000 3.000000 80.000000 8.000000 6.000000 512.329200 \begin{array}{rrrrrrrr} & \text { Passengerld } & \text { Survived } & \text { Pclass } & \text { Age } & \text { SibSp } & \text { Parch } & \text { Fare } \\ \hline \text { count } & 891.000000 & 891.000000 & 891.000000 & 714.000000 & 891.000000 & 891.000000 & 891.000000 \\ \text { mean } & 446.000000 & 0.383838 & 2.308642 & 29.699118 & 0.523008 & 0.381594 & 32.204208 \\ \text { std } & 257.353842 & 0.486592 & 0.836071 & 14.526497 & 1.102743 & 0.806057 & 49.693429 \\ \text { min } & 1.000000 & 0.000000 & 1.000000 & 0.420000 & 0.000000 & 0.000000 & 0.000000 \\ \text{25 \%} & 223.500000 & 0.000000 & 2.000000 & 20.125000 & 0.000000 & 0.000000 & 7.910400 \\ \text{50 \%} & 446.000000 & 0.000000 & 3.000000 & 28.000000 & 0.000000 & 0.000000 & 14.454200 \\ \text{75 \%} & 668.500000 & 1.000000 & 3.000000 & 38.000000 & 1.000000 & 0.000000 & 31.000000 \\ \text { max } & 891.000000 & 1.000000 & 3.000000 & 80.000000 & 8.000000 & 6.000000 & 512.329200 \end{array} count mean std min 25 %50 %75 % max Passengerld 891.000000446.000000257.3538421.000000223.500000446.000000668.500000891.000000 Survived 891.0000000.3838380.4865920.0000000.0000000.0000001.0000001.000000 Pclass 891.0000002.3086420.8360711.0000002.0000003.0000003.0000003.000000 Age 714.00000029.69911814.5264970.42000020.12500028.00000038.00000080.000000 SibSp 891.0000000.5230081.1027430.0000000.0000000.0000001.0000008.000000 Parch 891.0000000.3815940.8060570.0000000.0000000.0000000.0000006.000000 Fare 891.00000032.20420849.6934290.0000007.91040014.45420031.000000512.329200
可以看到,乘客的平均年龄为29.7,最大年龄为80.0,最小年龄为0.42。生还人数大约为总体的38%,票价最贵的为512.33美元等。
各属性与生还情况的关联。此数据集有10个属性,我们主要拿出性别和登船港口两个属性分析生还率,其余属性分析类似。
(1)不同性别的生还情况
import matplotlib.pyplot as plt
%matplotlib inline
Survived_m = data.Survived[data.Sex == 'male'].value_counts()
Survived_f = data.Survived[data.Sex == 'female'].value_counts()
df = pd.DataFrame({u'男性':Survived_m, u'女性':Survived_f})
df.plot(kind = 'bar', stacked = True)
plt.title(u'按性别看获救情况')
plt.xlabel(u'获救')
plt.ylabel(u'人数')
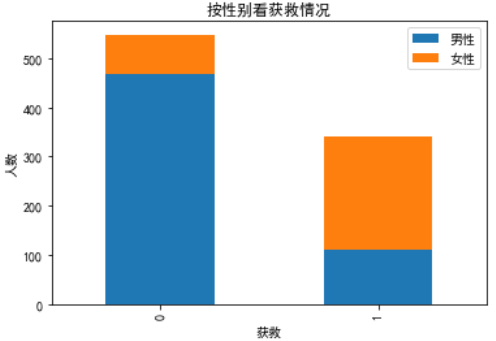
0代表未生还,1代表生还。明显可以看出,未生还人员中男性乘客比例较大,而生还人员中女性乘客比例较大。所以很大程度上可以确定性别是预测生还情况的一个重要因素。
(2)不同登船港口乘客的生还情况
Survived_0 = data_train.Embarked[data_train.Survived == 0].value_counts()
Survived_1 = data_train.Embarked[data_train.Survived == 1].value_counts()
df = pd.DataFrame({u'获救':Survived_1,u'未获救':Survived_0})
df.plot(kind = 'bar', stacked = True)
plt.title(u'各登船港口乘客的获救情况')
plt.xlabel(u'登船港口')
plt.ylabel(u'人数')
plt.show()
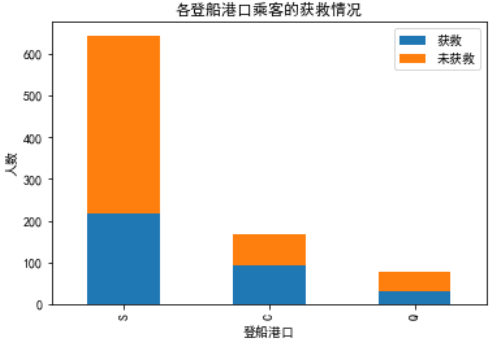
我们把生还人数占各个港口登船总人数的比例看成分析条件,总的来说C港口的生还率高一些,S港口的生还率相对低一些。
数据预处理。数据预处理包括无关特征的删除、填充缺失值、编码转换、数据缩放等。
# 删除姓名、ID、船票、客舱等无关信息,axis=0 删除行,=1 删除列
data.drop(['Name','PassengerId','Ticket','Cabin'], axis=1, inplace=True)
# 用平均值或众数填充缺失数据
data['Age'] = data['Age'].fillna(data['Age'].mean())
data['Fare'] = data['Fare'].fillna(data['Fare'].mean())
data['Embarked'] = data['Embarked'].fillna(data['Embarked'].value_counts().index[0])
# 将性别与登船港口进行独热编码(即独一性,比如一个人在一个港口登船,就不可能在另一个港口登船)
dumm = pd.get_dummies(data[['Sex','Embarked']], drop_first=True)
data = pd.concat([data, dumm], axis=1)
data.drop(['Sex','Embarked'], axis=1, inplace=True)
# 数据缩放
data['Age']=(data['Age']-data['Age'].min())/(data['Age'].max()-data['Age'].min())
data['Fare']=(data['Fare']-data['Fare'].min())/( data['Fare'].max()-data['Fare'].min())
from sklearn.model_selection import train_test_split
# 划分训练集和测试集,即预留一部分数据(30%),用于评价模型
X = data.drop('Survived', axis=1)
y = data.Survived
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression() # 创建模型
LR.fit(X_train, y_train) # 训练模型
print('训练集准确率:\n', LR.score(X_train, y_train))
print('验证集准确率:\n', LR.score(X_test, y_test))
训练集准确率: 0.7897271268057785
验证集准确率: 0.832089552238806
可以看到,该模型在测试集上的准确率高于训练集上的准确率,没有过拟合,可以考虑增加模型参数或复杂度。逻辑回归模型关于泰坦尼克号乘客生还能达到较好的预测效果。
y_pred = LR.predict(X_test) # 预测测试数据
from sklearn import metrics
# 绘制混淆矩阵
print(metrics.confusion_matrix(y_test, y_pred))
[ [ 150 25 ] [ 31 62 ] ] \ [ \ [ \ 150 \quad 25 \ ] \\ \quad [ \ 31 \quad 62 \ ] \ ] [ [ 15025 ][ 3162 ] ]
上面混淆矩阵的含义如下所示:
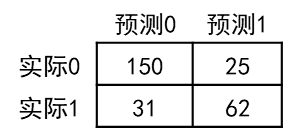
我们可以看到真正例的个数是62,真负例的个数是150。
由混淆矩阵可以计算得出许多评价指标,如下所示。
print(metrics.precision_score(y_test, y_pred))
print(metrics.recall_score(y_test, y_pred))
print(metrics.f1_score(y_test, y_pred))
print(metrics.accuracy_score(y_test, y_pred))
0.7126436781609196 0.6666666666666666 0.6888888888888889 0.7910447761194029 0.7126436781609196 \\ 0.6666666666666666 \\ 0.6888888888888889 \\ 0.7910447761194029 0.71264367816091960.66666666666666660.68888888888888890.7910447761194029
当然,还可以使用分类报告的形式显示出所有类别的查准率、查全率和F1分数等。
print(metrics.classification_report(y_test, y_pred))
precision recall f1-score support 0 0.83 0.86 0.84 175 1 0.71 0.67 0.69 93 micro avg 0.79 0.79 0.79 268 macro avg 0.77 0.76 0.77 268 weighted avg 0.79 0.79 0.79 268 \hspace{2cm}\text{precision \qquad recall \qquad f1-score \qquad support} \\ {} \\ \hspace{1cm}0 \hspace{1.2cm} 0.83 \hspace{1.2cm} 0.86 \hspace{1.2cm} 0.84 \hspace{1.3cm} 175 \\ \hspace{1cm}1 \hspace{1.2cm} 0.71 \hspace{1.2cm} 0.67 \hspace{1.2cm} 0.69 \hspace{1.4cm} 93 \\ {} \\ \hspace{0.2cm}\text{micro \ avg} \hspace{0.6cm} 0.79 \hspace{1.2cm} 0.79 \hspace{1.2cm} 0.79 \hspace{1.3cm} 268 \\ \hspace{0.2cm}\text{macro \ avg} \hspace{0.55cm} 0.77 \hspace{1.2cm} 0.76 \hspace{1.2cm} 0.77 \hspace{1.3cm} 268 \\ \hspace{0.1cm} \text{weighted \ avg} \hspace{0.24cm} 0.79 \hspace{1.2cm} 0.79 \hspace{1.2cm} 0.79 \hspace{1.3cm} 268 precision recall f1-score support00.830.860.8417510.710.670.6993micro avg0.790.790.79268macro avg0.770.760.77268weighted avg0.790.790.79268
绘制ROC曲线,并计算AUC。
绘制ROC曲线需要分类器输出预测每个样例属于正类的概率值。
y_pred_prob = LR.predict_proba(X_test)
# 计算ROC曲线,即真正例率、假正例率、分类阈值等。
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pred_prob[:,1])
print(metrics.auc(fpr, tpr)) # 计算AUC值
0.8227342549923196 0.8227342549923196 0.8227342549923196
绘制ROC曲线
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(fpr, tpr, lw=2, label='ROC curve (area={:.2f})'.format(auc))
plt.plot([0,1],[0,1],'r--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc='lower right')
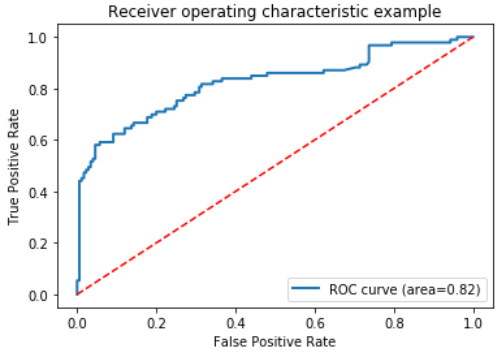
参考文献:🔎 利用Python分析泰坦尼克号数据集
🕒 12. 课后习题
-
【单选题】假设模型响应 y y y与输入特征 x x x(特征个数为n-1)之间满足线性关系 y = f ( x , ω ) = ω T x y=f(x,\omega)=\omega^Tx y=f(x,ω)=ωTx ,现有训练数据 ( X , y ) (X,y) (X,y),其中 X X X为输入样本(总数为m)的特征矩阵, y y y为m个样本的标签(响应)向量,则其岭回归模型的目标函数 J ( ω ) J(\omega) J(ω)为( )
A. J ( ω ) = ( X ω − y ) T ( X ω − y ) J(\omega)=(X \omega-y)^{T}(X \omega-y) J(ω)=(Xω−y)T(Xω−y)
B. J ( ω ) = ( X ω − y ) T ( X ω − y ) + α ∑ i = 1 n ω i 2 J(\omega)=(X \omega-y)^{T}(X \omega-y)+\alpha \sum_{i=1}^{n} \omega_{i}^{2} J(ω)=(Xω−y)T(Xω−y)+α∑i=1nωi2,其中 α \alpha α为正则系数, ω i \omega_i ωi为第 i i i个特征系数
C. J ( ω ) = ∑ i = 1 m ∣ x i ω − y i ∣ + α ∑ i = 1 n ∣ ω i ∣ J(\omega)=\sum_{i=1}^{m}\left|x_{i} \omega-y_{i}\right|+\alpha \sum_{i=1}^{n}\left|\omega_{i}\right| J(ω)=∑i=1m∣xiω−yi∣+α∑i=1n∣ωi∣,其中 α \alpha α为正则系数, ω i \omega_i ωi为第 i i i个特征系数, x i x_i xi为第 i i i个样本的特征向量, y i y_i yi为第 i i i个样本的标签
D. J ( ω ) = ( X w − y ) T ( X w − y ) + α ∑ i = 1 n ∣ ω i ∣ J(\omega)=(X w-y)^{T}(X w-y)+\alpha \sum_{i=1}^{n}\left|\omega_{i}\right| J(ω)=(Xw−y)T(Xw−y)+α∑i=1n∣ωi∣,其中 α \alpha α为正则系数, ω i \omega_i ωi为第 i i i个特征系数 -
【单选题】在解决某二分类问题前,对训练样本数据(含特征x1,x2)集分析,发现其样本分布如下:
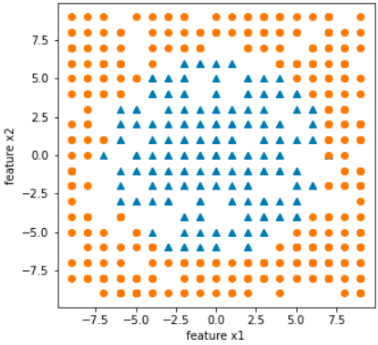
如使用逻辑回归解决该分类问题,选择训练模型的函数形式为( )的逻辑回归模型比较合适。
A. f ( x ) = 1 1 + e − ( ω 0 + ω 1 x 1 + ω 2 x 2 ) f(x)=\frac{1}{1+e^{-(\omega_0+\omega_1x_1+\omega_2x_2)}} f(x)=1+e−(ω0+ω1x1+ω2x2)1
B. f ( x ) = 1 1 + e − ( ω 0 + ω 1 x 1 + ω 1 2 x 2 2 ) f(x)=\frac{1}{1+e^{-(\omega_0+\omega_1x_1+\omega^2_1x^2_2)}} f(x)=1+e−(ω0+ω1x1+ω12x22)1
C. f ( x ) = 1 1 + e − ( ω 0 + ω 1 x 1 + ω 2 x 2 + ω 3 x 1 x 2 ) f(x)=\frac{1}{1+e^{-(\omega_0+\omega_1x_1+\omega_2x_2+\omega_3x_1x_2)}} f(x)=1+e−(ω0+ω1x1+ω2x2+ω3x1x2)1
D. f ( x ) = 1 1 + e − ( ω 0 + ω 1 x 1 + ω 2 x 2 + ω 3 x 1 2 + ω 4 x 2 2 ) f(x)=\frac{1}{1+e^{-(\omega_0+\omega_1x_1+\omega_2x_2+\omega_3x^2_1+\omega_4x^2_2)}} f(x)=1+e−(ω0+ω1x1+ω2x2+ω3x12+ω4x22)1 -
【单选题】关于在正则化线性回归模型的说法,以下错误的是( )
A. 使用L1正则化的线性回归模型称为套索回归,套索回归易于产生稀疏模型,可用于特征选择。
B. 套索回归的目标函数连续可导,所以可用解析法求解最优模型参数。
C. 相比不含正则项的线性回归模型,正则化之后的线性回归模型过拟合的可能性变小。
D. 使用L2正则化的线性回归模型称为岭回归,岭回归倾向于生成参数较小,但不为0的模型。 -
【单选题】在鸢尾花分类示例中,鸢尾花有三种可能的类别,如采用一对其余策略用逻辑回归解决该分类问题,则需要训练( )个模型。
A. 1
B. 2
C. 3
D. 4 -
【单选题】一般认为,线性回归问题中的残差满足标准正态分布的假设是合理的。因此,关于线性回归问题中的残差,下列说法( )是正确的。
A. 残差的平均值总是零
B. 残差的平均值总是小于零
C. 残差的平均值总是大于零
D. 对于残差没有限制 -
【单选题】在线性回归的目标函数中添加正则项,其对预测模型带来的可能积极后果中不包括( )
A. 有利于防止过拟合,提高模型泛化能力
B. 削弱不重要特征,自动提取重要特征,有利于特征选择
C. 有利于提高模型拟合程度,减少模型训练误差
D. 有利于缩小特征对应的参数值,避免出现过大参数 -
【单选题】如果套索回归的正则参数很大,则训练所得的( )
A. 预测模型的一些系数大几率将变为0
B. 预测模型的一些系数将接近0,但不是绝对等于0
C. 预测模型的个别系数将变得很大,远超1
D. 预测模型的所有系数都将变得很大,远超1 -
【单选题】已收集到一组房屋的房价数据,每个房屋数据包括该房屋的特征和房价(面积,房间数量,楼层,房龄,房价)值,记作。假设房屋特征和房价满足线性关系,依据该组数据建立预测房价的线性回归模型的函数形式为( )
A. y = ω 0 + ω 1 x 1 + ω 2 x 2 + ω 3 x 3 + ω 4 x 4 y=\omega_{0}+\omega_{1} x_{1}+\omega_{2} x_{2}+\omega_{3} x_{3}+\omega_{4} x_{4} y=ω0+ω1x1+ω2x2+ω3x3+ω4x4
B. y = ω 1 x 1 + ω 2 x 2 + ω 3 x 3 + ω 4 x 4 y=\omega_{1} x_{1}+\omega_{2} x_{2}+\omega_{3} x_{3}+\omega_{4} x_{4} y=ω1x1+ω2x2+ω3x3+ω4x4
C. y = ω ( x 1 + x 2 + x 3 + x 4 ) + b y=\omega\left(x_{1}+x_{2}+x_{3}+x_{4}\right)+b y=ω(x1+x2+x3+x4)+b
D. y = ω x 1 x 2 x 3 x 4 + b y=\omega x_{1} x_{2} x_{3} x_{4}+b y=ωx1x2x3x4+b -
【判断题】逻辑回归模型的超参数调优可以采用交叉验证方式,交叉验证时数据集划分为训练集、测试集和验证集,取不同超参数的模型可通过其验证集上的性能进行评价和比较优劣。
-
【判断题】 岭回归目标函数中的正规项系数调优可以在岭回归模型的参数优化求解过程中实现。
-
【单选题】以下关于二分类学习器性能指标ROC的说法,错误的是( )
A. ROC曲线可直观反映学习器在不同分类阈值下的真正例率和假正例率的关系,适用于综合评价模型准确性。
B. 测试集中正负样本的分布发生变化时,ROC曲线形状会发生较大变化。
C. ROC曲线上最靠近左上角的点的阈值,是模型分类错误最少的最佳分类阈值。
D. 将不同学习器ROC曲线绘制在同一坐标中,直观上,“拱起”程度越高,越靠近左上角的ROC曲线代表的学习器准确性越高。 -
【单选题】以下关于二分类学习器性能指标AUC的说法,错误的是( )
A. AUC值为ROC曲线覆盖的区域面积。
B. 0.5<AUC<1,分类器总体(考虑不同分类阈值)准确性优于随机猜测,选择合理阈值,模型具有预测价值。
C. AUC=0.5,分类器总体(考虑不同分类阈值)准确性与随机猜测相当,模型没有预测价值。
D. 如果将贝利和章鱼保罗视作足球结果预测的二分类模型,则贝利的AUC值大于章鱼保罗的AUC值。
答案:1.B 2.D 3.B 4.C 5.A 6.C 7.A 8.A 9.√ 10.× 11.B 12.D
这篇文章爆肝了整整三天,做的贼累,求个三连不过分吧~
OK,以上就是本期知识点“线性回归、逻辑回归与分类评价指标”的知识啦~~ ,感谢友友们的阅读。后续还会继续更新,欢迎持续关注哟📌~
💫如果有错误❌,欢迎批评指正呀👀~让我们一起相互进步🚀
🎉如果觉得收获满满,可以点点赞👍支持一下哟~
❗ 转载请注明出处
作者:HinsCoder
博客链接:🔎 作者博客主页