目录链接:
力扣编程题-解法汇总_分享+记录-CSDN博客
GitHub同步刷题项目:
https://github.com/September26/java-algorithms
原题链接:力扣
描述:
给定一个有 N 个结点的二叉树的根结点 root,树中的每个结点上都对应有 node.val 枚硬币,并且总共有 N 枚硬币。
在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点,或者从子结点移动到父结点。)。
返回使每个结点上只有一枚硬币所需的移动次数。
示例 1:
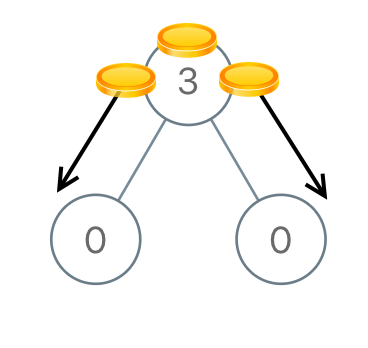
输入:[3,0,0] 输出:2 解释:从树的根结点开始,我们将一枚硬币移到它的左子结点上,一枚硬币移到它的右子结点上。
示例 2:
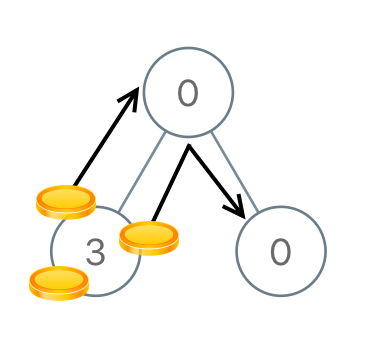
输入:[0,3,0] 输出:3 解释:从根结点的左子结点开始,我们将两枚硬币移到根结点上 [移动两次]。然后,我们把一枚硬币从根结点移到右子结点上。
示例 3:
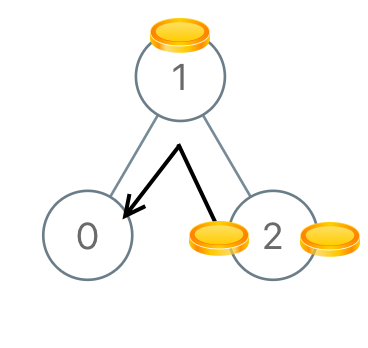
输入:[1,0,2] 输出:2
示例 4:
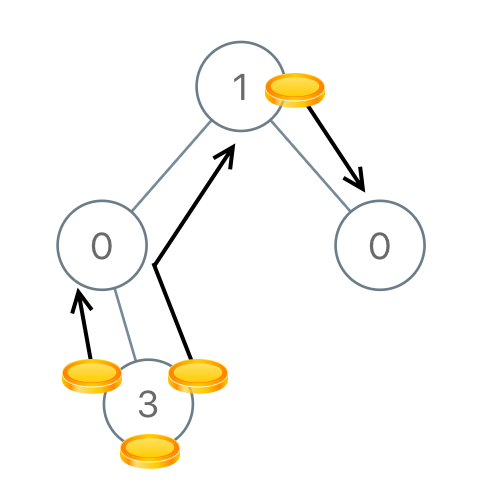
输入:[1,0,0,null,3] 输出:4
提示:
1<= N <= 1000 <= node.val <= N
解题思路:
* 解题思路:
* 其实这道题和平衡二叉树很像。
* 我们构建两颗树,
* 第一颗树numMap,记录每个节点及其子节点应该有多少个硬币。
* 第二颗树sumMap,记录每个节点及其子节点当前有多少个硬币。
* 每个节点当前具有的,减去应该具有的硬币数量,其差值的绝对值就是每个节点应该送出或者接受的数量。
* 求这个差值的和就是我们想要的结果。
代码:
class Solution979
{
public:
int getTreeNodeNum(TreeNode *node, std::map<TreeNode *, int> &numMap)
{
if (node == nullptr)
{
return 0;
}
int num = 1;
num += getTreeNodeNum(node->left, numMap);
num += getTreeNodeNum(node->right, numMap);
numMap[node] = num;
return num;
}
int getTreeNodeSum(TreeNode *node, std::map<TreeNode *, int> &sumMap)
{
if (node == nullptr)
{
return 0;
}
int sum = node->val;
sum += getTreeNodeSum(node->left, sumMap);
sum += getTreeNodeSum(node->right, sumMap);
sumMap[node] = sum;
return sum;
}
int distributeCoins(TreeNode *root)
{
int sum = 0;
std::map<TreeNode *, int> numMap;
std::map<TreeNode *, int> sumMap;
getTreeNodeNum(root, numMap);
getTreeNodeSum(root, sumMap);
// std::cout << "Value: " << sumMap.size() << std::endl;
int result = 0;
for (auto it = numMap.begin(); it != numMap.end(); ++it)
{
int sum = sumMap[it->first];
int num = it->second;
result += abs(sum - num);
}
return result;
}
};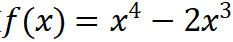






![[GFCTF 2021]Baby_Web(CVE-2021-41773) 从一道题入门PHP代码审计 (保姆级)](https://img-blog.csdnimg.cn/img_convert/48352596c40573e5568ab1a53f8be7e6.png)