257.二叉树的所有路径

题目

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

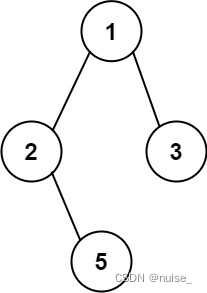
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

• 树中节点的数目在范围 [1, 100] 内
• -100 <= Node.val <= 100

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/binary-tree-paths
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

这道题的内核还是遍历一棵二叉树，返回值是由一条一条路径组成的数组。

什么时候将路径返回？也就是递归的终止条件是什么？
当遍历到叶子节点时，说明这条路径已经遍历结束，可以将路径存放进结果集中。
每一次递归都是往下走一步，递归的返回相当于回溯到了上一个状态

递归的参数和返回值是什么
由上一个问题我们知道，遇见叶子节点需要将路径放入结果集。路径存放在哪里？随着每一次递归的向下走，都需要将当前的节点值放入路径中，所以要么路径是全局的遍历，要么路径作为函数的参数传递上一次的路径信息。同样的道理，结果集也可以是函数的参数，也可以是全局变量。
我设置的参数有以下三个，递归函数的返回值当然就是最终的结果集res了。
1.当前指向的节点root
2.存放当前路径的字符串path
3.存放结果集的数组res

var binaryTreePaths = function(root,path="",res=[]);

本层递归的逻辑
每一层递归需要做的事情就是将当前的root节点值加入路径中，然后将其左孩子节点加入路径中，最后将其右孩子节点加入路径中。
所以递归函数的作用可以抽象为将root节点加入path路径中，这里需要注意的点是递归返回的时候是会回到上一个状态，path记录从根节点到当前节点root的路径，所以此时路径同样需要回溯到上一个状态。

开始我们打算将path定义为字符串，这里分析发现后还需要回溯，而结果中"1->2->5"并不方便回溯操作。于是我们把path定义为数组，最后遍历到叶子节点加入结果集res时，才将其转换为字符串。

var binaryTreePaths = function(root,path=[],res=[]) {
    if(root.right==null && root.left==null){
    //当前root为叶子节点
    path.push(root.val);
    res.push(path.join("->"));
    return res;
    }
    path.push(root.val);
    if(root.left!=null){
        binaryTreePaths(root.left,path,res);//这里的递归结束后会回到了本次递归的状态，所以被这个递归函数改变的path值也需要复原。
        path.pop();//回溯
    }
    if(root.right!=null){
        binaryTreePaths(root.right,path,res);
        path.pop(); //回溯
    }
    
    return res;
};

知识点:递归和回溯永远在一起，递归之中隐含了回溯。

技巧 - 参数的作用域

之前的方法中我们传递的path参数是数组的地址，所以后面的递归函数也可以修改本次递归的path值。
如果我们将path设置为字符串，参数传递时传递拷贝的值，那么后面的递归函数并没有修改本次递归中的path值，也实现了回溯的思想。
如下例，参数传递的是path+"->",是值传递，那么内层的递归是不会影响本次的path值。

//本次递归的代码，假设本层的path=A
    if(root.left!=null){
        binaryTreePaths(root.left,path+"->",res);//binaryTreePaths调用之后的path值A-> 的内层递归
       //回到本次递归后，path=A 并没有被修改，相当于回溯了 
    }
    if(root.right!=null){
        binaryTreePaths(root.right,path+"->",res);
    }

完整代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {string[]}
 */
var binaryTreePaths = function(root,path="",res=[]) {
    if(root.right==null && root.left==null){
    //当前root为叶子节点
    path+=root.val;
    res.push(path);
    return res;
    }
    path+=root.val;
    if(root.left!=null){
        binaryTreePaths(root.left,path+"->",res);
    }
    if(root.right!=null){
        binaryTreePaths(root.right,path+"->",res);
    }
    
    return res;
};

巧妙的题解方法

题解里面的递归解法很巧妙，我只想到了深度优先搜索和广度优先搜索。

这里记录下递归解法
如果我知道了左子树和右子树的所有路径，我们在用根节点和他们连在一起，就得到了从根节点到所有叶子节点的所有路径。

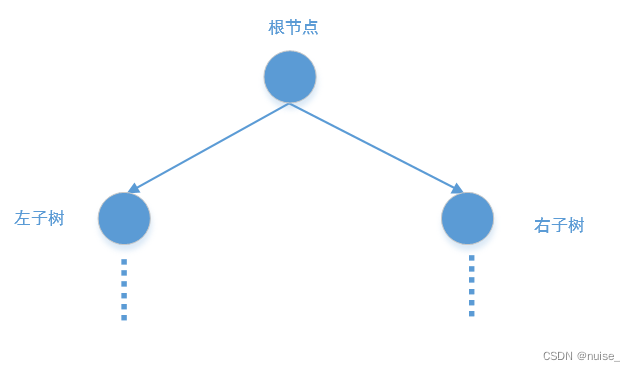
binaryTreePaths=function(root){}函数抽象返回从叶子节点到root节点的路径。

var binaryTreePaths = function(root) {
    const res = new Array();
        if (root == null)
            return res;
        //到达叶子节点，把路径加入到集合中
        if (root.left == null && root.right == null) {
            res.push(root.val+"");
            return res;
        }
        //遍历左子节点的路径,在路径在最前方添加上当前节点
        for (let path of binaryTreePaths(root.left)) {
            res.push(root.val + "->" + path);
        }
        //遍历右子节点的路径.在路径在最前方添加上当前节点
        for (let path of binaryTreePaths(root.right)) {
            res.push(root.val + "->" + path);
        }
        return res;
};`

作者：sdwwld
链接：https://leetcode.cn/problems/binary-tree-paths/solution/257-er-cha-shu-de-suo-you-lu-jing-tu-wen-jie-xi-by/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。