💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
文献来源1:

电池单元总容量是指可以从充满电的电池中提取的电荷总量。了解当前总容量值对于能够计算电池组的最大储能能力、电池组中的剩余能量以及作为电池健康状况的指标非常重要。我们表明,估计电池单元总容量的传统方法(仅在累积安培小时测量中考虑噪声)是有偏差的。电池单元总容量的估算必须同时了解充电状态估计值的噪声和用于计算总容量估计值的累积安培小时测量值。我们演示了总最小二乘法如何比传统方法提供更好的结果,并推导出适合在嵌入式电池管理系统中实现的近似加权总最小二乘算法。
原文摘要:
Abstract
Battery cell total capacity refers to the total amount of charge that can be extracted from a fully charged cell. Knowledge of the present total capacity value is important to being able to calculate the maximum energy storage capability of a battery pack, the remaining energy in a battery pack, and as an indicator of the battery’s state of health. We show that traditional methods of estimating battery cell total capacity, which consider noises only in the accumulated ampere hour measurement, are biased. Battery cell total capacity must be estimated with knowledge of both the noises on the state of charge estimates and on the accumulated ampere hour measurements used to compute the total capacity estimate. We demonstrate how total least squares gives better results than traditional methods, and derive an approximate weighted total least squares algorithm that is suitable for implementation in an embedded battery management system.
文献来源2:

近年来,锂电池在电力和耗能应用中的使用急剧增加。对于此类应用,有必要将电池串联和并联的大型电池组件中。由于大量细胞一起运作,有必要了解它们的内在变异性,不仅在初始阶段,而且在衰老时。在这项研究中,我们研究了一批商业细胞,以解决它们最初的细胞间变异以及循环引起的变异。为此,我们不仅跟踪了与电池性能、最大容量、电阻和倍率能力相关的几个指标,还通过非侵入性量化锂库存损失(LLI)、活性材料损失(LAM)和两个电极上的动力学降解来跟踪降解机制。我们发现,即使初始细胞间差异很小,衰老时也会观察到显着的变化,因为细胞以不同的速度降解。我们还观察到这些变异与初始变异无关。
原文摘要:
Abstract
The use of lithium batteries for power and energy-hungry applications has risen drastically in recent years. For such applications, it is necessary to connect the batteries in large assemblies of cells in series and parallel. With a large number of cells operating together, it is necessary to understand their intrinsic variabilities, not only at the initial stage but also upon aging. In this study, we studied a batch of commercial cells to address their initial cell-to-cell variations and also the variations induced by cycling. To do so, we not only tracked several metrics associated with cell performance, the maximum capacity, the resistance, and the rate capability but also the degradation mechanism via a non-invasive quantification of the loss of lithium inventory (LLI), the loss of active material (LAM) and the kinetic degradation on both electrodes. We found that, even with small initial cell-to-cell variations, significant variations will be observed upon aging because the cells degrade at a different pace. We also observed that these variations were not correlated with the initial variations.
Keywords:
lithium-ion battery degradation; intrinsic variability; cell screening; cell-to-cell variations
锂离子电池在当今世界有许多应用。锂离子电池的一些主要市场包括手机、笔记本电脑(PC)、电动汽车[1]和电网存储[2]。在高输出电压应用中,通常将许多锂离子电池串联组装以满足系统要求。对于笔记本电脑,通常需要两到四个电池串;而在车辆应用中,这个数字可能高达100。电网存储可能需要更大系列的单元。电池组设计中这种方便的可扩展性也有一些缺点。其中之一是,一串锂离子电池的耐用性只能与其最弱的组件一样耐用。这个公理在短期(例如,容量)和长期(例如,退化)考虑方面都是正确的。因此,为了优化电池组的性能,需要匹配构成电池组的电池的内在特性。关于短期考虑,阻抗和容量匹配可以在装配线末端、工厂或在其设施内交付给客户时实现。长期考虑因素的管理更具挑战性。最大限度地延长电池组的使用寿命要求其所有电池以几乎相同的方式降解,因此没有薄弱环节。迄今为止,衰老时细胞之间的差异已被证明存在[3,4,5,6],并且很难(如果不是不可能的话)及时和资源节约的方式预测数百万个细胞的循环寿命。
这是一个问题,因为内在退化变异性太大或尚未量化有几个含义。对于电池设计人员来说,很难比较竞争的电池设计并确定卓越的设计。对于电池集成商来说,它在充电平衡策略[7]和保修条款方面提出了严峻的挑战。对于学术研究人员和潜在的工业买家来说,它质疑在耐久性研究中是否可以得出合理的结论,几乎没有重复性。对于电池供电设备的客户来说,如果电池过早磨损,可能会导致使用损失和经济困难。
关于量化接收到的细胞间变化的最新技术的讨论超出了本文的范围。对于这样的讨论,读者可以参考Rumpf等人的文章[8]。一批细胞内初始细胞间变异的程度虽然报道不够频繁,但一直是文献中多项研究的主题[4,5,6,8,9,10,11,12,13]。研究人员报告了对12个[14],50个[5,15,16],100个[17,18,19,20]和1000个[8,9,10,21]细胞的统计研究。所有这些研究都确定批次中的细胞是不同的,需要量化和考虑这些差异。这些研究侧重于电池之间容量和电阻的变化,但没有解决电极平衡的变化。最近对此问题进行了研究,并报告了基于低速率循环数据的批次51个细胞的电极匹配的细胞间变化[22]。以前的文献表明,这些初始变化可以被表征并因此量化。为了适应这种内在退化特征的扩散,可以实施一些缓解策略。
很少有研究关注长期考虑[3,4,5,6]。在这些研究中,报告了循环寿命的明显分布。这些研究的结论支持这样的假设,即尽管在生命开始时(BOL)的细胞间差异很小,但这些细胞的周期老化和日历老化存在内在变异性。然而,这些研究未能确定观察到的降解扩散的实际起源。为了能够更好地进行背面耐久性建模[23,24],进一步检查商用电池中退化扩散的实际程度至关重要。在这项研究中,锂离子18650格式电池非常适合,因为它们的批量生产非常大,由于这些商品的普遍存在而导致生产过程的相对成熟度,以及它们在当前电动汽车电池组中的使用[25]。
本研究的目的是阐明一组常用来源的锂离子电池是否会在循环老化过程中经历其降解行为的显着变化。这个问题有两个方面:首先,所有细胞是否都以相同的速度降解;其次,所有的细胞都是以同样的方式降解的吗?为了回答这个问题,在相同条件下将细胞循环1000次,并在容量和电阻的基础上进行分析,但也通过非侵入性电化学电压谱进行分析[26,27]。

📚2 运行结果

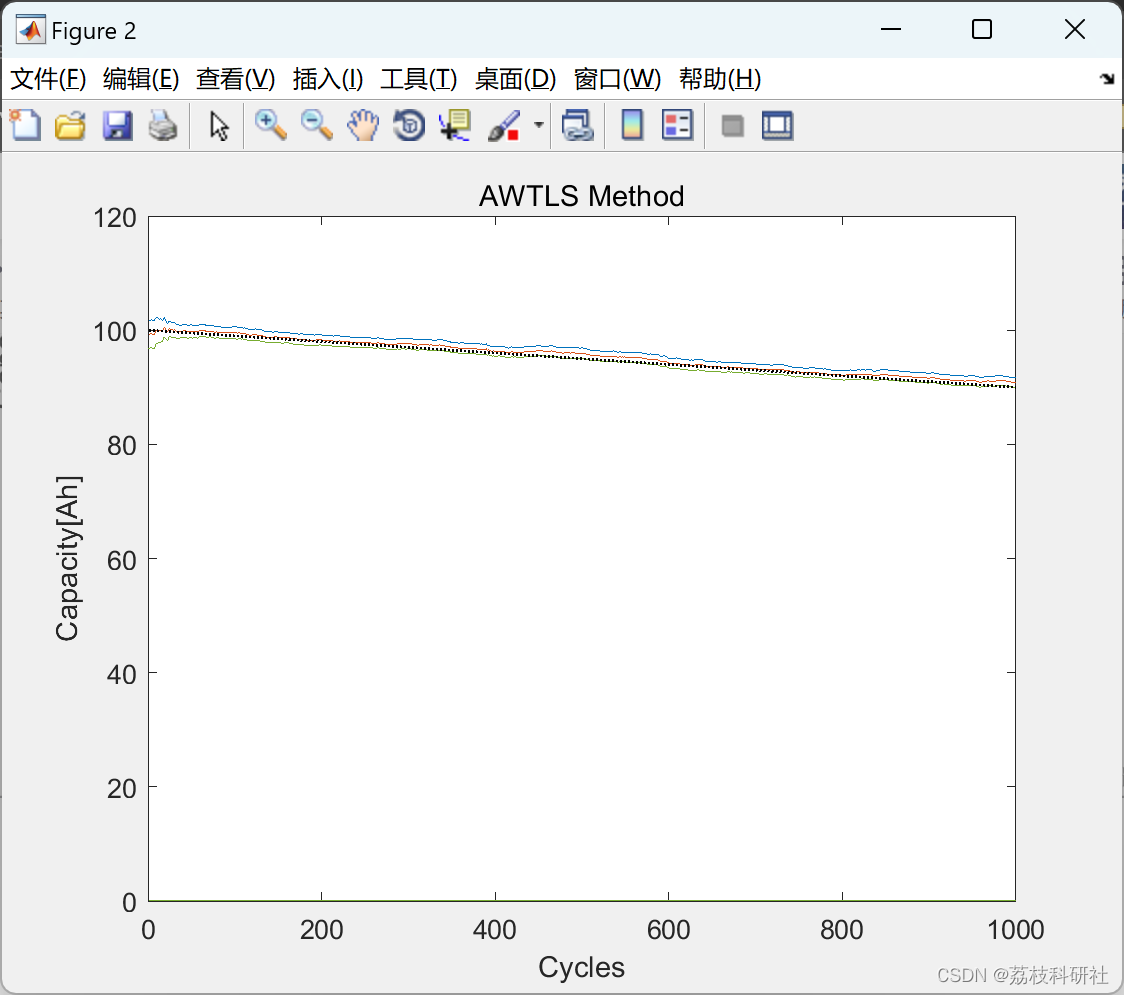
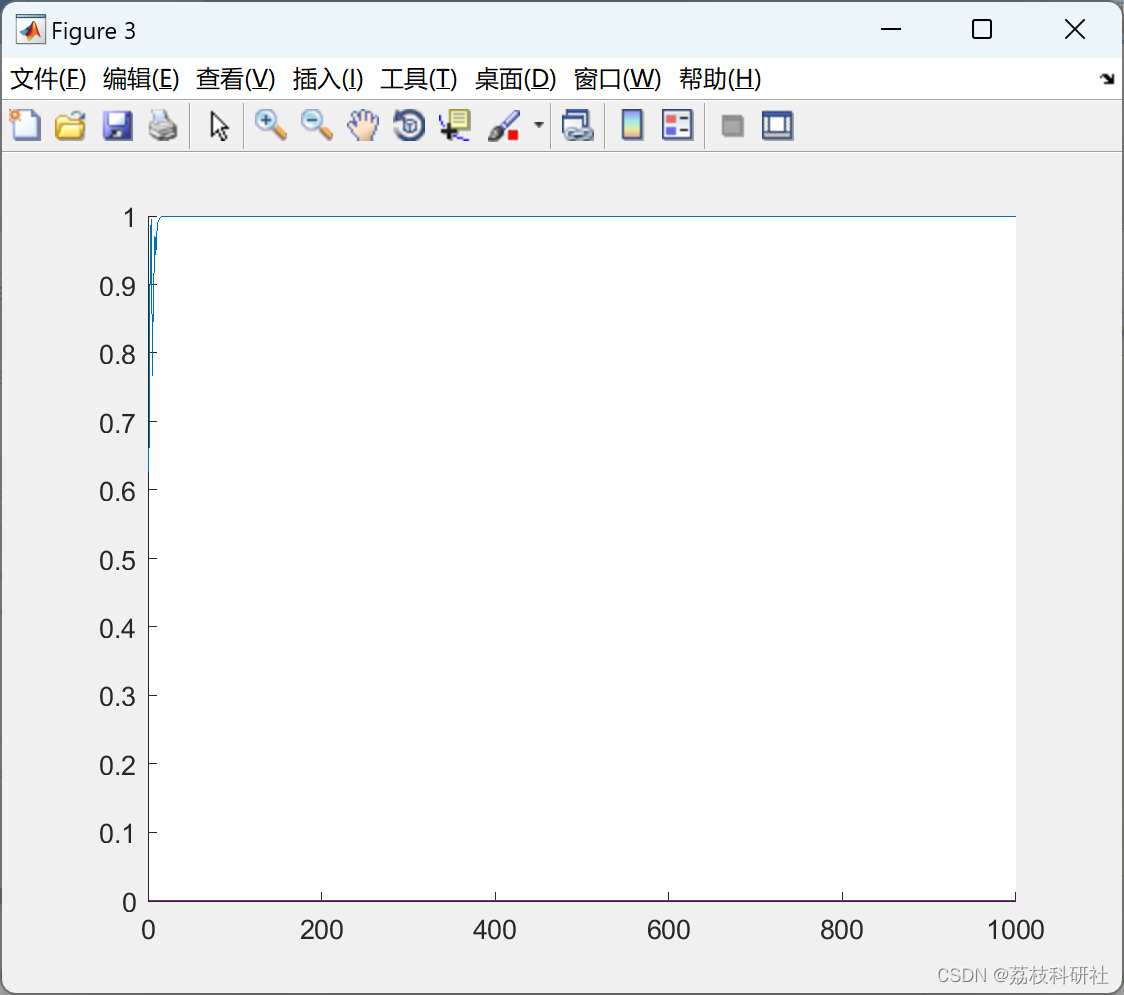

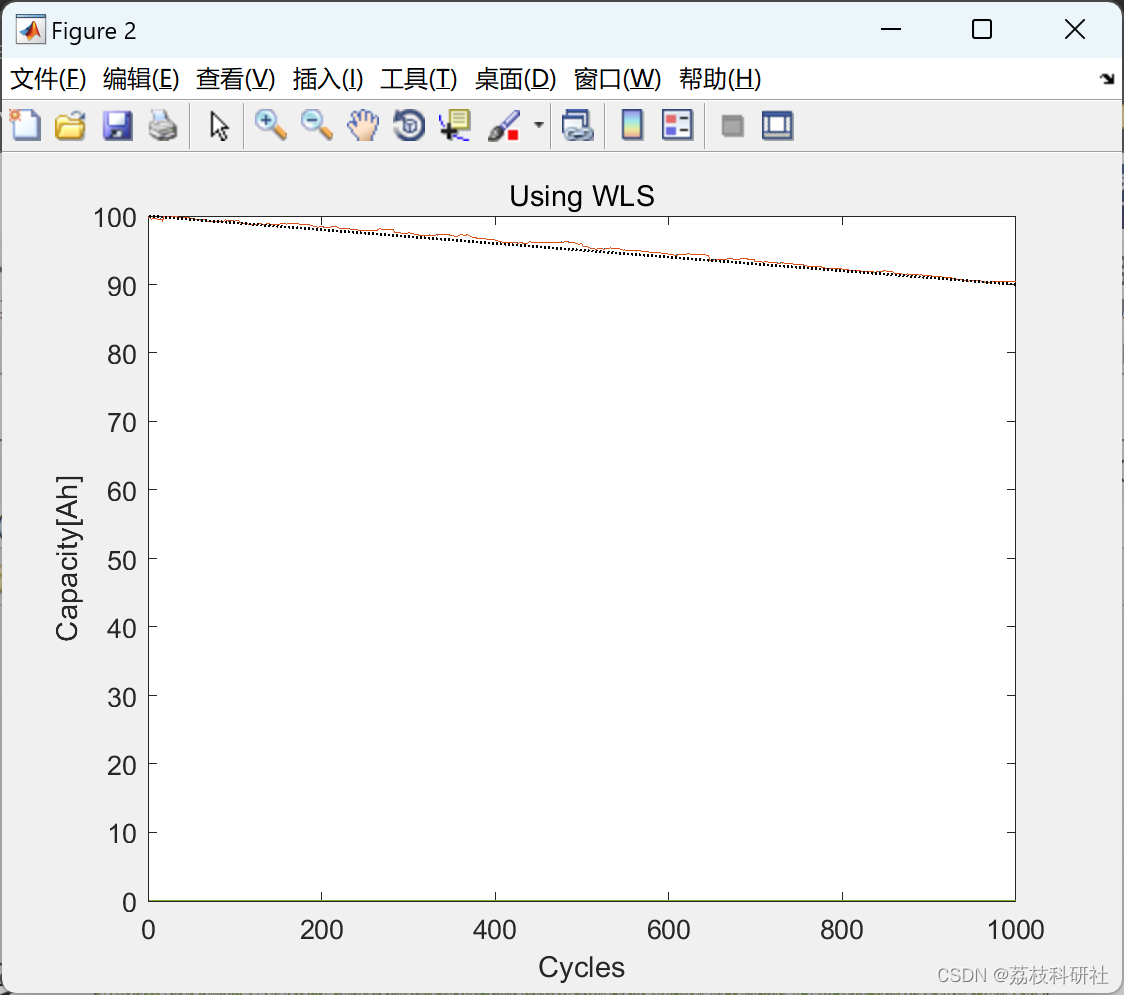
部分代码:
%% Initializing the parameters for our simulation
Q_initial = 100; % true initial capacity [Ah]
I_max = 5*Q_initial; % must be able to measure current up to +/- maxI
I_sensor_bit = 2^10; % 10-bit precision on current sensor (number of combinations)
slope = -0.01; % rate of change of capacity
Q_nom = .99*Q_initial; % nominal capacity
SoC_max = 0.8; % max change in SOC between capacity estimates
SoC_min = -SoC_max; % min change in SOC (signed)
mode = 0.5; sigma = 0.6; % The mode and standard deviation of the measurement updates
socnoise = 0.01; % standard deviation of SOC estimates
gamma = 0.98; % forgetting factor (Range Between 0.9 -0.99 depending on the use case)
%% Computing the simulated data sets
n = 1000; % number of data points to use in computations/plots
Qreal = (Q_initial+slope*(1:n))'; % simulated true capacity as it (possibly) changes over time
x = ((SoC_max-SoC_min)*rand(n,1)+SoC_min); % simulated true change in SOC between measurements (z2-z1)
y = Qreal.*x; % true accumulated ampere hours over that interval
%% Add in some noise to both variables. (Generate Lognormal Random Number)
binsize = 2*I_max/I_sensor_bit;
mu = log(mode)+sigma^2;
m = 3600*lognrnd(mu,sigma,n,1);
del_y = binsize*sqrt(m/12)/3600; % the standard deviation of y (Current measurement noise)
del_x = socnoise*ones(n,1); % the standard deviation of x (SoC estimation noise)
%% Simulated Measured add the deviation (noise)
x = x + del_x.*randn(n,1); % add noise to true change in SOC
y = y + del_y.*randn(n,1); % add noise to accumulated ampere hours
%% To show the effect of using simple linear regression
figure(1);
clf
plot(abs(y)/abs(x));
title("Using regular regression");
xlabel('Cycles');
ylabel('Capacity[Ah]');
%% kick off the algorithm with the measured parameters and the variance of the measurements (SD^2)
SigmaY = del_y.^2;
SigmaX = del_x.^2;
measX = x;
measY = y;
%% AWLTS Start
Qhat = zeros(length(measX),4); SigmaQ = Qhat; Fit = Qhat;
K = sqrt(SigmaX(1)/SigmaY(1));
% Initialize some variables used for the recursive methods.
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
•[1] Plett, G.L.,"Recursive Approximate Weighted Total Least Squares Estimation of Battery Cell Total Capacity" Journal of Power Sources 196(4), 2011
•[2] Devie, Arnaud, George Baure, and Matthieu Dubarry. 2018. "Intrinsic Variability in the Degradation of a Batch of Commercial 18650 Lithium-Ion Cells" Energies 11, no. 5: 1031.