python求解一阶线性偏微分方程的通解举例
Python求解偏微分方程也是其一个应用方面,下面举例说明。
一、问题:
求一阶线性偏微分方程
x
∂
f
(
x
,
y
)
∂
x
−
y
∂
f
(
x
,
y
)
∂
y
+
y
2
f
(
x
,
y
)
=
y
2
x\frac{{\partial f(x,y)}}{{\partial x}} - y\frac{{\partial f(x,y)}}{{\partial y}} + {y^2}f(x,y) = {y^2}
x∂x∂f(x,y)−y∂y∂f(x,y)+y2f(x,y)=y2
的通解。
二、求解代码
import sympy as sp
sp.var('x,y') #定义符号变量,注意要带上引号
f=sp.Function('f') #定义符号函数
u=f(x,y)
ux=u.diff(x)
uy=u.diff(y)
eq=x*ux-y*uy+(y**2)*u-y**2
sp.pprint(eq) #显示方程
s=sp.pdsolve(eq) #求通解
sp.pprint(s)
三、运行结果
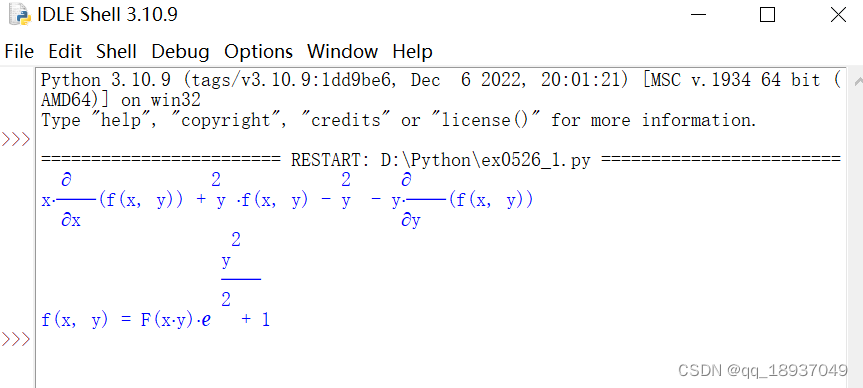
根据运行结果可知,上述问题的通解为
f
(
x
,
y
)
=
F
(
x
y
)
e
y
2
2
+
1
f(x,y) = F(xy){e^{\frac{{{y^2}}}{2}}} + 1
f(x,y)=F(xy)e2y2+1
其中
F
(
⋅
)
F( \cdot )
F(⋅)表示任意函数。