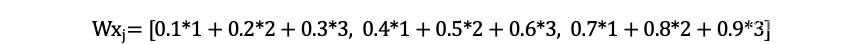权重矩阵更新学习方法概述

1. 参数初始化：

需要对权重矩阵初始化参数（通常使用随机初始化方法，如正态分布或者均匀分布生成随机数）

2. 前向传播：

前向传播中，模型计算权重矩阵和输入数据的结果，得到输出。

3. 误差计算：

根据模型的输出和标签计算误差。在NLP（自然语言处理）任务中，常使用损失函数是交叉墒损失函数。

4. 反向传播：

利用误差更新权重矩阵。通过链式法则（Chain Rule）计算损失函数相对于权重矩阵的梯度。

然后使用梯度下降法（Gradient Descent）或其他优化算法（如Adam）更新权重矩阵

Wq = Wq - learning_rate * dL/dWq

Wk = Wk - learning_rate * dL/dWk

Wv = Wv - learning_rate * dL/dWv

其中learning_rate是学习率，dL/dWq、dL/dWk、dL/dWv分别为损失函数相对于权重矩阵Wq、Wk、Wv的梯度。

5. 迭代训练：

上述步骤完成一个完整的训练迭代。训练过程中，权重矩阵会被不断更新。

迭代训练过程中，模型可以学习到合适的权重矩阵，从而提高模型预测或分类的准确性。

名词说明：

梯度，量化损失函数关于模型参数（权重矩阵）变化时，损失函数的变化。【计算损失函数关于权重矩阵的导数】

举例说明梯度计算（损失函数对于权重矩阵的计算过程）

使用一个简化的神经网络（单层感知机）解决二分类问题。假设输入数据是二维的，因此权重矩阵 W 及偏置项 b 可分别表示为：

W = [w1, w2]

b = b0

对于单个数据点 (x1, x2)，假设真实目标标签为 y_true，模型预测的输出为：

y_pred = sigmoid(w1 * x1 + w2 * x2 + b0)

其中 sigmoid 函数用于将输出转换成概率值。接下来，我们使用二元交叉熵损失（Binary Cross Entropy Loss）：

L(y_true, y_pred) = -[y_true * log(y_pred) + (1 - y_true) * log(1 - y_pred)]

为了更新权重矩阵 W 和偏置项 b，需要计算损失函数 L 关于 W 和 b 的梯度。这里，直接给出梯度的计算结果：

dL/dw1 = (y_pred - y_true) * x1

dL/dw2 = (y_pred - y_true) * x2

dL/db0 = (y_pred - y_true)

现在，我们用一个具体的数据点和参数值来计算梯度。假设：

(x1, x2) = (1.0, 2.0)

y_true = 1

W = [0.5, -0.1]

b0 = 0.2

首先计算 y_pred：

y_pred = sigmoid(0.5 * 1.0 + (-0.1) * 2.0 + 0.2) ≈ 0.509

接下来计算梯度：

dL/dw1 = (0.509 - 1) * 1.0 ≈ -0.491

dL/dw2 = (0.509 - 1) * 2.0 ≈ -0.982

dL/db0 = (0.509 - 1) ≈ -0.491

梯度值告诉我们损失函数在当前参数值下的变化方向。现在根据预设的学习率和梯度更新参数：

learning_rate = 0.1

W_new = [0.5 - 0.1 * (-0.491), -0.1 - 0.1 * (-0.982)] ≈ [0.549, 0.098]

b_new = 0.2 - 0.1 * (-0.491) ≈ 0.249

这个例子展示了如何在具体值条件下计算神经网络中参数的梯度，并用梯度更新参数以减少损失函数值。在实际模型（如多层神经网络）中，这个过程会更复杂，但基本原理是相同的。

构建图结构并提取图特征

代码中图的节点是数据点，边是由K近邻算法（KNN）确定。

具体：

1、找到每个数据点的K个最近邻（KNN）。

计算目标点与邻居点之间的欧氏距离平方，返回其距离矩阵D

通过距离矩阵D，得到距离目标点最近的邻居点。返回值是k个邻居点（特征）和k个邻居点和中心点所连边的索引值idx

2、根据索引值idx，从x（输入）中筛选（找）出其k个邻居点的特征。

import tensorflow as tf


def dyn_dil_get_graph_feature(x, k=16, d=1, use_fsd=False, return_central=True):
    idx = dil_knn(x, k, d, use_fsd)  # 找到每个数据点的K个最近邻；idx是每个数据点与其k个最近邻之间的索引关系。

    # 根据这个索引关系求出从输入特征x中提取出每个点及其邻居点的特征
    if return_central:
        central, neighbors = get_graph_features(x, idx,
                                                True)  # 这里返回的central【shape(batch_size, num_points, k, 3)】和neighbors【shape(batch_size, num_points, k, 3)】。
        return central, neighbors, idx  # 返回中心点特征、邻域点特征、以上两者所连的边的索引值
    else:
        neighbors = get_graph_features(x, idx, False)
    return neighbors, idx


def get_graph_features(x, idx, return_central=True):
    if len(x.get_shape()) > 3:  # 去掉形状为1的维度，使x的shape为(batch_size, num_point, 3)【三维】
        x = tf.squeeze(x, axis=2)
    pc_neighbors = tf.gather_nd(x, idx)  # 根据索引idx从x中提取邻居点的特征（将有idx索引的点从x中提取出来）
    # idx的shape(batch_size, num_point, 2) 表示每个点的k个邻居在x中的位置【二维】即：索引。

    if return_central:

        # 中心点的特征；首先将x在倒数第二个维度上扩展一维，idx.shape[2]=k，，然后将每个点的特征复制k份，使其形状与邻居点特征相同，方便后面运算。
        pc_central = tf.tile(tf.expand_dims(x, axis=-2), [1, 1, idx.shape[2],
                                                          1])  # pc_central的shape和邻居点的shape相同。idx.shape[2]=k。返回的pc_central的shape(batch_size, num_points, k, 3)，即有k份shape(batch_size, num_points, 3)的。
        return pc_central, pc_neighbors
    else:
        return pc_neighbors


def dil_knn(x, k=16, d=1, use_fsd=False):
    if len(x.get_shape()) > 3:
        x = tf.squeeze(x, axis=2)  # 压缩到三维
    idx = knn(x, k=k * d)  # [B N K 2] 使用knn函数找到每个目标点的k*d个邻居点的索引。然后使用d扩展率，筛选出k个邻居点的索引。
    if d > 1:
        if use_fsd:
            idx = idx[:, :, k * (d - 1):k * d, :]
        else:
            idx = idx[:, :, ::d, :]
    return idx


def knn(x, k=16, self_loop=False):
    if len(x.get_shape()) > 3:
        x = tf.squeeze(x, axis=2)  # 维度压缩至3维
    # 找到k+1个邻居的索引idx
    _, idx = knn_point_2(k + 1, x, x, unique=True, sort=True)
    if not self_loop:  # 是否自环，即是否去掉最近的邻居（自己）
        idx = idx[:, :, 1:, :]
    else:
        idx = idx[:, :, 0:-1, :]
    return idx


# KNN的具体实现。 k:邻居点数目；points：目标点；queries是查询点；
def knn_point_2(k, points, queries, sort=True, unique=True):
    with tf.name_scope("knn_point"):
        batch_size = tf.shape(queries)[0]
        point_num = tf.shape(queries)[1]

        D = batch_distance_matrix_general(queries, points)  # 计算查询点和目标点之间的距离，返回距离矩阵。
        if unique:
            prepare_for_unique_top_k(D, points)
        distances, point_indices = tf.nn.top_k(-D, k=k, sorted=sort)  # (N, P, K) 找到距离最近的k个邻居。返回值是k个点的值（负数）和它们的索引。
        batch_indices = tf.tile(tf.reshape(tf.range(batch_size), (-1, 1, 1, 1)), (1, point_num, k, 1))
        indices = tf.concat([batch_indices, tf.expand_dims(point_indices, axis=3)], axis=3)
        return -distances, indices  # 返回目标点和k个最近点的距离和索引值。


# 计算查询点和目标点之间的距离
def batch_distance_matrix_general(A, B):  # A是查询点；B是目标点。

    # A * A表示逐元素相乘。reduce_sum表示求和，axis=2最后一个维度。保持结果的维度数和原始数据相同
    r_A = tf.reduce_sum(A * A, axis=2, keepdims=True)
    r_B = tf.reduce_sum(B * B, axis=2, keepdims=True)
    m = tf.matmul(A, tf.transpose(B, perm=(0, 2, 1)))  # 计算了A点乘B的结果
    D = r_A - 2 * m + tf.transpose(r_B, perm=(0, 2, 1))  # 然后求欧式距离的平方
    return D


def prepare_for_unique_top_k(D, A):
    indices_duplicated = tf.py_func(find_duplicate_columns, [A], tf.int32)
    D += tf.reduce_max(D) * tf.cast(indices_duplicated, tf.float32)

1、计算A和B点之间的欧氏距离，对于两个d维度的向量A和B，他们的欧氏距离平方计算公式为：

||A - B||^2 = (A - B) • (A - B) = A • A - 2A • B + B • B

“•”向量的点积。

A和B的shape和x的shape相同（batch_size, num_points, 3）

A解释：

第一个维度1个元素，第二个维度2个元素，第三个维度3个元素。

第一个维度表示batch_size大小。第二个维度表示num_points大小。第三个维度表示点的x,y,z坐标。A这个Tensor的形状shape(1, 2, 3)。

A =

[

[ [1, 2, 3],

[4, 5, 6] ]

]

B = [[[7, 8, 9], [10, 11, 12]]]

2、点云使用矩阵表示，深度学习中叫做Tensor（张量）。

3、idx如何表示center和neighbor之间边的索引

neighbor的shape(batch_size, num_point, k, 3)

center的shape(batch_size, num_point, k, 3)

idx的shape(batch_size, num_point, k, 2)

例如：idx的shape(i, j, m, : )

表示

第"i"个批处理数据

第"j"个中心点

第"m"个邻居点

表示中心点和邻居点在输入数据中的索引

idx[i, j, m, 1]：表示第i个批处理数据中的第j个中心点的第m个邻居的索引值为1。

对邻居点特征和中心点特征卷积操作

## 1、计算临接点与中心点的特征差异，然后使用卷积层进行处理
message = conv2d(neighbors - central, growth_rate, [1, 1], padding='VALID',
                 scope='message', use_bias=True, activation_fn=None, **kwargs)

## 代表了中心点与其邻近点的相对关系，这可以看作是邻域信息。然后，对这些相对关系进行卷积操作，输出的结果就是新的特征，这个特征融合了中心点及其邻域的信息。
## 2、对中心点特征进行卷积操作

x_center = conv2d(x, growth_rate, [1, 1], padding='VALID',
                  scope='central', use_bias=False, activation_fn=None, **kwargs)

## 将处理过的邻居点特征与中心点特征相加，得到新节点特征
edge_features = x_center + message

1、neighbors - central获取中心点与其邻域点之间的相对关系；对它们的相对关系进行卷积操作。

对每个中心点的邻域信息进行编码：考虑每个中心点的上下文信息，即其邻近的点的特征信息，这是点云数据的局部特征。这个过程的目标是学习到一个能够表达该点以及其周围邻居点特征的新特征。这是通过卷积操作实现的，卷积操作可以看作一种加权平均，使得该中心点的新特征不仅取决于自己，也取决于他周围的点。

"表示中心点从其邻域获得的信息"的意思是，由于卷积操作考虑了该点（中心点）周围的点（邻域）的特征，因此新的特征实际上融合了周围点的信息。因此，该特征表示了该点从其周围邻居获取的信息。

2、对中心点的特征进行提取。

MLPs(多层感知器)

MLP 是一种前馈人工神经网络模型，它将多个网络层（每层都包含一些神经元或节点）连接起来。在 MLP 中，每个神经元的输入都来自前一层的所有神经元，其输出则会传输到下一层的所有神经元，这就是所谓的“全连接”。在这个过程中，每个连接都有相应的权重，这些权重在训练过程中会进行调整。

y = conv2d(y, channels, 1,
           padding='VALID', scope='conv1', **kwargs)

y = conv2d(y, channels, 1,
           padding='VALID', scope='conv2', **kwargs)

y = conv2d(y, channels, 1,
           padding='VALID', scope='conv3', **kwargs)

y = conv2d(y, channels, 1,
           padding='VALID', scope='conv4', **kwargs)

y = conv2d(y, channels * scale, 1,
           padding='VALID', scope='conv5', **kwargs)

对点云数据的卷积

图像卷积

数据形状(batch_size, height, width, channels)，height，width表示图像的高和宽。

图像卷积中，卷积核在图像上滑动，计算卷积核和其覆盖的像素之间的点积，生成新的特征图。这个过程可以理解为局部特征的提取。

点云卷积（专门实现点云卷积的——>动态图卷积【Dynamic Graph Convolution】）

数据形状为(batch_size, num_points, k, 3)，表示有batch_size个批次，每个批次都有num_points个点，每个点有k个邻居，每个邻居有3个坐标值（x, y, z）。

节点特征x在网络中使用矩阵或张量形式表示（图结构也是用这种形式）。在本文中，节点特征的张量x的shape(batch_size, num_points, 3)。

边的信息idx通过邻接矩阵或者边列表表示。在本文中使用KNN搜索得到邻接关系作为边信息idx，idx的这些信息以一个三维张量的形式存储，shape(batch_size, num_points, k)，它存储的是每个点的邻居索引。

节点和边信息共同定义了图结构：节点和边信息存储在不同张量中，节点信息存储在特征矩阵x中，边的信息存储在KNN索引张量idx中。

图卷积（一般的图卷积都会建立邻接矩阵进行计算，这里采用的是KNN****的方法确定每个点的邻居节点，间接的建立邻居关系，可以看作是隐式的邻接矩阵）这种方法计算效率高，因为不需要存储大量的邻接矩阵，适合处理大规模的点云数据，缺点是可能无法捕获到更复杂的图结构信息。

1. 在图卷积中，对于中心节点i，首先找到它的k个最近邻（包括节点自己i）。对于每个邻居节点j，取出他的特征向量x_j，然后用卷积核W与x_j做点乘（或者称为线性变换），得到新的特征向量Wx_j。
2. 对所有的邻居节点，重复操作，然后将所有的Wx_j聚合起来（例如通过求和或者平均），得到中心节点i的新的特征向量。

实例：

卷积核W是3x3的矩阵。

对于节点i的邻居节点j，其特征向量x_j为[1, 2, 3]，则W和x_j的点乘为：