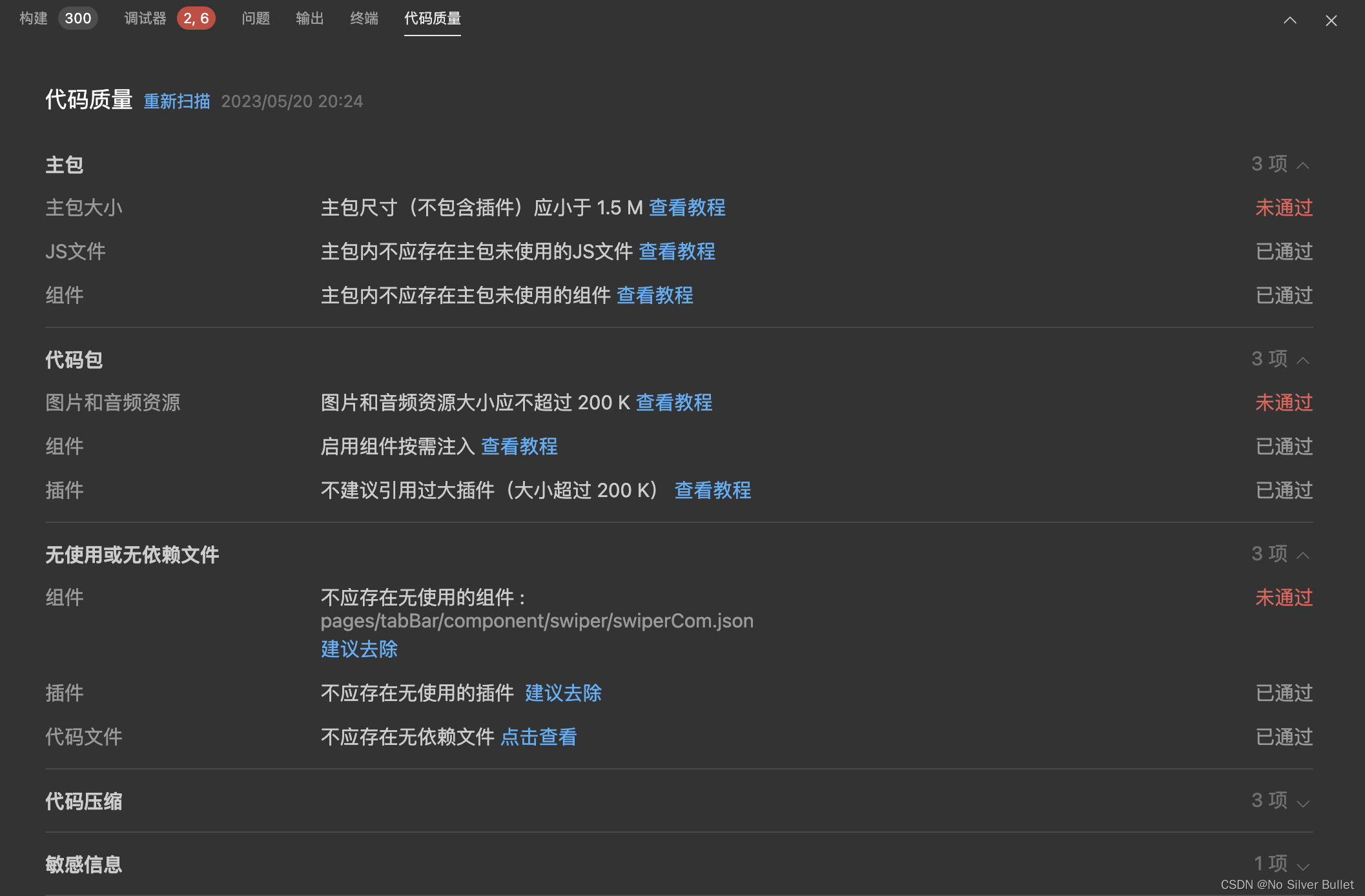
张量的偏微分
张量的一阶微分,定义:
∂
A
∂
A
=
A
,
A
=
∂
A
i
j
∂
A
k
l
(
e
^
i
⨂
e
^
j
⨂
e
^
k
⨂
e
^
l
)
=
δ
i
k
δ
j
l
(
e
^
i
⨂
e
^
j
⨂
e
^
k
⨂
e
^
l
)
=
I
\frac{\partial A}{\partial A} = A_{,A}=\frac{\partial A_{ij}}{\partial A_{kl}}(\hat e_i\bigotimes\hat e_j\bigotimes\hat e_k\bigotimes\hat e_l )\\=\delta_{ik}\delta_{jl}(\hat e_i\bigotimes\hat e_j\bigotimes\hat e_k\bigotimes\hat e_l ) = I
∂A∂A=A,A=∂Akl∂Aij(e^i⨂e^j⨂e^k⨂e^l)=δikδjl(e^i⨂e^j⨂e^k⨂e^l)=I
张量的迹的微分:
∂
T
r
(
A
)
∂
A
=
T
r
(
A
)
,
A
=
∂
A
k
k
∂
A
i
j
(
e
^
i
⨂
e
^
j
)
=
δ
k
i
δ
k
j
(
e
^
i
⨂
e
^
j
)
=
δ
i
j
(
e
^
i
⨂
e
^
j
)
=
1
\frac{\partial Tr(A)}{\partial A} = Tr(A)_{,A}=\frac{\partial A_{kk}}{\partial A_{ij}}(\hat e_i\bigotimes\hat e_j )\\=\delta_{ki}\delta_{kj}(\hat e_i\bigotimes\hat e_j ) = \delta_{ij}(\hat e_i\bigotimes\hat e_j ) = 1
∂A∂Tr(A)=Tr(A),A=∂Aij∂Akk(e^i⨂e^j)=δkiδkj(e^i⨂e^j)=δij(e^i⨂e^j)=1
张量的迹平方的微分:
∂
T
r
(
A
)
2
∂
A
=
2
T
r
(
A
)
T
r
(
A
)
,
A
=
2
T
r
(
A
)
1
\frac{\partial Tr(A)^2}{\partial A} = 2Tr(A)Tr(A)_{,A}=2Tr(A)1
∂A∂Tr(A)2=2Tr(A)Tr(A),A=2Tr(A)1
张量平方的迹的微分:
∂
T
r
(
A
2
)
∂
A
=
∂
A
s
r
A
r
s
∂
A
i
j
(
e
^
i
⨂
e
^
j
)
=
[
A
r
s
∂
A
s
r
∂
A
i
j
+
A
s
r
∂
A
r
s
∂
A
i
j
]
(
e
^
i
⨂
e
^
j
)
=
[
A
r
s
δ
s
i
δ
r
j
+
A
s
r
δ
r
i
δ
s
j
]
(
e
^
i
⨂
e
^
j
)
=
[
A
j
i
+
A
j
i
]
(
e
^
i
⨂
e
^
j
)
=
2
A
j
i
(
e
^
i
⨂
e
^
j
)
=
2
A
T
\frac{\partial Tr(A^2)}{\partial A} =\frac{\partial A_{sr}A_{rs}}{\partial A_{ij}}(\hat e_i\bigotimes\hat e_j )\\=[A_{rs}\frac{\partial A_{sr}}{\partial A_{ij}} + A_{sr}\frac{\partial A_{rs}}{\partial A_{ij}}](\hat e_i\bigotimes\hat e_j )\\ =[A_{rs}\delta_{si}\delta_{rj}+A_{sr}\delta_{ri}\delta_{sj}](\hat e_i\bigotimes\hat e_j )\\= [A_{ji}+A_{ji}](\hat e_i\bigotimes\hat e_j )=2A_{ji}(\hat e_i\bigotimes\hat e_j )=2A^T
∂A∂Tr(A2)=∂Aij∂AsrArs(e^i⨂e^j)=[Ars∂Aij∂Asr+Asr∂Aij∂Ars](e^i⨂e^j)=[Arsδsiδrj+Asrδriδsj](e^i⨂e^j)=[Aji+Aji](e^i⨂e^j)=2Aji(e^i⨂e^j)=2AT
张量立方的迹的微分:
∂
T
r
(
A
3
)
∂
A
=
∂
A
p
q
A
q
r
A
r
p
∂
A
i
j
(
e
^
i
⨂
e
^
j
)
=
[
A
q
r
A
r
p
∂
A
p
q
∂
A
i
j
+
A
p
q
A
r
p
∂
A
q
r
∂
A
i
j
+
A
p
q
A
q
r
∂
A
r
p
∂
A
i
j
]
(
e
^
i
⨂
e
^
j
)
=
[
A
q
r
A
r
p
δ
p
i
δ
q
j
+
A
p
q
A
r
p
δ
q
i
δ
r
j
+
A
p
q
A
q
r
δ
r
i
δ
p
j
]
(
e
^
i
⨂
e
^
j
)
=
[
A
j
r
A
r
i
+
A
p
i
A
j
p
+
A
j
q
A
q
i
]
(
e
^
i
⨂
e
^
j
)
=
3
A
j
r
A
r
i
(
e
^
i
⨂
e
^
j
)
=
3
(
A
2
)
T
\frac{\partial Tr(A^3)}{\partial A} =\frac{\partial A_{pq}A_{qr}A_{rp}}{\partial A_{ij}}(\hat e_i\bigotimes\hat e_j )\\=[A_{qr}A_{rp}\frac{\partial A_{pq}}{\partial A_{ij}} + A_{pq}A_{rp}\frac{\partial A_{qr}}{\partial A_{ij}} + A_{pq}A_{qr}\frac{\partial A_{rp}}{\partial A_{ij}} ](\hat e_i\bigotimes\hat e_j )\\ =[A_{qr}A_{rp}\delta_{pi}\delta_{qj} + A_{pq}A_{rp} \delta_{qi}\delta_{rj} + A_{pq}A_{qr}\delta_{ri}\delta_{pj}](\hat e_i\bigotimes\hat e_j )\\= [A_{jr}A_{ri}+A_{pi}A_{jp}+A_{jq}A_{qi}](\hat e_i\bigotimes\hat e_j )\\ =3A_{jr}A_{ri}(\hat e_i\bigotimes\hat e_j ) =3(A^2)^T
∂A∂Tr(A3)=∂Aij∂ApqAqrArp(e^i⨂e^j)=[AqrArp∂Aij∂Apq+ApqArp∂Aij∂Aqr+ApqAqr∂Aij∂Arp](e^i⨂e^j)=[AqrArpδpiδqj+ApqArpδqiδrj+ApqAqrδriδpj](e^i⨂e^j)=[AjrAri+ApiAjp+AjqAqi](e^i⨂e^j)=3AjrAri(e^i⨂e^j)=3(A2)T
对于对称张量:
∂
T
r
(
C
)
∂
C
=
1
∂
[
T
r
(
C
)
]
2
∂
C
=
2
T
r
(
C
)
1
∂
[
T
r
(
C
2
)
]
∂
C
=
2
C
T
=
2
C
∂
[
T
r
(
C
3
)
]
∂
C
=
3
(
C
2
)
T
=
3
C
2
\frac{\partial Tr(C)}{\partial C} = 1 \\ \frac{\partial [Tr(C)]^2}{\partial C}=2Tr(C) 1 \\ \frac{\partial [Tr(C^2)]}{\partial C}=2C^T=2C \\ \frac{\partial [Tr(C^3)]}{\partial C}=3(C^2)^T=3C^2
∂C∂Tr(C)=1∂C∂[Tr(C)]2=2Tr(C)1∂C∂[Tr(C2)]=2CT=2C∂C∂[Tr(C3)]=3(C2)T=3C2
张量的范数的微分:
∂
∣
∣
C
∣
∣
∂
C
=
∂
C
:
C
∂
C
=
∂
(
T
r
(
C
⋅
C
T
)
)
∂
C
=
∂
T
r
(
C
2
)
∂
C
=
1
2
[
T
r
(
C
2
)
]
−
1
2
[
T
r
(
C
2
)
]
,
C
=
1
2
[
T
r
(
C
2
)
]
−
1
2
2
C
\frac{\partial ||C||}{\partial C}=\frac{\partial \sqrt{C:C}}{\partial C} = \frac{\partial (\sqrt{Tr(C\cdot C^T)})}{\partial C} \\= \frac{\partial \sqrt{Tr(C^2)}}{\partial C}=\frac{1}{2}[Tr(C^2)]^{-\frac{1}{2}}[Tr(C^2)]_{,C}\\=\frac{1}{2}[Tr(C^2)]^{-\frac{1}{2}}2C
∂C∂∣∣C∣∣=∂C∂C:C=∂C∂(Tr(C⋅CT))=∂C∂Tr(C2)=21[Tr(C2)]−21[Tr(C2)],C=21[Tr(C2)]−212C
∂ ∣ ∣ C ∣ ∣ ∂ C = C T r ( C 2 ) = C ∣ ∣ C ∣ ∣ \frac{\partial ||C||}{\partial C} = \frac{C}{\sqrt{Tr(C^2)}}=\frac{C}{||C||} ∂C∂∣∣C∣∣=Tr(C2)C=∣∣C∣∣C
有趣的微分:
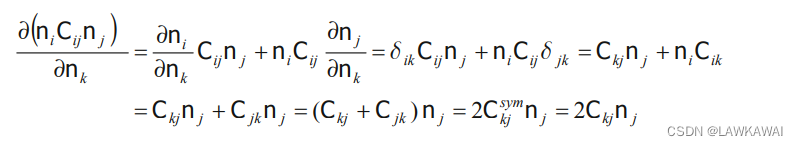
张量的逆的微分:
由于:
∂
1
∂
C
=
∂
(
C
−
1
⋅
C
)
∂
C
=
0
\frac{\partial 1}{\partial C}=\frac{\partial (C^{-1}\cdot C)}{\partial C}= 0
∂C∂1=∂C∂(C−1⋅C)=0
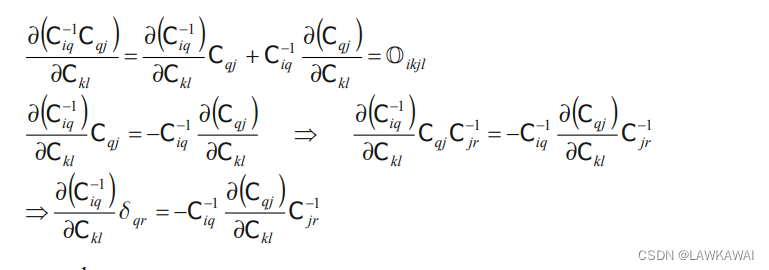
由于:
C
q
j
=
1
2
(
C
q
j
+
C
j
q
)
C_{qj}= \frac{1}{2}(C_{qj}+C_{jq})
Cqj=21(Cqj+Cjq)
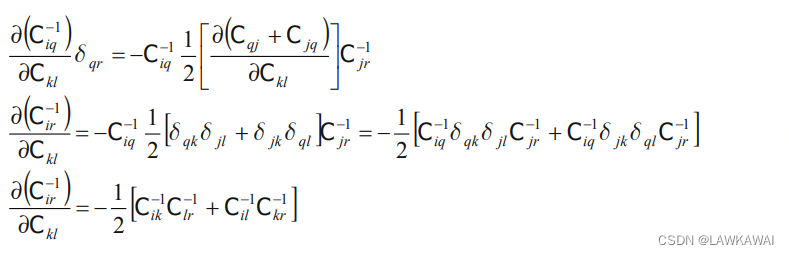
张量形式:
∂
C
−
1
∂
C
=
1
2
[
C
−
1
⨂
‾
C
−
1
+
C
−
1
⨂
‾
C
−
1
]
\frac{\partial C^{-1}}{\partial C}=\frac{1}{2}[C^{-1}\overline \bigotimes C^{-1}+C^{-1} \underline \bigotimes C^{-1}]
∂C∂C−1=21[C−1⨂C−1+C−1⨂C−1]
NOTE: 如果C不是对称的,那么
∂
C
i
q
−
1
∂
C
k
l
δ
q
r
=
−
C
i
q
−
1
∂
C
q
j
∂
C
k
l
C
j
r
−
1
=
−
C
i
q
−
1
δ
q
k
δ
j
l
C
j
r
−
1
=
−
C
i
k
−
1
C
l
r
−
1
\frac{\partial C_{iq}^{-1}}{\partial C_{kl}}\delta_{qr}=-C_{iq}^{-1}\frac{\partial C_{qj}}{\partial C_{kl}}C_{jr}^{-1}=-C_{iq}^{-1}\delta_{qk}\delta_{jl}C_{jr}^{-1} =-C_{ik}^{-1}C_{lr}^{-1}
∂Ckl∂Ciq−1δqr=−Ciq−1∂Ckl∂CqjCjr−1=−Ciq−1δqkδjlCjr−1=−Cik−1Clr−1
不是对称的
不变量的偏微分
I
T
I_T
IT 的微分:
∂
I
T
∂
T
=
∂
T
r
(
T
)
∂
T
=
T
r
(
T
)
,
T
=
1
\frac{\partial I_T}{\partial T}=\frac{\partial Tr(T)}{\partial T} =Tr(T)_{,T}=1
∂T∂IT=∂T∂Tr(T)=Tr(T),T=1
I
I
T
II_T
IIT 的微分:
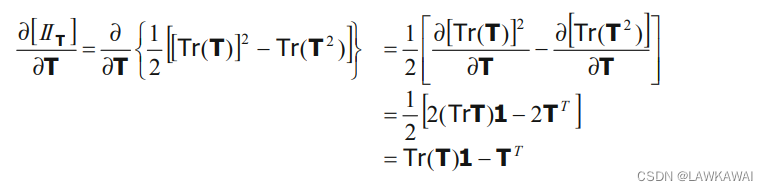
应用Cayley-Hamilton定理:
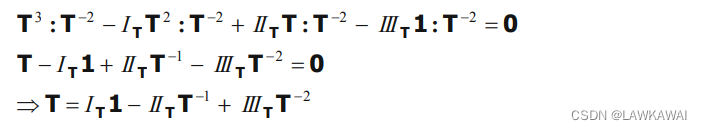
将上式T表达式,代入
I
I
T
II_T
IIT的表达式:
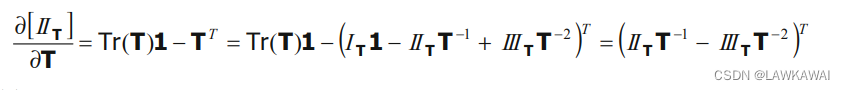
第三不变量
I
I
I
T
III_T
IIIT的微分:

再次应用Cayley-Hamilton定理:
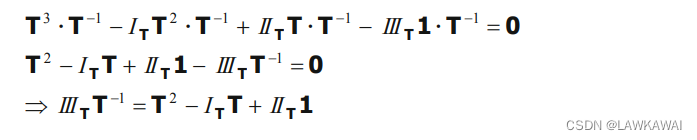
转置:

通过比较,可以求出另一种表示
I
I
I
T
III_T
IIIT的表达式:
∂
I
I
I
T
∂
T
=
(
I
I
I
T
T
−
1
)
T
=
I
I
I
T
T
−
T
\frac{\partial III_T}{\partial T}=(III_T T^{-1})^T=III_T T^{-T}
∂T∂IIIT=(IIITT−1)T=IIITT−T
张量的时间偏导
定义:
D
D
t
T
=
T
˙
D
2
D
t
2
=
T
¨
\frac{D}{Dt}T = \dot T \quad \frac{D^2}{Dt^2}=\ddot T
DtDT=T˙Dt2D2=T¨
张量的行列式的时间偏导:
D
D
t
[
det
T
]
=
D
T
i
j
D
t
c
o
f
(
T
)
\frac{D}{Dt}[\det T] = \frac{DT_{ij}}{Dt}cof (T)
DtD[detT]=DtDTijcof(T)
其中, c o f ( T ) cof (T) cof(T) 是T的余子式, [ c o f [ T i j ] ] T = det ( T ) ( T − 1 ) i j [cof[T_{ij}]]^T = \det (T )(T^{-1})_{ij} [cof[Tij]]T=det(T)(T−1)ij
问题1.38 考虑 J = [ det b ] 1 2 = ( I I I b ) 1 2 J = [\det b]^{\frac{1}{2}} = (III_b)^{\frac{1}{2}} J=[detb]21=(IIIb)21, b b b是二阶对称张量,求出 J J J 和 ln J \ln J lnJ的关于 b b b 的偏导

球张量和偏张量
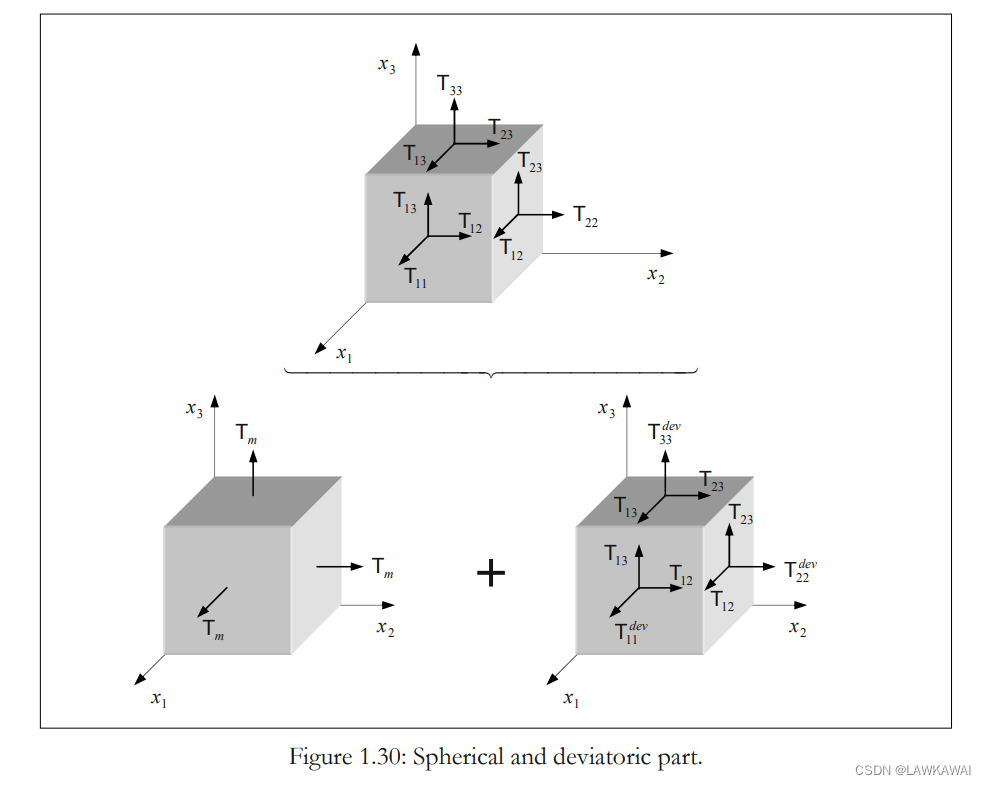
任意一个张量都可以分解成球张量和偏张量:
T
=
T
s
p
h
+
T
d
e
v
=
T
r
(
T
)
3
1
+
T
d
e
v
=
I
T
3
1
+
T
d
e
v
=
T
m
1
+
T
d
e
v
T = T^{sph}+T^{dev}=\frac{Tr(T)}{3}1+T^{dev}=\frac{I_T}{3}1+T^{dev}=T_m1+T^{dev}
T=Tsph+Tdev=3Tr(T)1+Tdev=3IT1+Tdev=Tm1+Tdev
所以,偏张量的定义:
T
d
e
v
=
T
−
T
r
(
T
)
3
1
=
T
−
T
m
1
T^{dev} = T - \frac{Tr(T)}{3}1=T - T_m1
Tdev=T−3Tr(T)1=T−Tm1
由于张量T是对称的,
T
=
T
T
T = T^T
T=TT,所以:
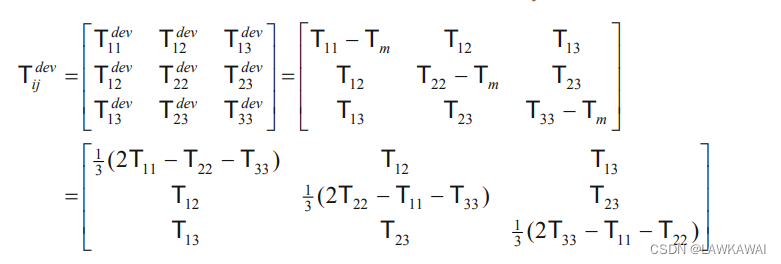
在笛卡尔坐标系表示球张量和偏张量:
接下来介绍根据张量T主不变量的偏张量不变量
偏张量的第一不变量
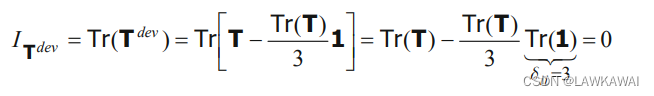
任意偏张量的迹都为0
偏张量的第二不变量
在主空间中,张量T的分量是:
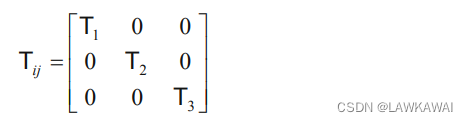
主不变量为:
I
T
=
T
1
+
T
2
+
T
3
;
I
I
T
=
T
1
T
2
+
T
2
T
3
+
T
3
T
1
;
I
I
I
T
=
T
1
T
2
T
3
I_T = T_1+T_2+T_3; \quad II_T = T_1T_2+T_2T_3+T_3T_1; \quad III_T=T_1T_2T_3
IT=T1+T2+T3;IIT=T1T2+T2T3+T3T1;IIIT=T1T2T3
那么偏张量
T
d
e
v
=
T
−
T
m
1
T^{dev} = T - T_m1
Tdev=T−Tm1 在主空间的分量为:
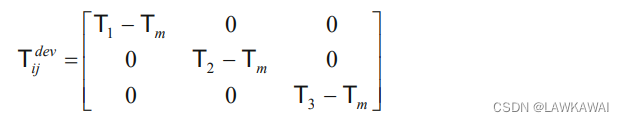
所以,偏张量的第二不变量是:

同样地,也可以用从第二不变量的定义出发证明:
定义:
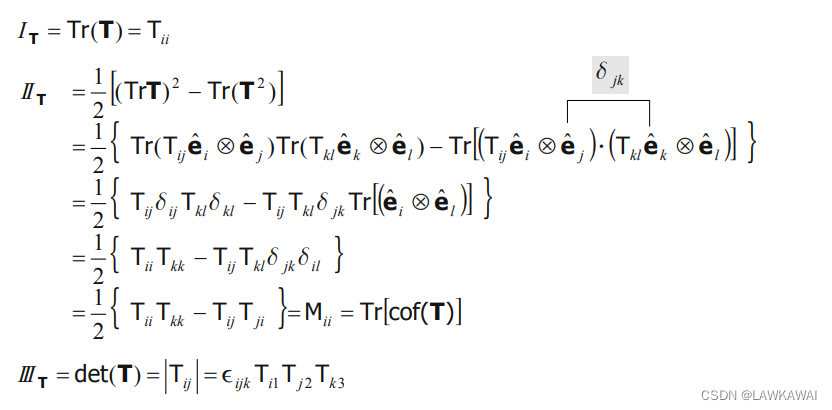
那么偏张量的第二不变量为:
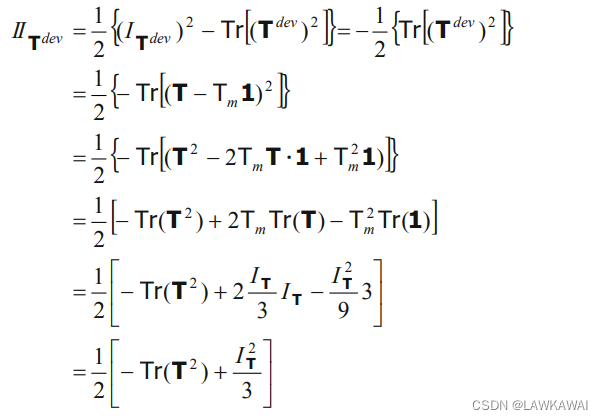
因为不变量不随坐标系的改变而改变,所以在主空间和一般的笛卡尔坐标系中的表达式一样
可以观察到:
T
r
(
T
2
)
=
T
1
2
+
T
2
2
+
T
3
2
=
I
T
2
−
2
I
I
T
Tr(T^2) = T_1^2 + T_2^2 + T_3^2=I_T^2-2II_T
Tr(T2)=T12+T22+T32=IT2−2IIT,(问题1.31),偏张量的第二不变量公式变为用张量T的第一和第二不变量表示的形式:
I
I
T
d
e
v
=
1
2
[
−
I
T
2
+
2
I
I
T
+
I
T
2
3
]
=
1
2
[
2
I
I
T
−
2
I
T
2
3
]
=
1
3
(
3
I
I
T
−
I
T
2
)
II_{T^{dev}}=\frac{1}{2}[-I_T^2+2II_T+\frac{I_T^2}{3}]=\frac{1}{2}[2II_T-\frac{2I_T^2}{3}]=\frac{1}{3}(3II_T-I_T^2)
IITdev=21[−IT2+2IIT+3IT2]=21[2IIT−32IT2]=31(3IIT−IT2)
另一种形式是用偏张量分量表示的形式:
I
I
T
d
e
v
=
−
1
2
T
r
[
(
T
d
e
v
)
2
]
=
−
1
2
T
r
[
(
T
d
e
v
⋅
T
d
e
v
)
]
=
−
1
2
T
d
e
v
⋅
⋅
T
d
e
v
=
−
1
2
T
i
j
d
e
v
T
j
i
d
e
v
II_{T^{dev}}=-\frac{1}{2}Tr[(T^{dev})^2]=-\frac{1}{2}Tr[(T^{dev}\cdot T^{dev})]=-\frac{1}{2}T^{dev}\cdot \cdot T^{dev}=-\frac{1}{2}T_{ij}^{dev}T_{ji}^{dev}
IITdev=−21Tr[(Tdev)2]=−21Tr[(Tdev⋅Tdev)]=−21Tdev⋅⋅Tdev=−21TijdevTjidev
展开,得:
I
I
T
d
e
v
=
−
1
2
[
(
T
11
d
e
v
)
2
+
(
T
22
d
e
v
)
2
+
(
T
33
d
e
v
)
2
+
2
(
T
12
d
e
v
)
2
+
2
(
T
13
d
e
v
)
2
+
2
(
T
23
d
e
v
)
2
]
II_{T^{dev}}=-\frac{1}{2}[(T_{11}^{dev})^2+(T_{22}^{dev})^2+(T_{33}^{dev})^2+2(T_{12}^{dev})^2+2(T_{13}^{dev})^2+2(T_{23}^{dev})^2]
IITdev=−21[(T11dev)2+(T22dev)2+(T33dev)2+2(T12dev)2+2(T13dev)2+2(T23dev)2]
变换一下:
T
11
d
e
v
)
2
+
(
T
22
d
e
v
)
2
+
(
T
33
d
e
v
)
2
=
−
2
I
I
T
d
e
v
−
2
(
T
12
d
e
v
)
2
−
2
(
T
13
d
e
v
)
2
−
2
(
T
23
d
e
v
)
2
T_{11}^{dev})^2+(T_{22}^{dev})^2+(T_{33}^{dev})^2=-2II_{T^{dev}}-2(T_{12}^{dev})^2-2(T_{13}^{dev})^2-2(T_{23}^{dev})^2
T11dev)2+(T22dev)2+(T33dev)2=−2IITdev−2(T12dev)2−2(T13dev)2−2(T23dev)2
另外,在主空间的分量:
I
I
T
d
e
v
=
−
1
2
T
i
j
d
e
v
T
j
i
d
e
v
=
−
1
2
[
(
T
1
d
e
v
)
2
+
(
T
2
d
e
v
)
2
+
(
T
3
d
e
v
)
2
]
II_{T^{dev}}=-\frac{1}{2}T_{ij}^{dev}T_{ji}^{dev}=-\frac{1}{2}[(T_{1}^{dev})^2+(T_{2}^{dev})^2+(T_{3}^{dev})^2]
IITdev=−21TijdevTjidev=−21[(T1dev)2+(T2dev)2+(T3dev)2]
或者:
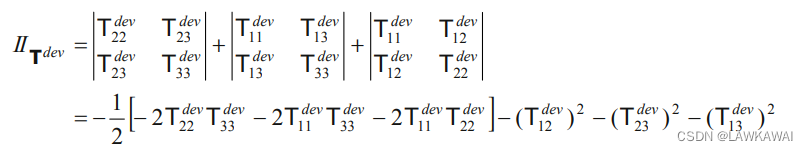
或者:
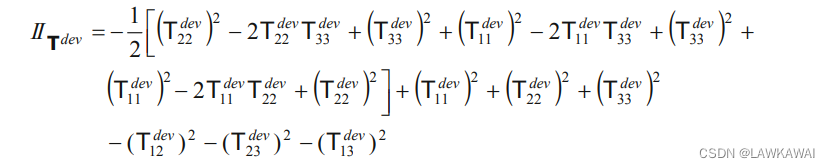
将
I
I
T
d
e
v
=
−
1
2
T
i
j
d
e
v
T
j
i
d
e
v
=
−
1
2
[
(
T
1
d
e
v
)
2
+
(
T
2
d
e
v
)
2
+
(
T
3
d
e
v
)
2
]
II_{T^{dev}}=-\frac{1}{2}T_{ij}^{dev}T_{ji}^{dev}=-\frac{1}{2}[(T_{1}^{dev})^2+(T_{2}^{dev})^2+(T_{3}^{dev})^2]
IITdev=−21TijdevTjidev=−21[(T1dev)2+(T2dev)2+(T3dev)2]代入到以上式子:
I
I
T
d
e
v
=
−
1
6
[
(
T
22
d
e
v
−
T
33
d
e
v
)
2
+
(
T
11
d
e
v
−
T
33
d
e
v
)
2
+
(
T
11
d
e
v
−
T
22
d
e
v
)
2
]
−
(
T
12
d
e
v
)
2
−
(
T
23
d
e
v
)
2
−
(
T
13
d
e
v
)
2
II_{T^{dev}}=-\frac{1}{6}[(T_{22}^{dev}-T_{33}^{dev})^2+(T_{11}^{dev}-T_{33}^{dev})^2+(T_{11}^{dev}-T_{22}^{dev})^2]-(T_{12}^{dev})^2-(T_{23}^{dev})^2-(T_{13}^{dev})^2
IITdev=−61[(T22dev−T33dev)2+(T11dev−T33dev)2+(T11dev−T22dev)2]−(T12dev)2−(T23dev)2−(T13dev)2
如果在主空间,则:
I
I
T
d
e
v
=
−
1
6
[
(
T
2
d
e
v
−
T
3
d
e
v
)
2
+
(
T
1
d
e
v
−
T
3
d
e
v
)
2
+
(
T
1
d
e
v
−
T
2
d
e
v
)
2
]
II_{T^{dev}}=-\frac{1}{6}[(T_{2}^{dev}-T_{3}^{dev})^2+(T_{1}^{dev}-T_{3}^{dev})^2+(T_{1}^{dev}-T_{2}^{dev})^2]
IITdev=−61[(T2dev−T3dev)2+(T1dev−T3dev)2+(T1dev−T2dev)2]
偏张量的第三不变量
偏张量的第三部变量:
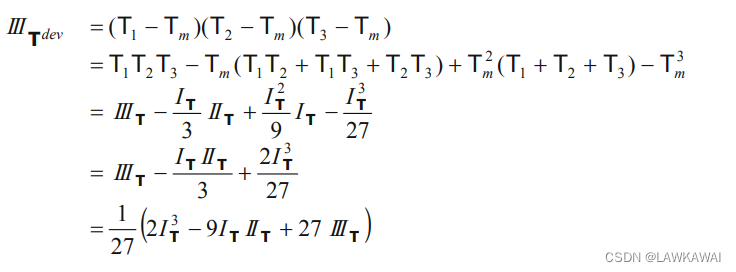
另一个形式:
I
I
I
T
d
e
v
=
T
1
d
e
v
T
2
d
e
v
T
3
d
e
v
=
1
3
T
i
j
d
e
v
T
j
k
d
e
v
T
k
l
d
e
v
III_{T^{dev}}=T_{1}^{dev}T_{2}^{dev}T_{3}^{dev}=\frac{1}{3}T_{ij}^{dev}T_{jk}^{dev}T_{kl}^{dev}
IIITdev=T1devT2devT3dev=31TijdevTjkdevTkldev
问题1.39 σ \sigma σ是对称二阶张量, s = σ d e v s = \sigma^{dev} s=σdev是一个偏张量,证明: s : ∂ s ∂ σ = s s:\frac{\partial s}{\partial \sigma}=s s:∂σ∂s=s,并证明 σ \sigma σ和 σ d e v \sigma^{dev} σdev是同轴张量

参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics

![[Python从零到壹] 六十六.图像识别及经典案例篇之基于机器学习的图像分类](https://img-blog.csdnimg.cn/139d1b6497224e069e1449a76536d36b.png#pic_center)