文章目录
- 集成算法
- 1. 定义
- 2. 具体模型
- 2.1. Bagging
- 2.2. Boosting
- 2.3. Stacking
- 3. 随机森林
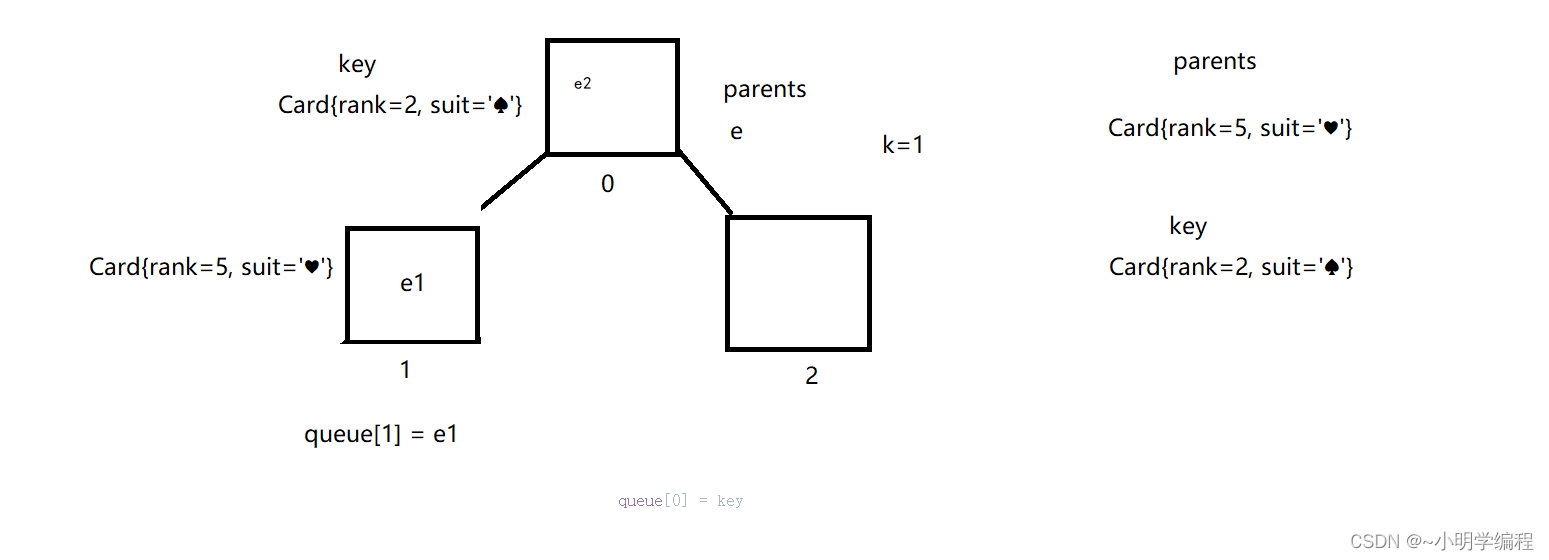
- 3.1. 树模型结构
- 3.2. 随机森林的优点
- 3.3. 分类与回归问题
- 3.4. 树模型个数问题
- 3.5. 参数问题(特征重要性)
- 3.6. 可视化展示问题
- 4. 集成基本思想
- 4.1. 硬投票策略步骤
- 4.2. 软投票策略步骤
- 5. Bagging策略
- 5.1. 策略介绍
- 5.2. 具体实现步骤
- 5.3. 随机森林的特征重要性
- 5.4. mnist数据集特征重要性
- 6. Boosting-提升策略
- 6.1. AdaBoost
- 6.1.1. 模拟流程
- 6.1.2. 工具包实现
- 6.2. Gradient Boosting
- 6.2.1. 模拟流程
- 6.2.2. 工具包实现
- 6.2.3. 提前终止策略
- 7. Stacking策略
- 7.1. 策略介绍
- 7.2. 具体实现步骤
集成算法
1. 定义
将多个分类器集成起来而形成的新的分类算法,主要包括Bagging、Boosting和Stacking三种类别,其中前两种比较常用。
2. 具体模型
2.1. Bagging
-
概述:此类算法中每个模型之间是相互独立的,他们之间的评估结果互不影响,并行训练分类器
-
构建方法: 对于给定的含有n个样本数据集,每次从中抽取某些样本放入到采样集中,然后又将该样本放回到原数据集中,继续进行采样抽取,也就是做有放回抽样,在采样结束后可以根据每个采样集中的样本分别进行对基评估器进行训练。典型的代表就是随机森林算法,随机森林包含两层含义,其中随机的意思是数据采样随机和特征选择随机,采用的是有放回抽样,而森林是把多个决策树放在一起,这样组合起来才能使数据具有更大的随机性。
-
数学表达式:由于样本独立,类似于并行电路,要对多个分类器取平均

2.2. Boosting
-
概述:此类算法是每个模型是相互关联的,后面加入的模型要比之前的模型有更加突出的模型,比较严格,是从弱学习开始加强,通过加权来进行训练,串行训练分类器。
-
构建方法:先反复学习得到一些弱分类器,然后组合这些弱分类器变成一个强分类器,主要包括两个部分,加强模型和向前分步,每一次的分步都要加上之前的所有模型的结果,慢慢叠加,达到最优的效果。典型的代表就是
AdaBoost,Xgboost- AdaBoost:会根据前一次的分类效果调整数据权重,解释来说就是如果某一数据在这次分错了,那么下一次就会被分配更大的权重,最终的结果就是根据自身的准确性来确定各自的权重,再合体。具体工作流程如下图所示,每次都会根据权重重新分配。

- AdaBoost:会根据前一次的分类效果调整数据权重,解释来说就是如果某一数据在这次分错了,那么下一次就会被分配更大的权重,最终的结果就是根据自身的准确性来确定各自的权重,再合体。具体工作流程如下图所示,每次都会根据权重重新分配。
-
数学表达式:每次都要加上之前所有的模型,所以是一个加的运算,然后之后每次加入的模型,都要与前一次的模型进行对比,如果由于之前的模型就加入,否则就舍弃,具体公式如下:

2.3. Stacking
此类算法就是简单的将多个不同的分类模型堆叠在一起(KNN,SVM,RF等),它是分阶段进行的,第一阶段得出各自的结果,第二阶段再用前一阶段结果进行训练,比较耗时,一般不常使用。
3. 随机森林
随机森林属于Bagging类别,构造的树模型由于数据和特征都是随机的,所以构造出来的树模型是不相同的
3.1. 树模型结构

3.2. 随机森林的优点
- 能够处理很高维度的数据,并且不同做特征选择,机器学习的库中有专门的函数针对数据和特征进行分配
- 训练完成后,能够给出哪些特征比较重要
- 容易做并行化方法,速度比较快
- 可以进行可视化展示,便于分析
3.3. 分类与回归问题
对于所有的树模型,分类任务中,求众数就是分类结果;在回归任务中,直接求平均值。
3.4. 树模型个数问题
树模型的个数不是越多越好,由下图可知,随着树模型的增加,准确率提升的比较快,但是当树模型个数到达10以后,可以看出准确率趋于稳定。稳定之后,出现的上下浮动的现象是因为构建决策树的时候,它们之间相互独立,很难保证每一棵树加起来之后都会比原来的结果要好,所以,要控制树模型的数量。

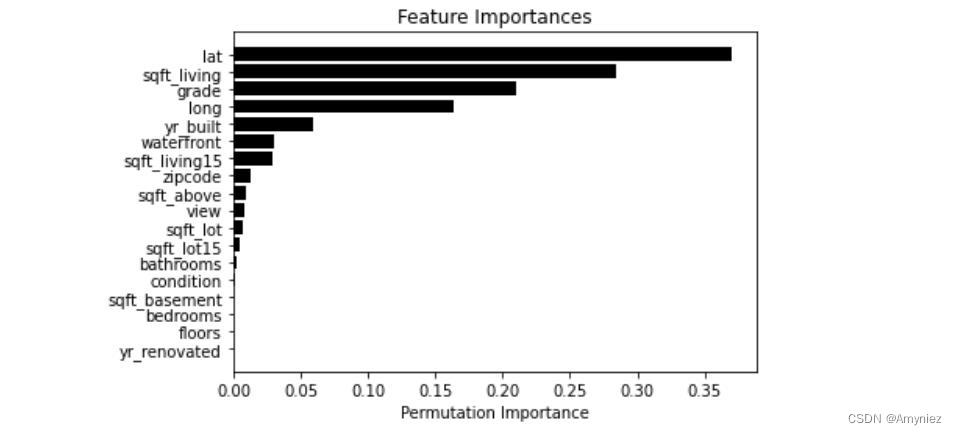
3.5. 参数问题(特征重要性)
特征重要性就是每个特征的重要程度,哪些特征被多次使用,哪些特征就重要,如下图所示有一个feature importance。

下面来举一个计算的例子,使用错误率来衡量特征的重要程度,下图有四个特征,分别为A、B、C、D,本例子就是对比B特征的重要程度,所以引入噪音点B',两组数据经过相同的训练模型,分别得到对应的错误率err1和err2,下面分析错误率:
- 当
err1≈err2的时候,说明有没有特征B,得到的结果类似,说明B不重要 - 当
err1<<err2的时候,说明把B特征数据打乱后,与原数据有很大的差别,说明B很重要 - 一般情况下不会出现
err1>>err2的情况

3.6. 可视化展示问题
当使用树模型时,可以非常清晰地得到整个分裂过程,方便进行可视化分析 , 如下图所示,可视化展示很强。

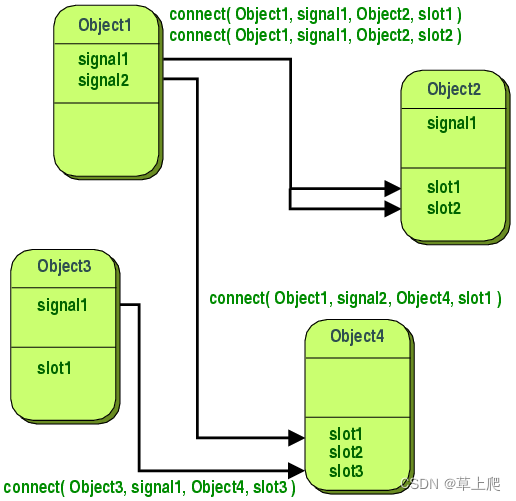
4. 集成基本思想
训练时用多种分类器一起完成同一个任务,如下图所示,对于同一个数据集,使用逻辑回归算法、SVM算法、随机森林算法等等共同完成一个任务。

测试时对测试样本分别通过不同的分类器,汇总最后的结果
4.1. 硬投票策略步骤
- 导入基本数据处理、画图、警告处理的包
import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)
- 导入数据集分割和生成数据集的包
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_moons
# n_numbers: 生成样本数量;
# noise: 默认是false,数据集是否加入高斯噪声;
# random_state: 生成随机种子,给定一个int型数据,能够保证每次生成数据相同
X,y = make_moons(n_samples=500,noise=0.3,random_state=42)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=42)
- 画图展示
plt.plot(X[:,0][y==0],X[:,1][y==0],'ro',alpha = 0.7)
plt.plot(X[:,0][y==0],X[:,1][y==1],'gs',alpha = 0.7)
-
数据集效果展示

-
硬投票操作:直接用类别值,少数服从多数
# 导入随机森林和投票器模块
from sklearn.ensemble import RandomForestClassifier,VotingClassifier
# 导入逻辑回归模块
from sklearn.linear_model import LogisticRegression
# 导入SVM模块
from sklearn.svm import SVC
# 实例化
rnd_clf = RandomForestClassifier(random_state = 42)
log_clf = LogisticRegression(random_state = 42)
svm_clf = SVC(random_state = 42)
# 进行投票
voting_clf = VotingClassifier(estimators = [('rf',rnd_clf),('lr',log_clf),('svc',svm_clf)],voting='hard')
- 实验结果评估
# 导入精确度模块
from sklearn.metrics import accuracy_score
# 分类别进行测试
for clf in (rnd_clf,log_clf,svm_clf,voting_clf):
clf.fit(X_train,y_train)
y_pred = clf.predict(X_test)
print(clf.__class__.__name__,accuracy_score(y_test,y_pred))
结果:
RandomForestClassifier 0.896
LogisticRegression 0.864
SVC 0.896
VotingClassifier 0.912分析:从实验结果可以看出,硬投票比单个的实验结果的准确率要高一些
4.2. 软投票策略步骤
软投票策略的前4个步骤与硬投票相同,不再赘述。
- 软投票操作:各自分类器的概率值进行加权平均
# 导入随机森林和投票器模块
from sklearn.ensemble import RandomForestClassifier,VotingClassifier
# 导入逻辑回归模块
from sklearn.linear_model import LogisticRegression
# 导入SVM模块
from sklearn.svm import SVC
# 实例化
rnd_clf = RandomForestClassifier(random_state = 42)
log_clf = LogisticRegression(random_state = 42)
svm_clf = SVC(random_state = 42,probability=True)
# 进行投票
voting_clf = VotingClassifier(estimators = [('rf',rnd_clf),('lr',log_clf),('svc',svm_clf)],voting='soft')
- 实验结果评估
# 导入精确度模块
from sklearn.metrics import accuracy_score
# 分类别进行测试
for clf in (rnd_clf,log_clf,svm_clf,voting_clf):
clf.fit(X_train,y_train)
y_pred = clf.predict(X_test)
print(clf.__class__.__name__,accuracy_score(y_test,y_pred))
结果:
RandomForestClassifier 0.896
LogisticRegression 0.864
SVC 0.896
VotingClassifier 0.92分析:从实验结果可以看出,软投票比单个的实验结果的准确率要高一些。同时对比硬投票与软投票,软投票结果比硬投票要好一点
5. Bagging策略
5.1. 策略介绍
- 首先对训练数据集进行多次采样,保证每次得到的采样数据都是不同的
- 分别训练多个模型,例如树模型
- 预测时需要得到所有模型结果再进行集成

5.2. 具体实现步骤
- 导包进行训练
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
# base_estimator: 选择的基本估计量的类型
# n_estimators: 基本估计量的个数,此处为决策树的数量
# max_samples: 每次从数据集中取出的样本的个数
# bootstrap: 每次取的样本是随机的
# n_jobs: 使用所有处理器
# random_state: 生成随机种子,给定一个int型数据,能够保证每次生成数据相同
bag_clf = BaggingClassifier(
base_estimator = DecisionTreeClassifier(),
n_estimators = 500,
max_samples = 100,
bootstrap = True,
n_jobs = -1,
random_state = 42
)
# 进行训练
bag_clf.fit(X_train,y_train)
# 进行预测
y_pred = bag_clf.predict(X_test)
- 得到Bagging策略的准确度
# 使用Bagging方法获得的精确度
accuracy_score(y_test,y_pred)
## 结果: 0.904
- 选择树模型进行对比
# 对比实验,使用树模型获得的准确度
tree_clf = DecisionTreeClassifier(random_state = 42)
tree_clf.fit(X_train,y_train)
y_pred_tree = tree_clf.predict(X_test)
accuracy_score(y_test,y_pred_tree)
## 结果: 0.856
- 绘制决策边界
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf,X,y,axes=[-1.5,2.5,-1,1.5],alpha=0.5,contour =True):
x1s=np.linspace(axes[0],axes[1],100)
x2s=np.linspace(axes[2],axes[3],100)
# 绘制棋盘
x1,x2 = np.meshgrid(x1s,x2s)
# 拼接
X_new = np.c_[x1.ravel(),x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1,x2,y_pred,cmap = custom_cmap,alpha=0.3)
if contour:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1,x2,y_pred,cmap = custom_cmap2,alpha=0.8)
# 画出原始数据
plt.plot(X[:,0][y==0],X[:,1][y==0],'ro',alpha = 0.7)
plt.plot(X[:,0][y==0],X[:,1][y==1],'gs',alpha = 0.7)
plt.axis(axes)
plt.xlabel('x1')
plt.ylabel('x2',rotation=0)
- 画图展示
plt.figure(figsize = (12,5))
plt.subplot(121)
plot_decision_boundary(tree_clf,X,y)
plt.title('Decision Tree')
plt.subplot(122)
plot_decision_boundary(bag_clf,X,y)
plt.title('Decision Tree With Bagging')
-
效果展示

-
结果分析
实验从两个角度进行对比,步骤2与步骤3从准确率的角度对Bagging策略与基本决策树模型进行对比,可以看出Bagging策略得到的准确率为
0.904,而决策树模型得到的准确率为0.856,可以看出Bagging策略优于决策树模型;步骤4,5,6是绘制边界的角度进行对比,由上图所示,左侧是进行决策树算法得到的结果图,右侧是进行Bagging策略得到的结果图,从右图可知,拟合的曲线相对稳定,平稳的曲线才是我们想要的,左侧的决策树模型有过拟合的现象。 -
bagging自带的结果验证
袋外数据验证,袋外的意思就是从原始数据集中抽取训练集之后,剩余的数据集,这是bagging策略自带的一种评价指标
bag_clf = BaggingClassifier(
base_estimator = DecisionTreeClassifier(),
n_estimators = 500,
max_samples = 100,
bootstrap = True,
n_jobs = -1,
random_state = 42,
oob_score = True
)
# 进行训练
bag_clf.fit(X_train,y_train)
# 使用袋外数据进行验证结果
bag_clf.oob_score_
## 结果: 0.9253333333333333
5.3. 随机森林的特征重要性
-
导包并训练
根据随机森林里面特有的特征
feature_importances_进行计算
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
iris = load_iris()
rf_clf = RandomForestClassifier(n_estimators = 500,n_jobs = -1)
rf_clf.fit(iris['data'],iris['target'])
for name,score in zip(iris['feature_names'],rf_clf.feature_importances_):
print(name,score)
- 画图展示
import matplotlib
import random
import matplotlib.pyplot as plt
name = ['sepal length', 'sepal width', 'petal length', 'petal width']
data = [0.10,0.02,0.43,0.45]
fig, ax = plt.subplots()
b = ax.barh(range(len(name)), data, color='#6699CC')
for rect in b:
w = rect.get_width()
ax.text(w, rect.get_y()+rect.get_height()/2, '%.2f' %float(w), ha='left', va='center')
ax.set_yticks(range(len(name)))
ax.set_yticklabels(name)
plt.xticks(())
plt.title('Characteristics of importance', loc='center', fontsize='16',fontweight='bold', color='green')
plt.show()
-
效果展示
下图的结果表明,
petal width和petal length是很重要的特征

5.4. mnist数据集特征重要性
- 导包获取数据集并进行训练
from sklearn.datasets import fetch_mldata
from sklearn.ensemble import RandomForestClassifier
mnist = fecch_mldata('MNIST original')
rf_clf = RandomForestClassifier(n_estimators=500,n_jobs=-1)
rf_clf.fit(mnist['data'],mnist['target'])
- 画图展示
def plot_digit(data):
image = data.reshape(28,28)
plt.imshow(image,cmap=matplotlib.cm.hot)
plt.axis('off')
plot_digit(rf_clf.feature_importances_)
char = plt.colorbar(ticks=[rf_clf.feature_importances_.min(),rf_clf.feature_importances_.max()])
char.ax.set_yticklabels(['Not important','Very important'])
-
效果展示
mnist数据集中只有中间才是数字,其他都是白边, 数值特征在什么位置重要,用热度图进行展示,热度图一般与图像数据结合使用。

6. Boosting-提升策略
6.1. AdaBoost
策略介绍:在原始数据集中直接进行预测,观察预测不好的点,然后提升它们的权重,再前一次的基础上进行预测,各个结果值按照不同的权重配比,组成最后的结果。

6.1.1. 模拟流程
(以SVM分类器为例来演示AdaBoost的基本策略)
from sklearn.svm import SVC
# 计算样本个数
m = len(X_train)
plt.figure(figsize=(12,4))
# 不同的调节力度对结果的影响,用学习率来表示,然后画两个图来进行对比实验
for subplot,learning_rate in ((121,1),(122,0.5)):
# 开始的时候权重相同
sample_weights = np.ones(m)
plt.subplot(subplot)
# 构建5次,得到5个模型,然后把五个模型串在一起
for i in range(5):
svm_clf = SVC(kernel = 'rbf',C=0.05,random_state=42)
# sample_weight: 当前样本的权重项
svm_clf.fit(X_train,y_train,sample_weight=sample_weights)
y_pred = svm_clf.predict(X_train)
sample_weights[y_pred != y_train] *= (1+learning_rate)
plot_decision_boundary(svm_clf,X,y,alpha=0.7)
plt.title('learning_rate = {}'.format(learning_rate))
if subplot == 121:
plt.text(-0.7, -0.65, "1", fontsize=14)
plt.text(-0.6, -0.10, "2", fontsize=14)
plt.text(-0.5, 0.10, "3", fontsize=14)
plt.text(-0.4, 0.55, "4", fontsize=14)
plt.text(-0.3, 0.90, "5", fontsize=14)
plt.show()
效果展示:

6.1.2. 工具包实现
(使用sklearn工具包实现)
from sklearn.ensemble import AdaBoostClassifier
ada_clf = AdaBoostClassifier(
base_estimator = DecisionTreeClassifier(max_depth = 1),
n_estimators = 200,
learning_rate = 0.5,
random_state = 42
)
ada_clf.fit(X_train,y_train)
plot_decision_boundary(ada_clf,X,y)
效果展示

6.2. Gradient Boosting
6.2.1. 模拟流程
- 创造数据
# 先做数据集
np.random.seed(42)
X = np.random.rand(100,1) - 0.5
y = 3*X[:,0]**2 + 0.05*np.random.randn(100)
- 导包并进行训练
from sklearn.tree import DecisionTreeRegressor
# 第一次训练
tree_reg1 = DecisionTreeRegressor(max_depth = 2)
tree_reg1.fit(X,y)
# 第二次训练
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth = 2)
tree_reg2.fit(X,y2)
# 第三次训练
y3 = y2 - tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth = 4)
tree_reg3.fit(X,y3)
# 第四次训练
y4 = y3 - tree_reg3.predict(X)
tree_reg4 = DecisionTreeRegressor(max_depth = 2)
tree_reg4.fit(X,y4)
- 画图展示
def plot_predictions(regressors, X, y, axes, label=None, style="g-", data_style="b.", data_label=None):
x1 = np.linspace(axes[0], axes[1], 500)
y_pred = sum(regressor.predict(x1.reshape(-1, 1)) for regressor in regressors)
plt.plot(X[:, 0], y, data_style, label=data_label)
plt.plot(x1, y_pred, style, linewidth=2, label=label)
if label or data_label:
plt.legend(loc="upper center", fontsize=16)
plt.axis(axes)
plt.figure(figsize=(11,15))
plt.subplot(421)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h_1(x_1)$", style="r-", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Residuals and tree predictions", fontsize=16)
plt.subplot(422)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1)$", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Ensemble predictions", fontsize=16)
plt.subplot(423)
plot_predictions([tree_reg2], X, y2, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_2(x_1)$", style="r-", data_style="k+", data_label="Residuals")
plt.ylabel("$y - h_1(x_1)$", fontsize=16)
plt.subplot(424)
plot_predictions([tree_reg1, tree_reg2], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1)$")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.subplot(425)
plot_predictions([tree_reg3], X, y3, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_3(x_1)$", style="r-", data_style="k+")
plt.ylabel("$y - h_1(x_1) - h_2(x_1)$", fontsize=16)
plt.xlabel("$x_1$", fontsize=16)
plt.subplot(426)
plot_predictions([tree_reg1, tree_reg2, tree_reg3], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1) + h_3(x_1)$")
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.subplot(427)
plot_predictions([tree_reg4], X, y4, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_4(x_1)$", style="r-", data_style="k+")
plt.ylabel("$y - h_1(x_1) - h_2(x_1) - h_3(x_1)$", fontsize=16)
plt.xlabel("$x_1$", fontsize=16)
plt.subplot(428)
plot_predictions([tree_reg1, tree_reg2, tree_reg3,tree_reg4], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1) + h_3(x_1) + h_4(x_1)$")
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.show()
-
效果展示

分析:图1(从上到下,从左至右排序)是第一棵树,蓝色的点为数据集,红色线条为预测结果;图2代表一个树的集成,与左侧图一样;图3是在图1的基础上进行预测的结果,在位置0的时候没有参差值,0的两侧是在图1的基础上的参差值,是第一次预测过程中效果不好的点;图4是集成两颗树的结果;图5是在前两次的基础上进行预测的结果,并且调整树的深度为4,得到的预测结果;图6是三棵树的集成结果;图7的预测结果看出,基本没有参差值,此时可以达到很好的预测结果;图8为4棵树的集成结果,可以看出,基本符合预期的结果。
6.2.2. 工具包实现
- 导包并训练
from sklearn.ensemble import GradientBoostingRegressor
gbrt = GradientBoostingRegressor(
max_depth = 2,
n_estimators = 3,
# 代表每个数占的权重
learning_rate = 1,
random_state = 42
)
gbrt.fit(X,y)
- 进行对比实验
# 对比实验一: 调整权重
gbrt_slow_1 = GradientBoostingRegressor(
max_depth = 2,
n_estimators = 3,
# 代表每个数占的权重
learning_rate = 0.1,
random_state = 42
)
gbrt_slow_1.fit(X,y)
# 对比实验二: 调整推进阶段的数量
gbrt_slow_2 = GradientBoostingRegressor(
max_depth = 2,
n_estimators = 200,
# 代表每个数占的权重
learning_rate = 0.1,
random_state = 42
)
gbrt_slow_2.fit(X,y)
- 画图展示
plt.figure(figsize=(16,4))
plt.subplot(131)
plot_predictions([gbrt],X,y,axes = [-0.5,0.5,-0.1,0.8],label = 'Ensemble predictions')
plt.title('learning_rate = {},n_estimators = {}'.format(gbrt.learning_rate,gbrt.n_estimators))
plt.subplot(132)
plot_predictions([gbrt_slow_1],X,y,axes = [-0.5,0.5,-0.1,0.8],label = 'Ensemble predictions')
plt.title('learning_rate = {},n_estimators = {}'.format(gbrt_slow_1.learning_rate,gbrt_slow_1.n_estimators))
plt.subplot(133)
plot_predictions([gbrt_slow_2],X,y,axes = [-0.5,0.5,-0.1,0.8],label = 'Ensemble predictions')
plt.title('learning_rate = {},n_estimators = {}'.format(gbrt_slow_2.learning_rate,gbrt_slow_2.n_estimators))
-
效果展示

分析:上面三个图构成两组对比实验,由图1和图2可知,在要执行的推进阶段的数量相同的前提下,学习率越大反而越好,出现这种情况的原因是推进阶段的数量太少;由第2个图和第3个图的对比中,在学习率(代表每个数占的权重)相同的前提下,推进的数量越多,效果越好。因此,推进数量应当适当的大一点,学习率应适当小一点。
6.2.3. 提前终止策略
- 导包并训练
# 导入均方误差
from sklearn.metrics import mean_squared_error
X_train,X_val,y_train,y_val = train_test_split(X,y,random_state = 49)
gbrt = GradientBoostingRegressor(max_depth = 2,
n_estimators = 120,
random_state = 42
)
gbrt.fit(X_train,y_train)
# 获取错误点
errors = [mean_squared_error(y_val,y_pred) for y_pred in gbrt.staged_predict(X_val)]
# 找出出错前预测结果最好的点
bst_n_estimators = np.argmin(errors)
# 用最好的点进行预测
gbrt_best = GradientBoostingRegressor(max_depth = 2,
n_estimators = bst_n_estimators,
random_state = 42
)
gbrt_best.fit(X_train,y_train)
min_error = np.min(errors)
- 画图展示
plt.figure(figsize = (11,4))
plt.subplot(121)
plt.plot(errors,'b.-')
plt.plot([bst_n_estimators,bst_n_estimators],[0,min_error],'k--')
plt.plot([0,120],[min_error,min_error],'k--')
plt.axis([0,120,0,0.01])
plt.title('Val Error')
plt.subplot(122)
plot_predictions([gbrt_best],X,y,axes=[-0.5,0.5,-0.1,0.8])
plt.title('Best Model(%d trees)'%bst_n_estimators)
-
效果展示

分析:当树的数量达到55的时候,达到最好的效果,之后就开始回弹。
-
终止策略实现
# warm_start在上一次的基础上进行叠加,速度会快一点
gbrt = GradientBoostingRegressor(max_depth = 2,
random_state = 42,
warm_start =True
)
error_going_up = 0
min_val_error = float('inf')
for n_estimators in range(1,120):
gbrt.n_estimators = n_estimators
gbrt.fit(X_train,y_train)
y_pred = gbrt.predict(X_val)
val_error = mean_squared_error(y_val,y_pred)
if val_error < min_val_error:
min_val_error = val_error
error_going_up = 0
else:
error_going_up +=1
if error_going_up == 5:
break
- 输出结果
print (gbrt.n_estimators)
## 结果: 61
分析:从最佳树的数量55开始,计算5个树,如果之后加入的5个树全部使原数据回弹,则往前推5个就找到了最佳树的个数。
7. Stacking策略
7.1. 策略介绍
Stacking策略分两个阶段进行,第一个阶段是选择不同的分类器,得到多个预测值,第二个阶段根据每个预测值的权重进行集成,如下图所示。

训练示意图:

7.2. 具体实现步骤
- 加载数据集
from sklearn.datasets import fetch_mldata
from sklearn.model_selection import train_test_split
mnist = fetch_mldata('MNIST original')
X_train_val, X_test, y_train_val, y_test = train_test_split(mnist.data, mnist.target, test_size=10000, random_state=42)
X_train, X_val, y_train, y_val = train_test_split(X_train_val, y_train_val, test_size=10000, random_state=42)
- 导入各种分类器并生成分类器的对象,最后进行集成
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.svm import LinearSVC
from sklearn.neural_network import MLPClassifier
random_forest_clf = RandomForestClassifier(random_state=42)
extra_trees_clf = ExtraTreesClassifier(random_state=42)
svm_clf = LinearSVC(random_state=42)
mlp_clf = MLPClassifier(random_state=42)
estimators = [random_forest_clf, extra_trees_clf, svm_clf, mlp_clf]
- 对每个分类器进行训练
for estimator in estimators:
print("Training the", estimator)
estimator.fit(X_train, y_train)
- 对分类器进行预测
X_val_predictions = np.empty((len(X_val), len(estimators)), dtype=np.float32)
for index, estimator in enumerate(estimators):
X_val_predictions[:, index] = estimator.predict(X_val)
- 第二阶段集成分类器并进行训练
rnd_forest_blender = RandomForestClassifier(n_estimators=200, oob_score=True, random_state=42)
rnd_forest_blender.fit(X_val_predictions, y_val)
- 观察预测结果
rnd_forest_blender.oob_score_
![[附源码]java毕业设计代驾服务系统](https://img-blog.csdnimg.cn/44e472bf9d3e40c9af315cc2991b0afe.png)